bzoj4518 [Sdoi2016]征途

4518: [Sdoi2016]征途

Time Limit: 10 Sec  Memory Limit: 256 MB
Submit: 1812  Solved: 1006
[Submit][Status][Discuss]

Description

Pine开始了从S地到T地的征途。

从S地到T地的路可以划分成n段，相邻两段路的分界点设有休息站。

Pine计划用m天到达T地。除第m天外，每一天晚上Pine都必须在休息站过夜。所以，一段路必须在同一天中走完。

Pine希望每一天走的路长度尽可能相近，所以他希望每一天走的路的长度的方差尽可能小。

帮助Pine求出最小方差是多少。

设方差是v，可以证明，v×m^2是一个整数。为了避免精度误差，输出结果时输出v×m^2。

Input

第一行两个数 n、m。

第二行 n 个数，表示 n 段路的长度

Output

 一个数，最小方差乘以 m^2 后的值

Sample Input

5 2
1 2 5 8 6

Sample Output

36

HINT

1≤n≤3000,保证从 S 到 T 的总路程不超过 30000

Source

鸣谢Menci上传

分析：挺有心机的一道题.

　　　这道题知道了两点就能做出来了：1.最后的答案乘上m^2不是为了避免精度误差.  2.走的路的长度的平均值是确定的.

　　　令sum[i]表示前i个点d[i]的前缀和，v = sum[n] / m,实际上就是平均值.  方差是 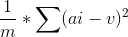，乘上m^2不就把m给消掉了嘛.

把v 拆成 sum[n] / m然后将式子展开，可以得到最终的答案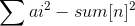：,那么题目就变成了分出m段路，使得所有路的长度的平方和最小，典型的斜率优化.

　　　f[i][j] = min{f[k][j - 1] + (sum[i] - sum[k]) ^ 2}.

　　　有时候题目将最后的答案进行特殊处理也是一种提示，不要被题面给迷惑了！ 这种题就是先写式子然后化简拆项，看每一项应该怎么求.

 

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;
const ll maxn = 3010,inf = 1e17;
ll n,m,a[maxn],sum[maxn],f[maxn],g[maxn],ans = inf,l,r,q[maxn];

ll K(ll i)
{
    return -2 * sum[i];
}

ll B(ll i)
{
    return g[i] + sum[i] * sum[i];
}

ll Y(ll i,ll j)
{
    return K(i) * sum[j] + B(i);
}

bool cmp(ll y1,ll y2,ll y3)
{
    ll temp1 = (K(y1) - K(y3)) * (B(y2) - B(y1));
    ll temp2 = (K(y1) - K(y2)) * (B(y3) - B(y1));
    return temp1 >= temp2;
}

int main()
{
    scanf("%lld%lld",&n,&m);
    for (ll i = 1; i <= n; i++)
        scanf("%lld",&a[i]);
    for (ll i = 1; i <= n; i++)
        sum[i] = sum[i - 1] + a[i];
    for (ll i = 1; i <= n; i++)
        g[i] = inf;
    ans = inf;
    g[0] = 0;
    for (ll i = 1; i <= m; i++)
    {
        l = r = 0;
        for (ll j = 1; j <= n; j++)
        {
            while (l < r && Y(q[l],j) >= Y(q[l + 1],j))
                l++;
            f[j] = Y(q[l],j) + sum[j] * sum[j];
            while (l < r && cmp(j,q[r - 1],q[r]))
                r--;
            q[++r] = j;
        }
        for (ll j = 1; j <= n; j++)
            g[j] = f[j];
    }
    ans = g[n];
    printf("%lld\n",ans * m - sum[n] * sum[n]);

    return 0;
}