bzoj1597 [Usaco2008 Mar]土地购买

1597: [Usaco2008 Mar]土地购买

Time Limit: 10 Sec  Memory Limit: 162 MB
Submit: 5716  Solved: 2160
[Submit][Status][Discuss]

Description

农夫John准备扩大他的农场,他正在考虑N (1 <= N <= 50,000) 块长方形的土地. 每块土地的长宽满足(1 <= 宽 <

= 1,000,000; 1 <= 长 <= 1,000,000). 每块土地的价格是它的面积,但FJ可以同时购买多快土地. 这些土地的价

格是它们最大的长乘以它们最大的宽, 但是土地的长宽不能交换. 如果FJ买一块3x5的地和一块5x3的地,则他需要

付5x5=25. FJ希望买下所有的土地,但是他发现分组来买这些土地可以节省经费. 他需要你帮助他找到最小的经费.

Input

* 第1行: 一个数: N

* 第2..N+1行: 第i+1行包含两个数,分别为第i块土地的长和宽

Output

* 第一行: 最小的可行费用.

Sample Input

4
100 1
15 15
20 5
1 100
输入解释:
共有4块土地.

Sample Output

500
FJ分3组买这些土地:
第一组:100x1,
第二组1x100,
第三组20x5 和 15x15 plot.
每组的价格分别为100,100,300, 总共500.

分析：挺好的一道题！

　　　土地的长和宽是两个影响因素，一起处理很难,先尝试消除一个因素的影响：按照长从大到小排序.这样就能够写一个dp转移方程

f(i) = min{max{w[k]} * l[j + 1] + f(j)}  (j+1≤k≤i). O(n^2)的复杂度，难以通过本题.

　　　尝试一下优化，这个似乎可以决策单调性搞一搞？推一推有关w的式子发现并不一定成立. 怎么办？换个角度.

　　　将长看作纵坐标，宽看作横坐标，往平面直角坐标系上投影. 对于一个点(x,y)，如果还存在一个点(x',y'),使得x' ≥ x,y'≥ y,那么点(x,y)就没有存在的价值了. 可以发现，,宽也是有序的了!

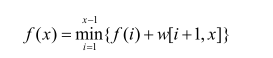　　　得到新的dp式子：f(i) = min{w[i] * l[j + 1] + f(j)},显然这是可以决策单调性优化的，对应经典模型：.套个模板就好啦.

 

　　　本题有两个转化，第一个转化还是挺容易看出来的，第二个转化不是很容易想到:两个相互关联的变量可以投影到坐标系上.要多积累这种思想！

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;


typedef long long ll;

const ll maxn = 50010;

struct node
{
    ll a,b;
}e[maxn],s[maxn];

struct node2
{
    ll l,r,p;
}q[maxn];

int n;
ll maxx,tot,f[maxn],cur,top;

bool cmp(node a,node b)
{
    if(a.a == b.a)
        return a.b > b.b;
    return a.a > b.a;
}

ll calc(ll x,ll y)
{
    return f[x] + s[x + 1].a * s[y].b;
}

int find(node2 temp,int pos)
{
    ll l = temp.l,r = temp.r,ans = temp.r + 1;
    while (l <= r)
    {
        ll mid = (l + r) >> 1;
        if (calc(pos,mid) < calc(temp.p,mid))
        {
            ans = mid;
            r = mid - 1;
        }
        else
            l = mid + 1;
    }
    return ans;
}

void solve()
{
    node2 temp;
    temp.l = 1;
    temp.r = tot;
    temp.p = 0;
    q[++top] = temp;
    cur = 1;
    for (int i = 1; i <= tot; i++)
    {
        if (q[cur].r < i)
            cur++;
        f[i] = calc(q[cur].p,i);
        while (1)
        {
            node2 temp = q[top];
            if (calc(i,temp.r) < calc(temp.p,temp.r))
            {
                if (calc(i,temp.l) < calc(temp.p,temp.l))
                {
                    top--;
                    continue;
                }
                else
                {
                    int x = find(temp,i);
                    q[top].r = x - 1;
                    break;
                }
            }
            else
                break;
        }
        if (q[top].r < tot)
        {
            node2 temp;
            temp.l = q[top].r + 1;
            temp.r = tot;
            temp.p = i;
            q[++top] = temp;
        }
    }
}

int main()
{
    scanf("%d",&n);
    for(int i = 1; i <= n; i++)
        scanf("%lld%lld",&e[i].a,&e[i].b);
    sort(e + 1,e + 1 + n,cmp);
    for (int i = 1; i <= n; i++)
        if (e[i].b > maxx)
        {
            maxx = e[i].b;
            s[++tot] = e[i];
        }
    solve();
    printf("%lld\n",f[tot]);

    return 0;
}