Codeforces Round #461 (Div. 2)
应该算是第二次正式打cf了,打的特别揪心的一场比赛.比赛时间非常晚,凌晨一点左右,整个人迷迷糊糊的.
比赛时很快就切了T1,T2快打完的时候系统告诉我T1被hack掉了......尼玛,T1都能被hack掉.之后T2也被切掉了,希望不要被hack.
看T3,一眼感觉不可做,但是打表找了找规律,发现数据范围其实应该特别小,因为有了T1的教训,我特地特判了边界,过了pretest,心想这次应该不会被hack了.
结果我打T4的时候,尼玛T3又被hack了,还是同一个人.这个人做完前3题后就一直hack别人,把整个房间的人都给hack干净了......
T4好不容易打出来,自己编了几组数据测了程序没问题,就交上去了,结果没过pretest......绝望,看着还有20分钟,都已经凌晨3点了,感觉D题刚不出了,关上电脑去睡觉.
在床上还感到非常不爽,这次铁定要掉rating了,又感到非常疑惑,为什么T4会错?在脑海里YY了几组数据,发现我的贪心策略有漏洞!于是赶紧爬起来打开电脑改程序.还剩下三分钟了,这鬼编译器还打不开.终于在最后1min我改完交上去了,眼看着它过了pretest,最后关头锁上了.其实内心也没抱多大希望,之前那个老是hack我的大哥和我是房间里唯二的做出这道题的人,他肯定会疯狂hack我,而我是最后关头想出来了贪心策略,很有可能是错的.唉,算了,先睡觉吧.
结果,T4 A了......还涨rating了......看了看分数,如果那两道题没有被hack掉我现在rating很有可能会涨100+(毕竟第二次打嘛).
Imp likes his plush toy a lot.

Recently, he found a machine that can clone plush toys. Imp knows that if he applies the machine to an original toy, he additionally gets one more original toy and one copy, and if he applies the machine to a copied toy, he gets two additional copies.
Initially, Imp has only one original toy. He wants to know if it is possible to use machine to get exactly x copied toys and y original toys? He can't throw toys away, and he can't apply the machine to a copy if he doesn't currently have any copies.
The only line contains two integers x and y (0 ≤ x, y ≤ 10^9) — the number of copies and the number of original toys Imp wants to get (including the initial one).
Print "Yes", if the desired configuration is possible, and "No" otherwise.
You can print each letter in arbitrary case (upper or lower).
6 3
Yes
4 2
No
1000 1001
Yes
In the first example, Imp has to apply the machine twice to original toys and then twice to copies.
题目大意:一个真实的玩具可以变出另一个真实的玩具和复制的玩具,一个复制的玩具可以变成两个额外的复制的玩具,你一开始有一个真实的玩具,现在给出最后复制的玩具和真实的玩具的数量,问有没有可能达到这种局面.
分析:变出真实的玩具和复制的玩具的两个过程是独立的.分两个过程判断一下就好了.需要特别注意的是x,y有可能等于0,初始时y=1,需要特判y=0和y=1的情况.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; ll a,b; bool flag = true; int main() { cin >> a >> b; b--; if (b < 0 || b >= a + 1) flag = false; if (b == 0 && a != 0) flag = false; a -= b; if (a % 2 != 0) flag = false; if (flag) puts("Yes"); else puts("No"); return 0; }
Imp is in a magic forest, where xorangles grow (wut?)

A xorangle of order n is such a non-degenerate triangle, that lengths of its sides are integers not exceeding n, and the xor-sum of the lengths is equal to zero. Imp has to count the number of distinct xorangles of order n to get out of the forest.
Formally, for a given integer n you have to find the number of such triples (a, b, c), that:
- 1 ≤ a ≤ b ≤ c ≤ n;
![]() , where
, where ![]() denotes the bitwise xor of integers x and y.
denotes the bitwise xor of integers x and y.- (a, b, c) form a non-degenerate (with strictly positive area) triangle.
The only line contains a single integer n (1 ≤ n ≤ 2500).
Print the number of xorangles of order n.
6
1
10
2
The only xorangle in the first sample is (3, 5, 6).
题目大意:给定n,问是否存在3个数满足a <= b <= c <= n,a xor b xor c=0且a,b,c是三角形的三条边长.
分析:挺水的一道题,稍微懂点异或的性质就能做了.枚举b,c,因为第二个条件,一个数异或自己等于0,那么a就等于b xor c,最后判断一下a,b,c是否能组成三角形就可以了.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; int n,ans; int main() { scanf("%d",&n); for (int i = 1; i <= n; i++) { for (int j = 1; j <= i; j++) { int temp = i ^ j; if (temp > j || temp > i) continue; if (temp + j <= i) continue; ans++; } } printf("%d\n",ans); return 0; }
Imp is watching a documentary about cave painting.

Some numbers, carved in chaotic order, immediately attracted his attention. Imp rapidly proposed a guess that they are the remainders of division of a number n by all integers i from 1 to k. Unfortunately, there are too many integers to analyze for Imp.
Imp wants you to check whether all these remainders are distinct. Formally, he wants to check, if all 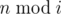 , 1 ≤ i ≤ k, are distinct, i. e. there is no such pair (i, j) that:
, 1 ≤ i ≤ k, are distinct, i. e. there is no such pair (i, j) that:
- 1 ≤ i < j ≤ k,
![]() , where
, where ![]() is the remainder of division x by y.
is the remainder of division x by y.
The only line contains two integers n, k (1 ≤ n, k ≤ 1018).
Print "Yes", if all the remainders are distinct, and "No" otherwise.
You can print each letter in arbitrary case (lower or upper).
4 4
No
5 3
Yes
In the first sample remainders modulo 1 and 4 coincide.
题目大意:给定n和k,问当i取1到k中的所有数时,n % i的结果是不是都不同.
分析:数据范围这么大看似不可做,其实打个表就能发现真实的数据范围根本就没这么大. 如果数n % i的结果都不同,它要满足什么条件呢?
n % 1 == 0
n % 2 == 1
n % 3 == 2
n % 4 == 3
......
n % i == i - 1
当i到一定大小的时候n就会变得特别大,i是1e18时,n早就超过1e18了.所以可以得出结论,这道题直接暴力就好了......暴力枚举i判断,最后肯定是i比较小就会返回false.
我脑抽特判了一下边界,结果被hack掉了......事实上这个枚举就包含了所有情况.经验不足啊QAQ.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; ll n,k,maxx; bool vis[3000000]; bool solve(ll x,ll y) { memset(vis,0,sizeof(vis)); for (int i = 1; i <= y; i++) { ll temp = x % i; if (vis[temp]) return false; vis[temp] = 1; } return true; } int main() { cin >> n >> k; bool flag = solve(n,k); if (flag) puts("Yes"); else puts("No"); return 0; }
Pushok the dog has been chasing Imp for a few hours already.

Fortunately, Imp knows that Pushok is afraid of a robot vacuum cleaner.
While moving, the robot generates a string t consisting of letters 's' and 'h', that produces a lot of noise. We define noise of string t as the number of occurrences of string "sh" as a subsequence in it, in other words, the number of such pairs (i, j), that i < j and 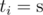 and
and 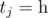 .
.
The robot is off at the moment. Imp knows that it has a sequence of strings ti in its memory, and he can arbitrary change their order. When the robot is started, it generates the string t as a concatenation of these strings in the given order. The noise of the resulting string equals the noise of this concatenation.
Help Imp to find the maximum noise he can achieve by changing the order of the strings.
The first line contains a single integer n (1 ≤ n ≤ 105) — the number of strings in robot's memory.
Next n lines contain the strings t1, t2, ..., tn, one per line. It is guaranteed that the strings are non-empty, contain only English letters 's' and 'h' and their total length does not exceed 105.
Print a single integer — the maxumum possible noise Imp can achieve by changing the order of the strings.
4
ssh
hs
s
hhhs
18
2
h
s
1
The optimal concatenation in the first sample is ssshhshhhs.
题目大意:给n个只由s和h组成的字符串,你可以改变它们拼接的顺序,求最后拼接起来子串"sh"的数目的最大值(可以不连续).
分析:第一个想法是dp.但是n和字符串长度都很大,想不到怎么设计状态.既然数据范围这么大,很容易就能想到贪心,但是具体要怎么贪呢?
首先只由s组成的串肯定是要放到最前面的,h要放到最后面.然后我一开始的想法把s多的串放在前面,h多的串放在后面,一样多的放在中间,事实上这个贪心策略是矛盾的,如果串a的s和h都比串b多,那么a和b要怎么放呢.后来我YY了一个例子:sssshhhh,ssh.这时ssh放在前面更优.为什么呢?ssh这个串中s的数量/h的数量大于sssshhhh的,也就是说我们只要比较s和h数量的比值就可以了.那如果比值一样怎么办?这时无论位置如何答案总是不变的,因为两内项之积等于两外项之积.
需要注意的是只包含s和h的串要单独处理,即用两个变量记录s和h的数量.除法比较大小可以转化为乘法比较大小.
因为需要统计所有串s和h的数量,我怕10w*10w会超时,用了getchar,虽然感觉没什么用......最后我发现我看错题目了,是串的总长加起来不超过10w......
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; const ll maxn = 100010; struct node { ll x,y; ll ans; } e[maxn]; char ch; ll n,cnt,cnts,cnth; ll ans; bool cmp(node a,node b) { if (a.x * b.y != a.y * b.x) return a.x * b.y > a.y * b.x; } int main() { cin >> n; getchar(); for (ll i = 1; i <= n; i++) { ll cnta = 0,cntb = 0; ll temp = 0; while (ch = getchar()) { if (ch == '\n') break; if (ch == 's') cnta++; else { temp += cnta; cntb++; } } if (cntb == 0) cnts += cnta; else if (cnta == 0) cnth += cntb; else { e[++cnt].x = cnta; e[cnt].y = cntb; e[cnt].ans = temp; } } sort(e + 1,e + 1 + cnt,cmp); for (ll i = 1; i <= cnt; i++) { ans += e[i].ans; ans += cnts * e[i].y; cnts += e[i].x; } ans += cnts * cnth; cout << ans << endl; return 0; }
Apart from plush toys, Imp is a huge fan of little yellow birds!

To summon birds, Imp needs strong magic. There are n trees in a row on an alley in a park, there is a nest on each of the trees. In the i-th nest there are ci birds; to summon one bird from this nest Imp needs to stay under this tree and it costs him costi points of mana. However, for each bird summoned, Imp increases his mana capacity by B points. Imp summons birds one by one, he can summon any number from 0 to ci birds from the i-th nest.
Initially Imp stands under the first tree and has W points of mana, and his mana capacity equals W as well. He can only go forward, and each time he moves from a tree to the next one, he restores X points of mana (but it can't exceed his current mana capacity). Moving only forward, what is the maximum number of birds Imp can summon?
The first line contains four integers n, W, B, X (1 ≤ n ≤ 103, 0 ≤ W, B, X ≤ 109) — the number of trees, the initial points of mana, the number of points the mana capacity increases after a bird is summoned, and the number of points restored when Imp moves from a tree to the next one.
The second line contains n integers c1, c2, ..., cn (0 ≤ ci ≤ 104) — where ci is the number of birds living in the i-th nest. It is guaranteed that 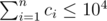 .
.
The third line contains n integers cost1, cost2, ..., costn (0 ≤ costi ≤ 109), where costi is the mana cost to summon a bird from the i-th nest.
Print a single integer — the maximum number of birds Imp can summon.
2 12 0 4
3 4
4 2
6
4 1000 10 35
1 2 4 5
1000 500 250 200
5
2 10 7 11
2 10
6 1
11
In the first sample base amount of Imp's mana is equal to 12 (with maximum capacity also equal to 12). After he summons two birds from the first nest, he loses 8 mana points, although his maximum capacity will not increase (since B = 0). After this step his mana will be 4 of 12; during the move you will replenish 4 mana points, and hence own 8 mana out of 12 possible. Now it's optimal to take 4 birds from the second nest and spend 8 mana. The final answer will be — 6.
In the second sample the base amount of mana is equal to 1000. The right choice will be to simply pick all birds from the last nest. Note that Imp's mana doesn't restore while moving because it's initially full.
题目大意:Imp想要召唤最多数量的鸟,有n个鸟巢,只能从前往后走,已知第i个鸟巢有ci只鸟,召唤一只鸟要花费cost_i能量,每召唤一只鸟能量的上限就会增加B,从第i个鸟巢走向第i+1个鸟巢能量会增加x,但是不能超过上限,问最多能召唤多少只鸟.
分析:一道挺好的题.
一眼就能看出这是一个背包问题,但是容量会变?而且第二维存容量也存不下啊?感觉一脸不可做.但是它要求的只是最多能召唤多少只鸟,鸟的数量相对于容量而言是比较小的,所以我们可以把状态的第二维设置为鸟的数量.那么f[i][j]表示前i个鸟巢中,召唤j只鸟后剩下的能量.最后只需要从大到小枚举鸟的数量,看f[n][i]是否≥0即可.就是把求解最优性问题变成判定性问题,把状态多,结果小的dp状态的状态和结果互换,常用的技巧......
状态转移方程很容易就能得到了:f[i][j] = max(f[i][j],min(f[i][j - k] + x,w + (j - k) * b) - cost * k).中间取min是判断是否达到容量的上限.
这类问题做得还不是很熟练啊,一些基本的dp转化都没想出来QAQ.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; const ll maxn = 1010; ll n; ll w,b,x,c[maxn],cost[maxn],f[maxn][10010],ans,sum,summ[maxn]; int main() { memset(f,-1,sizeof(f)); cin >> n >> w >> b >> x; for (ll i = 1; i <= n; i++) { cin >> c[i]; sum += c[i]; } for (ll i = 1; i <= n; i++) cin >> cost[i]; for (ll i = 1; i <= n; i++) summ[i] = summ[i - 1] + c[i]; f[0][0] = w; for (ll i = 1; i <= n; i++) { for (ll j = 0; j <= summ[i]; j++) { for (ll k = 0; k <= c[i]; k++) { if (k > j) break; if (f[i - 1][j - k] >= 0) f[i][j] = max(f[i][j],min(f[i - 1][j - k] + x,w + (j - k) * b) - cost[i] * k); } } } for (ll i = sum; i >= 0; i--) { if (f[n][i] >= 0) { ans = i; break; } } cout << ans << endl; return 0; }

 , where
, where 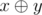 denotes the
denotes the 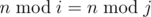 , where
, where 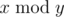 is the remainder of division
is the remainder of division 
 浙公网安备 33010602011771号
浙公网安备 33010602011771号