bzoj2693 jzptab

2693: jzptab

Time Limit: 10 Sec  Memory Limit: 512 MB
Submit: 1702  Solved: 667
[Submit][Status][Discuss]

Description

Input

一个正整数T表示数据组数

接下来T行 每行两个正整数 表示N、M

Output

T行 每行一个整数 表示第i组数据的结果

Sample Input

1
4 5

Sample Output

122
HINT
T <= 10000
N, M<=10000000

HINT

Source

版权所有者： 倪泽堃

分析：同bzoj2154,只是有多组数据，需要对算法进行优化.答案式子为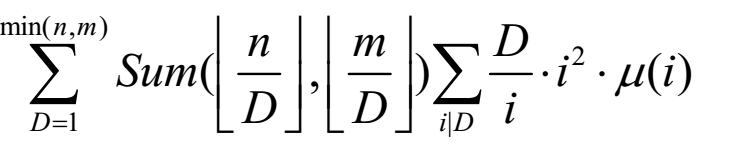，想要在根号复杂度内计算这个式子需要满足有分式，并且能够处理前缀和，唯一的问题就是计算前缀和了.

       如果还是按照每个数往它的倍数上累计答案来处理前缀和的话，复杂度差不多是O(nlogn)的，会T掉，一个比较好的做法是在线性筛的同时处理前缀和.考虑怎么处理,显然要处理的这一部分是一个积性函数，可以在线性筛的时候处理出来,在线性筛的时候，如果i和prime[j]互素，那么f[i*prime[j]] = f[i] * f[prime[j]].如果i % prime[j] == 0,那么prime[j]就是i的最小表示法中最小的质因子了.prime[j]*i相对于i多出来的因子都含有平方因子，μ值为0，对答案没有贡献.剩下的那一堆因子，因为i乘上了prime[j],F(i)中的D也应该乘上prime[j],所以F(i * prime[j]) = F(i) * prime[j].

       线性筛求积性函数值差不多都是分两种情况，一种是不互素直接相乘，另外一种大部分都是乘积的形式，打个表找找规律也可以.

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;

const ll maxn = 10000000, mod = 100000009;

ll prime[1000010], tot, sum[maxn + 10], g[maxn + 10], T, n, m;
bool vis[maxn + 10];

void init()
{
    g[1] = 1;
    for (ll i = 2; i <= maxn; i++)
    {
        if (!vis[i])
        {
            prime[++tot] = i;
            g[i] = (i - i * i) % mod;
        }
        for (ll j = 1; j <= tot; j++)
        {
            ll t = prime[j] * i;
            if (t > maxn)
                break;
            vis[t] = 1;
            if (i % prime[j] == 0)
            {
                g[t] = (g[i] * prime[j]) % mod;
                break;
            }
            g[t] = (g[i] * g[prime[j]]) % mod;
        }
    }
    for (ll i = 1; i <= maxn; i++)
        sum[i] = (sum[i - 1] + g[i]) % mod;
}

ll Sum(ll x, ll y)
{
    x %= mod;
    y %= mod;
    ll temp1 = (x * (x + 1) >> 1) % mod;
    ll temp2 = (y * (y + 1) >> 1) % mod;
    return temp1 * temp2 % mod;
}

int main()
{
    init();
    scanf("%lld", &T);
    while (T--)
    {
        scanf("%lld%lld", &n, &m);
        ll last = 0, ans = 0;
        if (n > m)
            swap(n, m);
        for (ll i = 1; i <= n; i = last + 1)
        {
            last = min(n / (n / i), m / (m / i));
            ans += (Sum(n / i, m / i) * (sum[last] - sum[i - 1] + mod) % mod) % mod;
            ans %= mod;
        }
        printf("%lld\n", (ans + mod) % mod);
    }

    return 0;
}