数学一本通第一章总结
这一章节讲的主要内容是数论方面的知识，设计到的知识点有:
1.整除
2.同余
3.最大公约数
3.1辗转相除法
3.2二进制算法
3.3最小公倍数
3.4扩展欧几里得算法
3.5求解线性同余方程
4.逆元
5.中国剩余定理
6.斐波那契数
7.卡特兰数
8.素数
8.1素数的判定
8.2素数的相关定理
8.3Miller-Rabin素数测试
8.4欧拉定理
8.5Pollard Rho算法求大数因子
9.BSGS及扩展算法
10.欧拉函数的线性筛法
其中Pollard Rho算法没有能够掌握,斐波那契数列通项公式的推导不是很熟，其它的知识点都已了解，历时：7天.
一、整除
关于整除，可以理解为一个数是另一个数的倍数，核心都围绕在这个倍数上，如果已知a|b,那么一般都可以假设b=ak,然后进行推导.如果不能整除，往往会有一个余数r,假设b%a=r,那么b = ak+r,当遇到余数的时候，通过余数展开式进行推导也是一种比较常用的方法.
例1：
2277: [Poi2011]Strongbox
Time Limit: 60 Sec Memory Limit: 32 MBSubmit: 498 Solved: 218
[Submit][Status][Discuss]
Description
Byteasar is a famous safe-cracker, who renounced his criminal activity and got into testing and certifying anti-burglary devices. He has just received a new kind of strongbox for tests: a combinatorial safe. A combinatorial safe is something different from a combination safe, even though it is opened with a rotary dial. The dial can be set in different positions, numbered from 0 to n-1. Setting the dial in some of these positions opens the safe, while in others it does not. And here is the combinatorial property, from which the name comes from: if x and y are opening positions, then so is (x+y) mod n too; note that is holds for x=y as well.
Byteasar tried k different positions of the dial: m1,m2….mk. The positions M1,M 2….Mk-1 did not open the safe, only the last position Mk did. Byteasar is already tired from checking these K positions and has thus absolutely no intention of trying the remaining ones. He would like to know however, based on what he already knows about the positions he tried, what is the maximum possible number of positions that open the safe. Help him by writing an appropriate program!
有一个密码箱，0到n-1中的某些整数是它的密码。
且满足，如果a和b都是它的密码，那么(a+b)%n也是它的密码(a,b可以相等)
某人试了k次密码，前k-1次都失败了，最后一次成功了。
问：该密码箱最多有多少不同的密码。
Input
The first line of the standard input gives two integers N and k, separated by a single space, (1<=K<=250000,k<=N<=10^14), The second line holds K different integers, also separated by single spaces, m1,m2….mk, 0<=Mi<N. You can assume that the input data correspond to a certain combinatorial safe that complies with the description above.
In tests worth approximately 70% of the points it holds that k<=1000. In some of those tests, worth approximately 20% of the points, the following conditions hold in addition: N< 10 ^8 and K<=100.
第一行n，k
下面一行k个整数，表示每次试的密码
保证存在合法解
1<=k<=250000 k<=n<=10^14
Output
Your program should print out to the first and only line of the standard output a single integer: the maximum number of the dial's positions that can open the safe.
一行，表示结果
Sample Input
42 5
28 31 10 38 24
28 31 10 38 24
Sample Output
14
分析：比较难的一道数学题.有两个结论：1.如果x是密码，那么gcd(x,n)也是密码. 2.如果x,y是密码，那么gcd(x,y)也是密码.根据这两个结论就能很轻松地解决本题了.
先来证明第一个结论：构造二元一次不定方程x*k - n*c = gcd(x,n),这个方程是一定有解的，也就是说一定存在一个 k使得x*k%n = gcd(x,n).而x是密码，(x+x)%n也是密码，所以k*x%n也是密码，那么gcd(x,n)就是密码.x就是题目中告诉的a[k].
再来证明第二个结论：gcd(x,y) = a*x + b*y,a,b有可能小于0.根据结论一可以推出
(p*x + q*y)%n是密码(p,q ≥ 0). 由a*x + b*y ≡ gcd(x,y)(mod n),变形一下可以得到:
a*x + b*y ≡ a*x + b*y + p*n*x + q*n*y(mod n) --> (a + p*n) * x + (b + q*n) * y ≡ gcd(x,y)(mod n).根据假设，((a + p*n) * x + (b + q*n) * y) % n是密码(x,y系数大于0)，那么gcd(x,y)也是密码.
把所有密码写出来以后，可以发现是一个x,2x,3x......的形式，所以任务就是找到一个最小的x使得x整除gcd(a[k],n).同时这个x不能整除a[j](1 ≤ j ＜ k).那么x就是gcd(a[k],n)的因子，根号的时间处理出来然后进行判断.判断的话也有一个优化，如果y是密码，gcd(x,y)不是密码，那么x也不是密码，所以在判断的时候看一下所有的gcd(a[j],n)是否被当前的因子整除就行了.
#include <cstdio> #include <cmath> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; ll n,k,a[250010],ans = n,cnt; bool check(ll x) { for (int i = 1; i <= cnt; i++) if (a[i] % x == 0) return false; return true; } ll gcd(ll a,ll b) { if (!b) return a; return gcd(b,a % b); } int main() { scanf("%lld%lld",&n,&k); for (int i = 1; i <= k; i++) { scanf("%lld",&a[i]); a[i] = gcd(a[i],n); } sort(a + 1,a + k); for (int i = 1; i < k; i++) if (a[i] != a[i - 1]) a[++cnt] = a[i]; for (ll i = 1; i <= sqrt(a[k]); i++) if (a[k] % i == 0) { if (check(i)) { ans = n / i; break; } else if (check(a[k] / i)) ans = n / a[k] * i; } printf("%lld\n",ans); return 0; }
总结：拿到一道题，一定要清楚地知道自己是要求解什么.对于这道题，如果没有两个结论，根本不知道自己要编程求啥.还要学会从结论来构造式子，比如我猜测gcd(a,n)是密码，那么我就要构造一个方程使得结果正好是让gcd(a,n)是密码，我能用什么知识解决这道题，我还需要什么信息，我就构造，得到这些信息.最后就是同余式中的变形，模数在同余式中是可以任意加减的，可以通过这个对式子进行适当变形.同样的，如果一个式子出现了多个变量，那么我也可以通过把其中一个变量当作模数来变得只剩下一个变量，一个比较直观的例子是中国剩余定理非互质版的推导.
二、同余
同余一般是在题目给定了模数下才会用到，但是有一些特殊情况比如数太大存不下，只考虑它在同余下的意义也是可以的.比较经典的例子就是：noip2014解方程.同余的运算基本上和四则运算差不多，只不过没有定义除法！涉及到除法就必须要用到逆元！比较常用的性质就是同幂性：a ≡ b (mod p) ---> a^n ≡ b^n (mod p).还有同乘性.
幂数取模问题：若幂次不大，则直接快速幂运算即可.若幂次很大，则用欧拉定理降幂,经典例题1：传送门，经典例题2：传送门
三、最大公约数
例2：欧几里得的游戏
题目描述
欧几里德的两个后代Stan和Ollie正在玩一种数字游戏，这个游戏是他们的祖先欧几里德发明的。给定两个正整数M和N，从Stan开始，从其中较大的一个数，减去较小的数的正整数倍，当然，得到的数不能小于0。然后是Ollie，对刚才得到的数，和M，N中较小的那个数，再进行同样的操作……直到一个人得到了0，他就取得了胜利。下面是他们用(25，7)两个数游戏的过程：
Start：25 7
Stan：11 7
Ollie：4 7
Stan：4 3
Ollie：1 3
Stan：1 0
Stan赢得了游戏的胜利。
现在，假设他们完美地操作，谁会取得胜利呢？
输入输出格式
输入格式：
第一行为测试数据的组数C。下面有C行，每行为一组数据，包含两个正整数M, N。（M, N不超过长整型。）
输出格式：
对每组输入数据输出一行，如果Stan胜利，则输出“Stan wins”；否则输出“Ollie wins”
输入输出样例
输出样例#1：
Submit: 712 Solved: 416
[Submit][Status][Discuss]
Submit: 3353 Solved: 2168
[Submit][Status][Discuss]
Submit: 4699 Solved: 1782
[Submit][Status][Discuss]
Submit: 313 Solved: 181
[Submit][Status][Discuss]
Stan wins Ollie wins
分析：可以用sg函数给秒掉，不过分析一下还是能发现规律的.设当前较大的数为m,较小的数为n,如果m/n==1,那么只能进行一种操作，如果m/n>1,那么我可以拿(m/n - 1) * n个，下一次对手就只能拿n个，进入到下一状态，我也可以全部拿完，让对手进入下一状态，也就是说如果我先到m/n>1的状态，那么我就掌控的局势，那么不断地辗转相除，更新答案即可.
#include <cstdio> #include <cmath> #include <cstring> #include <iostream> #include <algorithm> using namespace std; int c,f = 1; long long a,b; int main() { scanf("%d",&c); while (c--) { f = 1; scanf("%lld%lld",&a,&b); if (a < b) swap(a,b); while(b && a / b == 1 && a % b) { f = -f; long long t = a % b; a = b; b = t; } if (f == 1) puts("Stan wins"); else puts("Ollie wins"); } return 0; }
例3：
1477: 青蛙的约会
Time Limit: 2 Sec Memory Limit: 64 MBSubmit: 712 Solved: 416
[Submit][Status][Discuss]
Description
两只青蛙在网上相识了，它们聊得很开心，于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上，于是它们约定各自朝西跳，直到碰面为止。可是它们出发之前忘记了一件很重要的事情，既没有问清楚对方的特征，也没有约定见面的具体位置。不过青蛙们都是很乐观的，它们觉得只要一直朝着某个方向跳下去，总能碰到对方的。但是除非这两只青蛙在同一时间跳到同一点上，不然是永远都不可能碰面的。为了帮助这两只乐观的青蛙，你被要求写一个程序来判断这两只青蛙是否能够碰面，会在什么时候碰面。 我们把这两只青蛙分别叫做青蛙A和青蛙B，并且规定纬度线上东经0度处为原点，由东往西为正方向，单位长度1米，这样我们就得到了一条首尾相接的数轴。设青蛙A的出发点坐标是x，青蛙B的出发点坐标是y。青蛙A一次能跳m米，青蛙B一次能跳n米，两只青蛙跳一次所花费的时间相同。纬度线总长L米。现在要你求出它们跳了几次以后才会碰面。
Input
输入只包括一行5个整数x，y，m，n，L，其中x≠y < 2000000000，0 < m、n < 2000000000，0 < L < 2100000000。
Output
输出碰面所需要的跳跃次数，如果永远不可能碰面则输出一行"Impossible"
Sample Input
1 2 3 4 5
Sample Output
4
分析：可以用扩展欧几里得算法解决形如ax+by=gcd(a,b)的问题，但是本题要求解形如ax+by=c,而c不一定等于gcd(a,b)的问题，我们可以化简为(m-n)x + Ly = y-x。
解法肯定是通过解ax+by=d d=gcd(a,b)来得到题目所给方程的解，设l=m-n,p = L,c=y-x,化简为lx+py=c,第一个方程两边同时乘c/d,就得到第二个方程，也就是说l=a*c/d,p=b*c/d，根据解系，可以得到任意解l' = l + k*p/gcd(l,p),p' = p - k*l/gcd(l,p)。
为了求出最小正整数解，先mod模数再加上模数后mod模数，因为如果得到的是正数，加上模数后再模没有任何影响，如果是负数，加上模数后变成正数就正好是最小正整数解。注意的是这个模数要取绝对值。
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; long long x, y, m, n, L, ansx, ansy; long long gcd(long long a, long long b) { return b == 0 ? a : gcd(b, a%b); } long long exgcd(long long a, long long b, long long &x, long long&y) { if (b == 0) { x = 1; y = 0; return a; } long long r = exgcd(b, a%b, x, y); long long t = x; x = y; y = t - a / b * y; return r; } int main() { scanf("%lld%lld%lld%lld%lld", &x, &y, &m, &n, &L); if (x == y) { printf("0"); return 0; } else { long long a = m - n, b = y - x; long long t = exgcd(a, L, ansx, ansy); if (b % t == 0) { ansx = ansx * b / t; int tt = abs(L / t); ansx = (ansx % tt + tt) % tt; printf("%d", ansx); } else printf("Impossible"); } return 0; }
四、逆元
主要是知道逆元是什么东西，干什么用的，怎么求，如何递推地求出很多逆元.如果x和模数p互素，那么可以直接利用费马小定理来求.只需要求出x^(p-2) mod p就可以了.如果不满足这个要求，就利用扩展欧几里得算法来求.效率上可能扩展欧几里得算法的常数要小，但是费马小定理好写一下.线性求逆元关键就是记住一个式子：q[i] = (p - p/i) * q[p % i] % p.
例4：
Sumdiv
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 23172 | Accepted: 5769 |
Description
Consider two natural numbers A and B. Let S be the sum of all natural divisors of A^B. Determine S modulo 9901 (the rest of the division of S by 9901).
Input
The only line contains the two natural numbers A and B, (0 <= A,B <= 50000000)separated by blanks.
Output
The only line of the output will contain S modulo 9901.
Sample Input
2 3
Sample Output
15
Hint
2^3 = 8.
The natural divisors of 8 are: 1,2,4,8. Their sum is 15.
15 modulo 9901 is 15 (that should be output).
The natural divisors of 8 are: 1,2,4,8. Their sum is 15.
15 modulo 9901 is 15 (that should be output).
Source
分析：这道题有点复杂，涉及到约数嘛，肯定是先要分解一下，将原数变成唯一分解定律的表达形式，a = p1^x1*p2^x2*...*pn^xn,a^b = p1^x1b*p2^x2b*...*pn^xnb,那么约数和怎么求呢？如果把a^b的所有约数用唯一分解定律的表达形式写出来，就会发现p1和p2,p3,...,pn的所有的乘积的组合形式乘了一次，因式分解一下，可以得到sum = (1 + p1 + p1^2 + ... + p1^x1b) * (1 + p2 + ...+p2^x2b)*......
括号里的式子是一个等比数列，我们可以套用公式来计算，涉及到取模，就要求逆元，不过这个地方有点小技巧，如果求-1的逆元，答案是-1,但是程序给的是1,也就是说我们最好是求正数的逆元，等比数列求和公式上下同取负号就好了.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #include <cmath> using namespace std; const int mod = 9901; long long cnt[100010],wh[100010],tot,ans = 1; int a,b; void exgcd(long long a,long long b,long long &x,long long &y) { if (!b) { x = 1; y = 0; return; } exgcd(b,a % b,x,y); long long t = x; x = y; y = t - (a / b) * y; return; } long long qpow(long long a,long long b) { long long ans = 1; while (b) { if (b & 1) ans = (ans * a) % mod; a = (a * a) % mod; b >>= 1; } return ans; } int main() { scanf("%d%d",&a,&b); for (int i = 2; i <= sqrt(a); i++) { if (a % i == 0) { wh[++tot] = i; while (a % i == 0) { a /= i; cnt[i]++; } } } if (a) { wh[++tot] = a; cnt[a]++; } for (int i = 1; i <= tot; i++) { long long x,y; exgcd(wh[i] - 1,mod,x,y); ans = (ans * (( qpow(wh[i],cnt[wh[i]] * b + 1) - 1)* x) % mod) % mod; } printf("%lld\n",ans); return 0; }
总结：遇到跟一个数因数有关的题第一想法就是唯一分解定律！
五、斐波那契数列
斐波那契数列有几个非常常用的题型:1.找规律，一般有关斐波那契数列的题的规律都和斐波那契数列有关.2.矩阵快速幂求某一项.3.利用循环节取模算.经典例题1：传送门，经典例题2：传送门，裸的斐波那契数列快速求第n项的话套用公式：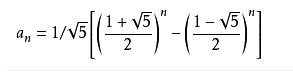
,如果n特别特别大的话，可以不管后面那一部分的.经典例题3：传送门
六、卡特兰数：传送门
七、Miller-Rabin素数测试
原理是利用费马小定理，不一定成立，一般选用2,3,5,7这4个数作为模数检验，如果费马小定理一直都成立，那么这个数几乎就是质数.
例5：
2190: [SDOI2008]仪仗队
Time Limit: 10 Sec Memory Limit: 259 MBSubmit: 3353 Solved: 2168
[Submit][Status][Discuss]
Description
作为体育委员，C君负责这次运动会仪仗队的训练。仪仗队是由学生组成的N * N的方阵，为了保证队伍在行进中整齐划一，C君会跟在仪仗队的左后方，根据其视线所及的学生人数来判断队伍是否整齐(如下图)。 
现在，C君希望你告诉他队伍整齐时能看到的学生人数。
Input
共一个数N。
Output
共一个数，即C君应看到的学生人数。
Sample Input
4
Sample Output
9
HINT
【数据规模和约定】 对于 100% 的数据，1 ≤ N ≤ 40000
分析：如果以C君所在的点为原点来建立坐标系，那么只有x,y互素才能被看到，否则就会被(x / gcd(x,y),y / gcd(x,y))挡住，计算互素的数的对数的经典做法就是利用欧拉函数，记录1~i与i互素的点的个数然后*2就好了，在这道题里我们求出∑φ(i) (2 <= i < n) ,答案*2+3就好了（还有0,1 1，0 1 1这三个点）.
#include <cmath> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; int n,ans,phi[40010]; void getphi() { phi[1] = 1; for (int i = 2; i <= n; i++) if (!phi[i]) for (int j = i; j <= n; j+=i) { if (!phi[j]) phi[j] = j; phi[j] = phi[j] / i * (i - 1); } } int main() { scanf("%d",&n); getphi(); for (int i = 2; i < n; i++) ans += phi[i]; printf("%d\n",ans * 2 + 3); return 0; }
八、BSGS及其扩展算法
这个算法是用来求解a ^ x = b(mod p)中的x的一个根号复杂度的算法.取m=sqrt(p),x = i*m - j.那么式子就变成了:
a^(i*m) = b*a^j (mod p).先枚举j,将右边式子的结果对应的j存到hash表中，再来枚举i,在hash表中查找对应结果的j.注意：如果a%p==0那么是无解的.
例6:
2242: [SDOI2011]计算器
Time Limit: 10 Sec Memory Limit: 512 MBSubmit: 4699 Solved: 1782
[Submit][Status][Discuss]
Description
你被要求设计一个计算器完成以下三项任务：
1、给定y,z,p,计算Y^Z Mod P 的值；
2、给定y,z,p，计算满足xy≡ Z ( mod P )的最小非负整数；
3、给定y,z,p，计算满足Y^x ≡ Z ( mod P)的最小非负整数。
Input
输入包含多组数据。
第一行包含两个正整数T,K分别表示数据组数和询问类型（对于一个测试点内的所有数据，询问类型相同）。
以下行每行包含三个正整数y,z,p，描述一个询问。
Output
对于每个询问，输出一行答案。对于询问类型2和3，如果不存在满足条件的，则输出“Orz, I cannot find x!”，注意逗号与“I”之间有一个空格。
Sample Input
【样例输入1】
3 1
2 1 3
2 2 3
2 3 3
【样例输入2】
3 2
2 1 3
2 2 3
2 3 3
【数据规模和约定】
对于100%的数据，1<=y,z,p<=10^9，为质数，1<=T<=10。
3 1
2 1 3
2 2 3
2 3 3
【样例输入2】
3 2
2 1 3
2 2 3
2 3 3
【数据规模和约定】
对于100%的数据，1<=y,z,p<=10^9，为质数，1<=T<=10。
Sample Output
【样例输出1】
2
1
2
【样例输出2】
2
1
0
2
1
2
【样例输出2】
2
1
0
HINT
Source
分析：几个算法的大合集.对于第一组询问，快速幂就好了.对于第二组询问，相当于解一个同余方程，用扩展欧几里得算法搞一搞就好了.对于第三组询问，用BGSG来做，关于BGSG算法的详细讲解，可以参看：传送门.
#include <cstdio> #include <cmath> #include <map> #include <cstring> #include <iostream> #include <algorithm> using namespace std; int T, K; typedef long long ll; ll y, z, p, x, block; map <ll, ll> m; ll qpow(ll a, ll b, ll mod) { ll res = 1; while (b) { if (b & 1) res = (res * a) % mod; a = (a * a) % mod; b >>= 1; } return res; } void solve1() { scanf("%lld%lld%lld", &y, &z, &p); printf("%lld\n", qpow(y, z, p)); } ll exgcd(ll a, ll b, ll &x, ll &y) { if (!b) { x = 1; y = 0; return a; } ll temp = exgcd(b, a % b, x, y); ll t = x; x = y; y = t - (a / b) * y; return temp; } void solve2() { scanf("%lld%lld%lld", &y, &z, &p); ll tx, ty, td; td = exgcd(y, p, tx, ty); if (z % td != 0) puts("Orz, I cannot find x!"); else { tx = tx * (z / td) % p; ll mmod = p / td; tx = (tx % mmod + mmod) % mmod; printf("%lld\n", tx); } } void solve3() { scanf("%lld%lld%lld", &y, &z, &p); m.clear(); if (y % p == 0) { puts("Orz, I cannot find x!"); return; } else { block = ceil(sqrt(p)); ll ans; for (int i = 0; i <= block; i++) { if (i == 0) { ans = z % p; m[ans] = i; continue; } ans = (ans * y) % p; m[ans] = i; } ll t = qpow(y, block, p); ans = 1; for (int i = 1; i <= block; i++) { ans = (ans * t) % p; if (m[ans]) { ll t = i * block - m[ans]; printf("%lld\n", (t % p + p) % p); return; } } } puts("Orz, I cannot find x!"); } int main() { scanf("%d%d", &T, &K); while (T--) { if (K == 1) solve1(); if (K == 2) solve2(); if (K == 3) solve3(); } return 0; }
当p不是质数的时候，就要用到扩展BSGS算法了.思想就是不断地提gcd出来，直到互质，然后套用普通的BSGS算法.
例7：
1467: Pku3243 clever Y
Time Limit: 4 Sec Memory Limit: 64 MBSubmit: 313 Solved: 181
[Submit][Status][Discuss]
Description
小Y发现，数学中有一个很有趣的式子： X^Y mod Z = K 给出X、Y、Z，我们都知道如何很快的计算K。但是如果给出X、Z、K，你是否知道如何快速的计算Y呢？
Input
本题由多组数据（不超过20组），每组测试数据包含一行三个整数X、Z、K（0 <= X, Z, K <= 10^9）。 输入文件一行由三个空格隔开的0结尾。
Output
对于每组数据：如果无解则输出一行No Solution，否则输出一行一个整数Y(0 <= Y < Z)，使得其满足XY mod Z = K，如果有多个解输出最小的一个Y。
Sample Input
5 58 33
2 4 3
0 0 0
2 4 3
0 0 0
Sample Output
9
No Solution
No Solution
HINT
Source
分析：扩展BSGS.对于P与A不互质的情况，我们就不断地提gcd出来，直到互质.然后换元套用普通的bsgs算法即可.具体的解法：
--来自Clove_unique的博客.事实上只需要根据式子
就可以用普通的BSGS算法了，求出x-k后，加上k就是x.
一个思想：从普通算法向扩展算法的延伸，如果由互质版本变成不互质版本，想办法变成互质版本，可以取gcd.一定要是等价变形.在变形的时候要判断无解的情况.
#include <cstdio> #include <cmath> #include <map> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; ll a, b, p, block; map <ll, ll> m; ll gcd(ll a, ll b) { if (!b) return a; return gcd(b, a % b); } ll qpow(ll a, ll b) { ll res = 1; while (b) { if (b & 1) res = (res * a) % p; a = (a * a) % p; b >>= 1; } return res; } ll exbsgs(ll a, ll b, ll p) { if (b == 1) return 0; ll temp = gcd(a, p), cnt = 0, t = 1; while (temp != 1) { if (b % temp != 0) return -1; cnt++; b /= temp; p /= temp; t = t * (a / temp) % p; temp = gcd(a, p); } m.clear(); block = sqrt(p); ll res = b, ta = qpow(a, block); for (ll i = 1; i <= block; i++) { res = res * a % p; m[res] = i; } for (ll i = 1; i <= block; i++) { t = t * ta % p; if (m[t]) return i * block - m[t] + cnt; } return -1; } int main() { while (scanf("%lld%lld%lld", &a, &p, &b) && a && b && p) { ll ans = exbsgs(a % p, b % p, p); if (ans != -1) printf("%lld\n", ans); else puts("No Solution"); } return 0; }
中国剩余定理和BSGS的互质版本与非互质版本的转换都是依靠不断提取gcd,来变成互质的版本.
九、欧拉函数的线性筛法
因为欧拉函数是积性函数，所以可以在线性筛素数的同时把欧拉函数给求出来：
void shai() { for (int i = 2; i <= maxn; i++) { if (!vis[i]) { prime[++tot] = i; phi[i] = i - 1; } for (int j = 1; j <= tot; j++) { int t = i * prime[j]; if (t > maxn) break; vis[t] = 1; if (i % prime[j] == 0) { phi[t] = pht[i] * prime[j]; break; } phi[t] = phi[i] * (prime[j] - 1); } } }
习题2：传送门
习题3：传送门
习题4：传送门
其它资料：传送门
