noip模拟赛 伪神
题目背景
一切就绪
但愿,这样就好
自那之后的五年——
作为封印持续增大的结果,在我体内积蓄了庞大的光精灵的力量
在幻灯结界里觉醒过来的我,和从封印解放出的德米奥格,就如同字面意思所述的,获得了等同于神的力量
德米奥格的眼睛能通过他人的认知,洞悉过去——
我窥视者它们
之后,我醒悟到了一切事实
我应做的时期只此无二
将这份等同于神一般的特意能力,赌上性命以及一切,救回毁灭中的世界,为了挽救我的伙伴们——
吸收了本在驱君体内的劫之眼后,德米奥格真正获得了万能的力量
世界被重新创造,一切都将被再构造
那是德米奥格在创造世界——是侵犯着神之领域的行为
作为后果,如今我在这里
处在这个她们看不到,而我可以看到他们的位置
如今,我就在,过去曾被人们认为神灵所在的领域
那里,不存在任何人
那便是,这份永远的孤独——
哎???
我感到,有一只温暖的手,在我背后轻轻的拍了一下……
这个只有我存在的世界——到底是谁……?

当它轻盈地出现时——附在身上的万能的感觉消失了
【这样一来,你就只是普通的人类】
哎? 【你已经变回了,无力,只有一个人是无法继续生活下去的女孩子了】
我慌张地转过头去,在那里,是我的分身,德米奥格

德米奥格……吗?
【我就是我——没有名字——你和我应该是同样的存在】
【刚才的瞬间,我以自己的力量,夺取你的力量】
【以你的力量而具现化出的我,本部应该存在心灵】
【但是——】
【在你的心中,生出了另一颗心】
【并非作为菊理,我德米奥格,只此一次,想实现自己的愿望】
那是?
【菊理,作为一个人类抓住自己的幸福——】
【那是,观察着你们的战斗后,我德米奥格的愿望……】
【等同于神的我,将会永远守护着你们……】
【活下去吧——】
题目描述
是……!
我回答的瞬间——
眼前,德米奥格的身影消失了
德米奥格……我,会努力的活下去的……
请你一直守护我哦~

Lass给你出了一道倒闭题:
给你一个n个点的树还有一只青蛙。
由于这棵树被夺去了生命,所以你需要通过青蛙来复活上面的节点,有m次操作。
每次操作有三个参数a,b,t
然后会给你a条链,青蛙都会把每条链上面的所有点增加一秒
然后会给你b个点,青蛙都会把每个点子树里面的所有点增加一秒
注意青蛙是大公无私的,所以每次牠不会管这个节点之前有没有增加过,都会增加一秒
但是因为树失去了生命太多了,所以只有被增加了>=t秒的节点会重获新生(t可以为0)
而且因为你的黑框眼镜是假的,所以每次的操作是独立的
也就是说,每次操作增加的秒数,在这次操作结束的瞬间就会被青蛙回收,这棵树的所有节点又会失去生命
多么残酷的一道题啊
输入输出格式
输入格式:
第一行二个数n,m
之后n-1行每行两个数x,y表示x和y直接连有边
之后m次操作
每次操作先是一行三个数a,b,t,意义已上述
之后a行每行两个数x,y表示青蛙从x跳到y,每个节点增加了1s
之后b行每行一个数x表示青蛙把x的子树里面每个节点增加了1s
输出格式:
m行,第i行一个数表示第i次操作有多少个节点获得了新生
输入输出样例
5 2 1 2 2 3 3 4 4 5 1 1 2 2 3 3 1 2 2 1 3 2 5
1 3
5 2 1 2 2 3 2 4 3 5 2 3 3 2 3 3 3 3 3 3 4 2 3 1 4 2 3 4 5 1 2 4 3
2 3
说明
样例#3,#4,#5,#6,#7见下发的文件
【由乃暖心的小提示】
这个题最大读入量有约24MB
经实测
由于luogu的评测姬非常快,所以这个题里面
用getchar的读入优化和fread的差距不到200ms
所以我这次不提供fread模版了
如果有兴趣使用可以粘上场比赛发的那个
然后std用时800ms,大家可以根据这个估算时间
注意到了真正的NOIP出题人肯定不会这么良心的
所以不可能告诉你读入量多少,std用时多少这种事情,需要自己去判断的
【子任务】
子任务会给出部分测试数据的特点。
如果你在解决题目中遇到了困难, 可以尝试只解决一部分测试数据。
每个测试点的数据规模及特点如下表:
| 测试点 | n | m | a的和 | b的和 | t | 特殊性质 |
|---|---|---|---|---|---|---|
| 1 | 100 | 10 | 50 | 50 | <=1 | 数据随机 |
| 2 | 100 | 10 | 50 | 50 | <=1 | 数据随机 |
| 3 | 100 | 10 | 50 | 50 | 无限制 | 数据随机 |
| 4 | 100 | 10 | 50 | 50 | 无限制 | 无 |
| 5 | 1000 | 200 | 600 | 400 | <=1 | 链 |
| 6 | 2000 | 5000 | 500000 | 500000 | 无限制 | 链 |
| 7 | 5000 | 5000 | 500000 | 500000 | 无限制 | 无 |
| 8 | 5000 | 5000 | 500000 | 500000 | 无限制 | 无 |
| 9 | 5000 | 5000 | 500000 | 500000 | 无限制 | 无 |
| 10 | 100000 | 20000 | 49784 | 50216 | 无限制 | 链 |
| 11 | 100000 | 20000 | 50306 | 49694 | 无限制 | 无 |
| 12 | 100000 | 25000 | 200000 | 0 | 无限制 | 无 |
| 13 | 100000 | 60000 | 300000 | 300000 | 无限制 | 无 |
| 14 | 100000 | 80000 | 0 | 400000 | 无限制 | 链 |
| 15 | 100000 | 80000 | 0 | 400000 | <=1 | 数据随机 |
| 16 | 100000 | 80000 | 400000 | 400000 | 无限制 | 数据随机 |
| 17 | 100000 | 8000 | 400000 | 0 | 无限制 | 无 |
| 18 | 100000 | 10000 | 0 | 1000000 | 无限制 | 无 |
| 19 | 100000 | 100000 | 500000 | 500000 | 无限制 | 无 |
| 20 | 100000 | 100000 | 1000000 | 1000000 | 无限制 | 链 |
| 21 | 100000 | 100000 | 1000000 | 1000000 | 无限制 | 链 |
| 22 | 100000 | 100000 | 1000000 | 1000000 | 无限制 | 链 |
| 23 | 100000 | 100000 | 1500000 | 1000000 | 无限制 | 无 |
| 24 | 100000 | 200000 | 1500000 | 400000 | 无限制 | 无 |
| 25 | 100000 | 400000 | 1500000 | 1000000 | 无限制 | 无 |
对于100%的数据,n <= 100000 , m <= 400000 , a的和 <= 1500000 , b的和 <= 1000000
【说明】
【样例1说明】
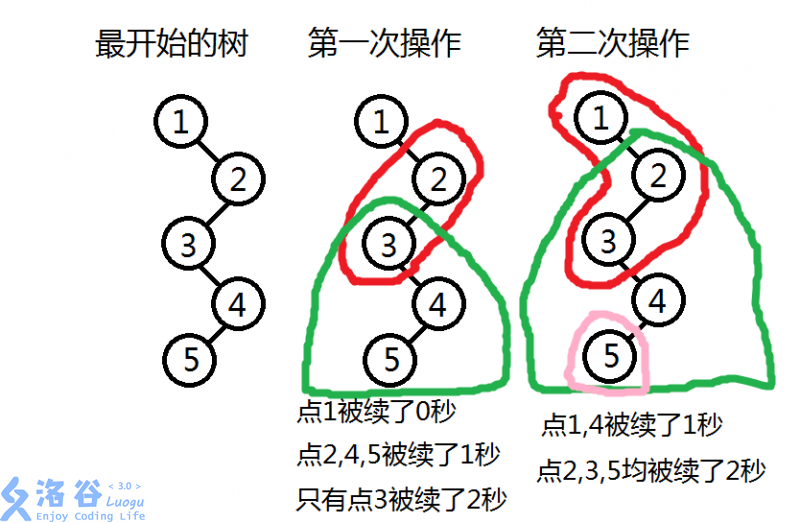
【样例2说明】
饶了我吧,图我是画不出来了GG
第一次操作:
点1,4被增加了0秒,点2被增加了1秒,点5被增加了3秒,点3被增加了5秒,有两个点被增加了不小于3秒,所以答案为2
第二次操作:
点1被增加了2秒,点2被增加了4秒,点3被增加了3秒,点4被增加了3秒,点5被增加了1秒,有三个点被增加了不小于3秒,所以答案为3.
分析:每次对一个子树进行操作,可以想到dfs序,又每次对一条链操作,可以想到树链剖分,将树转化为区间,每次进行区间+操作,可以想到差分/线段树,事实上线段树非常麻烦,因为要查询>=t的个数,所以不如用差分.那么基本思路就出来了:dfs序+树链剖分+差分.
差分在修改的时候比较快,但是查询就必须要扫一遍,比较费时间,而且查询操作又比较多,能不能优化呢?因为一开始所有的数都是相同的,每次修改一个区间实际上只是修改了两个端点的值,每一次修改操作最多会使2个点的值与其它点不同。有很多点其实数值是一样的,我们可以把一样的一些点给变成一段,如果查询到一个点>=t,那么答案加上这一段的长度就可以了.因为段是连续的,所以在查询之前把所有的操作的点从小到大排序.
一个优化:如果每次都memset差分数组,由于数组很大,会T掉,如何避免memset呢?可以用时间戳或者对赋值过的点修改,显然这道题用后一种方法.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int maxn = 100010; int n, m, head[maxn], to[maxn * 2], nextt[maxn * 2], tot = 1, cnt, top[maxn], sum[maxn * 100]; int son[maxn], sizee[maxn], fa[maxn], pos[maxn], mx[maxn], dep[maxn], q[maxn * 100], tt, ans, cnt2; int read() { int f = 1, res = 0; char c = getchar(); while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); } while (c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); } res *= f; return res; } void update(int x, int y) { q[++cnt2] = x; q[++cnt2] = y + 1; sum[x]++; sum[y + 1]--; } void add(int x, int y) { to[tot] = y; nextt[tot] = head[x]; head[x] = tot++; } void dfs(int u) { sizee[u] = 1; for (int i = head[u]; i; i = nextt[i]) { int v = to[i]; if (v == fa[u]) continue; fa[v] = u; dep[v] = dep[u] + 1; dfs(v); if (sizee[v] > sizee[son[u]]) son[u] = v; sizee[u] += sizee[v]; } } void dfs2(int u, int tp) { pos[u] = mx[u] = ++cnt; top[u] = tp; if (son[u]) { dfs2(son[u], tp); mx[u] = max(mx[u], mx[son[u]]); } for (int i = head[u]; i; i = nextt[i]) { int v = to[i]; if (v != son[u] && v != fa[u]) { dfs2(v, v); mx[u] = max(mx[u], mx[v]); } } } void jump(int x, int y) { int u = top[x], v = top[y]; while (u != v) { if (dep[u] < dep[v]) { swap(u, v); swap(x, y); } update(pos[u], pos[x]); x = fa[u]; u = top[x]; } if (dep[x] < dep[y]) swap(x, y); update(pos[y], pos[x]); } int main() { n = read(), m = read(); for (int i = 1; i < n; i++) { int x, y; x = read(); y = read(); add(x, y); add(y, x); } dfs(1); dfs2(1, 1); while (m--) { int a, b, t; cnt2 = 0; a = read(); b = read(); t = read(); for (int i = 1; i <= a; i++) { int x, y; x = read(); y = read(); jump(x, y); } for (int i = 1; i <= b; i++) { int x; x = read(); update(pos[x], mx[x]); } q[++cnt2] = n + 1, q[++cnt2] = 1; sort(q + 1, q + 1 + cnt2); cnt2 = unique(q + 1, q + 1 + cnt2) - q - 1; tt = 0, ans = 0; for (int i = 1; i < cnt2; i++) { tt += sum[q[i]]; if (tt >= t) ans += q[i + 1] - q[i]; } for (int i = 1; i <= cnt2; i++) sum[q[i]] = 0; printf("%d\n", ans); } return 0; }




