noip模拟赛 Massacre at Béziers

题目背景

下发压缩包链接: https://pan.baidu.com/s/1geC4ooz 密码: 3vpt

所有的一切———所有的一切都被染成了红与黑。

翻卷的红莲烈焰舔舐着大地，释放出异抽的黑烟突破天际，红色的死亡与黑色的阴霾正将所有的一切掩埋殆尽……

对于这个世界来说就根本不存在什么救赎。

我向天空仰望。

东方的天空已经开始拉下夜的帷幕。

正将街道烧尽的烈焰与黑烟和接踵而至的炫目夕阳光芒混杂在一起——就像是脏腑一样的天空的颜色。

我祈祷着——

如果这火焰是主对我们的审判，要将一切都烧尽的话，

就让这和永远的烈焰同化的世界不断的燃烧，直到回归为尘土吧。

给予像我们这样可悲的罪人以祝福。

给予在灵魂的牢笼里沉睡的所有怠惰的人们以祝福。

———赐予祝福吧———

隐秘的神啊——

就是现在，请赐予恩宠给您无知迷茫的子民们吧。

阿门。

他们告诫世人，这个世界将永远不会走到尽头

因为最终审判已经降下

并且不会更改，而在那地狱中，

永恒的业火与罪罚不在他处，就在此世间。

（想了解这个直接搜题目名即可）

题目描述

我妻蛤乃给你出了一道送命题：

黄梅时节家家雨，青草池塘处处蛙~

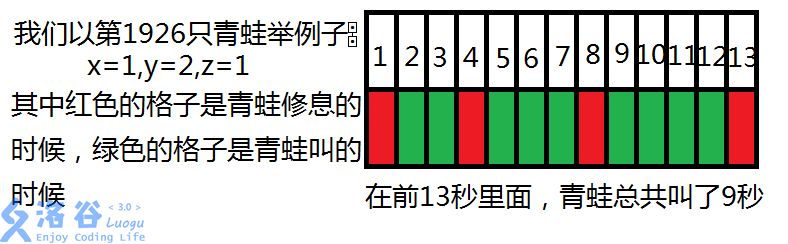
有n只青蛙，第i只青蛙会每过xi秒会连续叫yi秒。然而由于青蛙的寿命在增加，所以从第二次开始每次休息结束后这只青蛙连续叫的时间会增加zi秒。

给定n只青蛙，每一只的xi，yi，zi，以及时间t，求在前t秒中，所有青蛙共叫了多少秒。

输入输出格式

输入格式：

 

第一行两个数n和t

之后n行，第i+1行每行三个非负整数xi,yi,zi

 

输出格式：

 

一行一个数表示答案

 

输入输出样例

输入样例#1：

8 10
9 1 1
1 9 9
4 1 0
2 3 3
1 0 0
1 4 0
9 2 5
1 2 1

输出样例#1：

34

输入样例#2：

1 233333
233 233 233

输出样例#2：

223081

输入样例#3：

10 100000000
1 0 0
1 0 5
1 2 2
1 2 8
1 3 0
1 5 0
1 5 2
1 5 5
1 7 0
1 8 3

输出样例#3：

845787522

说明

样例#4，#5见下发的文件

【子任务】

子任务会给出部分测试数据的特点。 如果你在解决题目中遇到了困难, 可以尝试只解决一部分测试数据。

每个测试点的数据规模及特点如下表:

测试点编号	n的范围	t的范围	特殊性质
测试点1	n = 1
测试点2	n = 100	t <= 100	x = 0
测试点3	n = 100	y = 0
测试点4	n = 100	z = 0
测试点5	n = 100
测试点6	n = 100000	t <= 100	x = y = z
测试点7	n = 100000	t <= 100	z = 0
测试点8	n = 100000	y = 0
测试点9	n = 100000	t <= 100000
测试点10	n = 100000

对于100%的数据，n <= 100000 , t <= 2000000000，x + y + z > 0

0 <= x , y , z <= 2000000000

【说明】

【样例1说明】

每只青蛙分别叫了1,9,2,6,0,8,1,7秒

【样例2说明】

那只青蛙叫了223081秒

【样例3说明】

每只青蛙分别叫了0,99993675,99990000,99994999,75000000,83333333,99990002,99993676,87500000,99991837秒

分析：这道题思路还是挺好想的，利用等差数列前n项和公式S=na0 + n*(n-1)*d/2.二分找一下使得S <= t的最大n,那么这n段时间是可以直接处理的，剩下的边界特判一下就可以了.

      比较毒瘤的是二分的时候会爆long long,我在处理的时候特判了一下是否<=2000000000.

#include <cstdio>
#include <cmath>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;
ll n, t, ans, res;
ll x, y, z;

void solve()
{
    scanf("%lld%lld%lld", &x, &y, &z);
    ll l = 1, r = 2000000000, ans = 0;
    while (l <= r)
    {
        ll mid = (l + r) >> 1;
        if (2000000000 / mid >= (mid - 1) * z / 2 && (1ll * (x + y) * mid + 1ll * (mid - 1) * mid / 2 * z) <= t)
        {
            l = mid + 1;
            ans = mid;
        }
        else
            r = mid - 1;
    }
    ll temp = (1ll * (x + y) * ans + 1ll * (ans - 1) * ans / 2 * z);
    ll tt = 0;
    tt += temp - 1ll*ans * x;
    if (x < t - temp)
        tt += t - temp - x;
    res += tt;
}

int main()
{
    scanf("%lld%lld", &n, &t);
    while (n--)
    solve();
    printf("%lld\n", res);

    return 0;
}