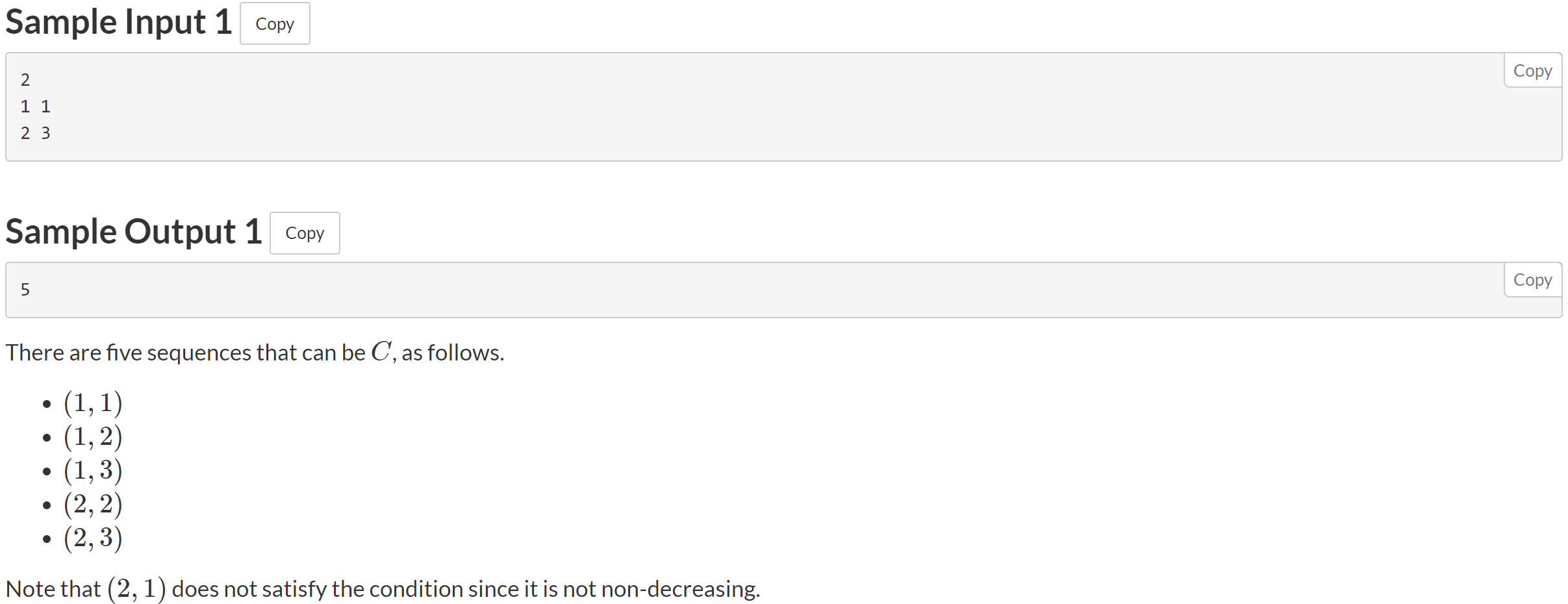
题意
![]()

题解
公理1:此题支持O(N2)。
公理2:对于每个合法序列,其值单调不减。
灵感1(公理1):是否可以DP?
性质1(公理2):在一个序列不断"递增"的过程中,其能够选择的最小值单调不降。
公理3:方案数具有累加性,不具有后效性。
答案1(灵感1、公理3):可以保存下所有状态,状态设计为dp[i][j],其中i为处理到第几个数字,j为当前能够接受的最小值,dp[i][j]为当前方案数。
性质2(公理2、公理3):对于每一个数字$i\left ( 1\leq i\leq n \right )$,当设置"能够选择的最小值"为$j$时,其方案数为:数字为i-1,且"能够选择的最小值"<=j的方案数的和。
答案2(性质2):$dp[i][j]=\sum_{0}^{j}dp[i-1][j]$
#include<cstdio> #include<iostream> #define int long long using namespace std; const int MAXN = 4000; const int MOD = 998244353; int a[MAXN], b[MAXN]; int dp[MAXN][MAXN]; int sum[MAXN][MAXN]; int max(int a, int b) { if (a > b)return a; else return b; } signed main() { int n; scanf("%lld", &n); for (int i = 1; i <= n; i++) scanf("%lld", &a[i]); for (int i = 1; i <= n; i++) scanf("%lld", &b[i]); for (int i = a[1]; i <= b[1]; i++) { dp[1][i] = 1; } sum[1][0] = dp[1][0]; for (int i = 1; i <= 3000; i++) { sum[1][i] = sum[1][i - 1] + dp[1][i]; sum[1][i] %= MOD; } for (int i = 2; i <= n; i++) { int l = a[i]; int r = b[i]; for (int j = l; j <= r; j++) { dp[i][j] = sum[i-1][j]; dp[i][j] %= MOD; } sum[i][0] = dp[i][0]; for (int j = 1; j <= 3000; j++) { sum[i][j] = sum[i][j - 1] + dp[i][j]; sum[i][j] %= MOD; } } int ans = 0; for (int i = 0; i <= 3000; i++) { ans = ans+dp[n][i]; ans %= MOD; } printf("%lld\n", ans); return 0; }


