题意
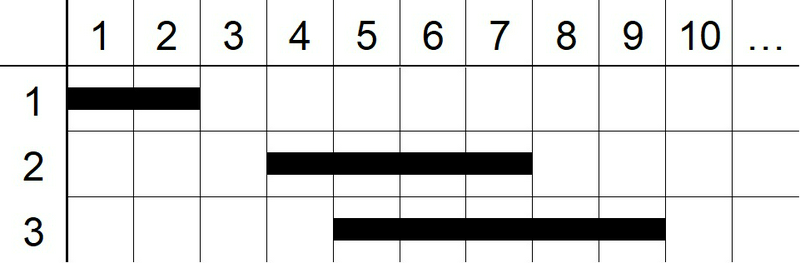
给定N堵墙,一拳超人每次选一个范围攻击,如果某个墙有任意一格在这个范围内,这堵墙就销毁了。
求:最小的挥拳数量

题解
条件1:要打掉所有墙。
条件2:挥拳数量要尽量小。
条件3:一次挥拳只能销毁一定范围内的墙。
性质1:在挥拳数量尽量小的情况下,所有墙必须被销毁。
性质2:如果两次挥拳能够合并成一次挥拳且满足性质1,就应当计数为1。
性质3:挥拳一定是有逻辑、有顺序的。
答案1:应当对所有墙以左端点为主键,右端点为次键排序。(条件3/性质3/性质1)
反证1:不能直接对每个墙的右端点进行攻击,因为一个大墙可以覆盖整个区间。
答案2:定义minR为一定范围内能够攻击的墙的右端点的最小值,那么[minR,minR+D-1]就是能够摧毁的墙的左端点的合法取值区间。(性质1/性质2)
复杂度:{O(n),O(n)}
#include<cstdio> #include<iostream> #include<algorithm> using namespace std; const int MAXN = 4e5; struct Wall { int l, r; bool operator <(const Wall &another)const { if (l == another.l)return r < another.r; return l < another.l; } }s[MAXN]; int main() { int n, D; scanf("%d%d", &n, &D); for (int i = 1; i <= n; i++) { scanf("%d%d", &s[i].l, &s[i].r); } sort(s + 1, s + n + 1); int cnt = 0; for (int i = 1; i <= n;i++) { int minR=s[i].r; cnt++; for (int j = i + 1;s[j].l<=minR+D-1&&j<=n; j++) { minR = min(minR, s[j].r); i = j; } } printf("%d\n", cnt); return 0; }


