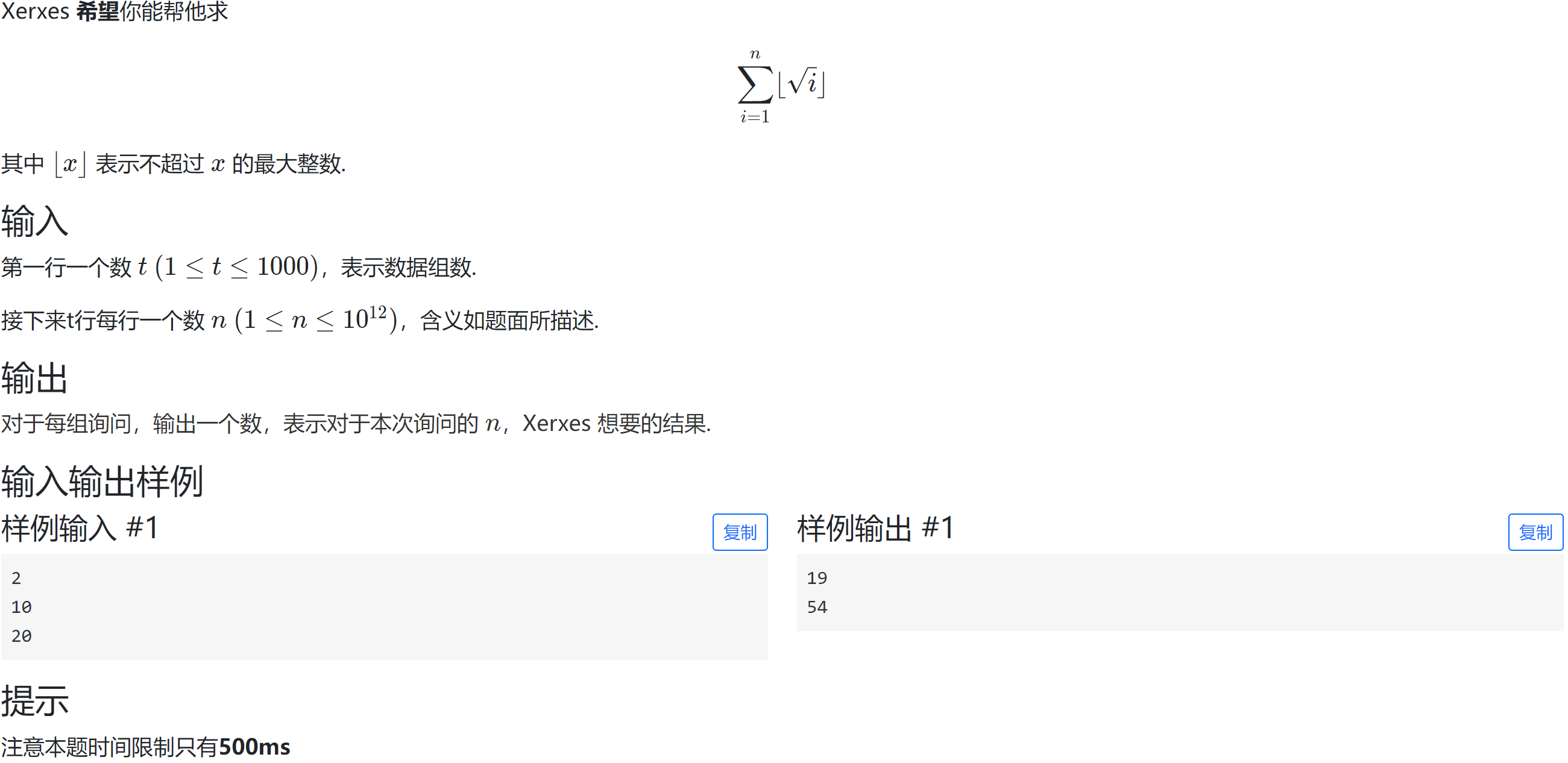
方法1
类比除法分块,打表1 -- 1e6,直接用sum解决。可解决n范围为1到1e12的数据。
#include<cstdio>
#include<iostream>
#include<cmath>
#define int long long
using namespace std;
const int MAXN=2e6;
int a[MAXN],sum[MAXN];
void init(){
a[1]=3;
for(int i=2;i<=1000000;i++){
a[i]=((i+1)*(i+1)-1-(i*i-1))*i;
}
for(int i=1;i<=1000000;i++){
sum[i]=sum[i-1]+a[i];
}
}
int solve(int n){
int tmp=sqrt(n);
int val1=sum[tmp-1];
int val2=(n-tmp*tmp+1)*tmp;
return val1+val2;
}
signed main(){
init();
int t;
scanf("%lld",&t);
while(t--){
int n;
scanf("%lld",&n);
printf("%lld\n",solve(n));
}
return 0;
}
方法2
从方法1了解到a[i]=((i+1)*(i+1)-1-(i*i-1))*i,而sum数组是a[i]的前缀和。那么,能否用数学方法优化这个式子呢?
答案是可以的。
![]()
#include<cstdio>
#include<iostream>
#include<cmath>
#define int long long
using namespace std;
int solve(int ttmp){
int n=sqrt(ttmp)-1;
int val1=n*(n+1)*(2*n+1)/3+n*(n+1)/2;
n=ttmp;
int tmp=sqrt(ttmp);
int val2=(n-tmp*tmp+1)*tmp;
return val1+val2;
}
signed main(){
int t;
scanf("%lld",&t);
while(t--){
int n;
scanf("%lld",&n);
printf("%lld\n",solve(n));
}
return 0;
}



