
写在"基石"之前
位运算有着相对独立性。因此,如果对某些数字进行运算,如果不考虑实际流程和组合,只考虑最终结果的和,可以考虑到:是否可以利用位运算"相对独立性"的性质?
思路1:从十进制到二进制
可以看到,最终要求得的结果其实就是一个序列所有子序列的异或和,但是考虑到位运算的相对独立性,应该可以注意到:所有子序列的异或和,其实就是每一位的异或和的许多种组合。(这个对于新人需要慢慢理解)最终,在位运算层面上拼凑出来的答案,就等于是所有"子序列的异或和"的宏观数字的值。
那么,重新考虑二进制数字的性质,不难发现,如果将一个十进制数字转化为二进制,那么有的地方是1,有的地方是0。
由于题目已经给了任意一段子段的 或和 ,那么将这些值都或起来,可以得到一个"奇妙的数字"。这个奇妙的数字实际上就是其中一种可行方案的 所有数字的 或和。
也就是说,如果这个奇妙的数字的某一位是0,那么压根没有数字这一位是1。换句话讲,这些0都具有美妙的"唯一性",也就是不管怎么样取"子序列",这些0都只有0可以"爱"。
从前面,我们讲到:二进制运算具有相对独立性,换句话讲,完全可以使用二进制的拼凑和排列组合公式来表示宏观"物体"(也就是十进制组合)的排列方式。
那么现在,需要求的就是:给定一个数字(<2^31),问有多少种可以异或出这个数字的方法。
思路2:二进制的循环计算
现在需要求的是:给定一个数字(<2^31),问有多少种可以异或出这个数字的方法。
那么对于这个数字进行分解,对于每一位,不难发现可以分成1和0两种情况。
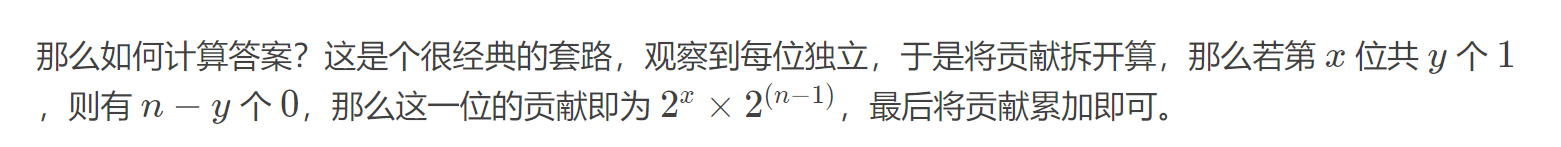
如果将所有2^x统计起来,可以发现其实就是所有给定答案的 或和。也就是说,答案是(ans|=x),(ans)*2^(n-1)。
#include<cstdio>
#include<iostream>
#define int long long
using namespace std;
const int MOD = 1e9 + 7;
int poww(int a, int b) {
int ans = 1;
while (b) {
if (b & 1)ans *= a;
a *= a;
a %= MOD;
ans %= MOD;
b >>= 1;
}
return ans;
}
signed main(){
int t;
scanf("%lld", &t);
while (t--){
int n, m;
scanf("%lld%lld", &n, &m);
int ans = 0;
for (int i = 1; i <= m; i++) {
int l, r, x;
scanf("%lld%lld%lld", &l, &r, &x);
ans |= x;
}
ans = ans * poww(2, n - 1);
printf("%lld\n", ans%MOD);
}
return 0;
}



