P2568 GCD（线性筛-欧拉函数 模板）

---

 有两个易错点：

1.欧拉函数的定义是1到n内互质的数，但是“互质”不一定要都是质数，其实就只需要gcd(a,b)=1就可以计算进去。所以，就不能放弃a=1,b=1的情况，

2.第一次做的时候自认为应该避免i=j的情况，但问题是经过化简之后的式子本身就已经考虑到i=j这个情况，并以此作为继续计算的基础。

其他想法：做题要做会。就算不会，也得认了。不要想着自己"AC"了就算是牛逼了，经验+1。（这样可以做到"喜"提打铁）

---

 

#include<cstdio>
#include<iostream>
#include<cstring>
#define ll long long
using namespace std;
const int MAXN=2e7;
int primes[MAXN],cnt=0;
bool isPrime[MAXN];
ll phi[MAXN],sumPhi[MAXN];


void init(int n){
	memset(isPrime,1,sizeof(isPrime));
	
	phi[1]=1;
	isPrime[1]=0,phi[2]=1;
	for(int i=2;i<=n;i++){
		if(isPrime[i])primes[++cnt]=i,phi[i]=i-1;
		for(int j=1;j<=cnt&&primes[j]*i<=n;j++){
			isPrime[i*primes[j]]=0;
			if(i%primes[j]==0){//能整除 
				phi[i*primes[j]]=primes[j]*phi[i];
				break;
			}else phi[i*primes[j]]=phi[i]*phi[primes[j]];
		}
	}
	
	for(int i=1;i<=n;i++)
		sumPhi[i]=sumPhi[i-1]+phi[i];
	
	return;
}


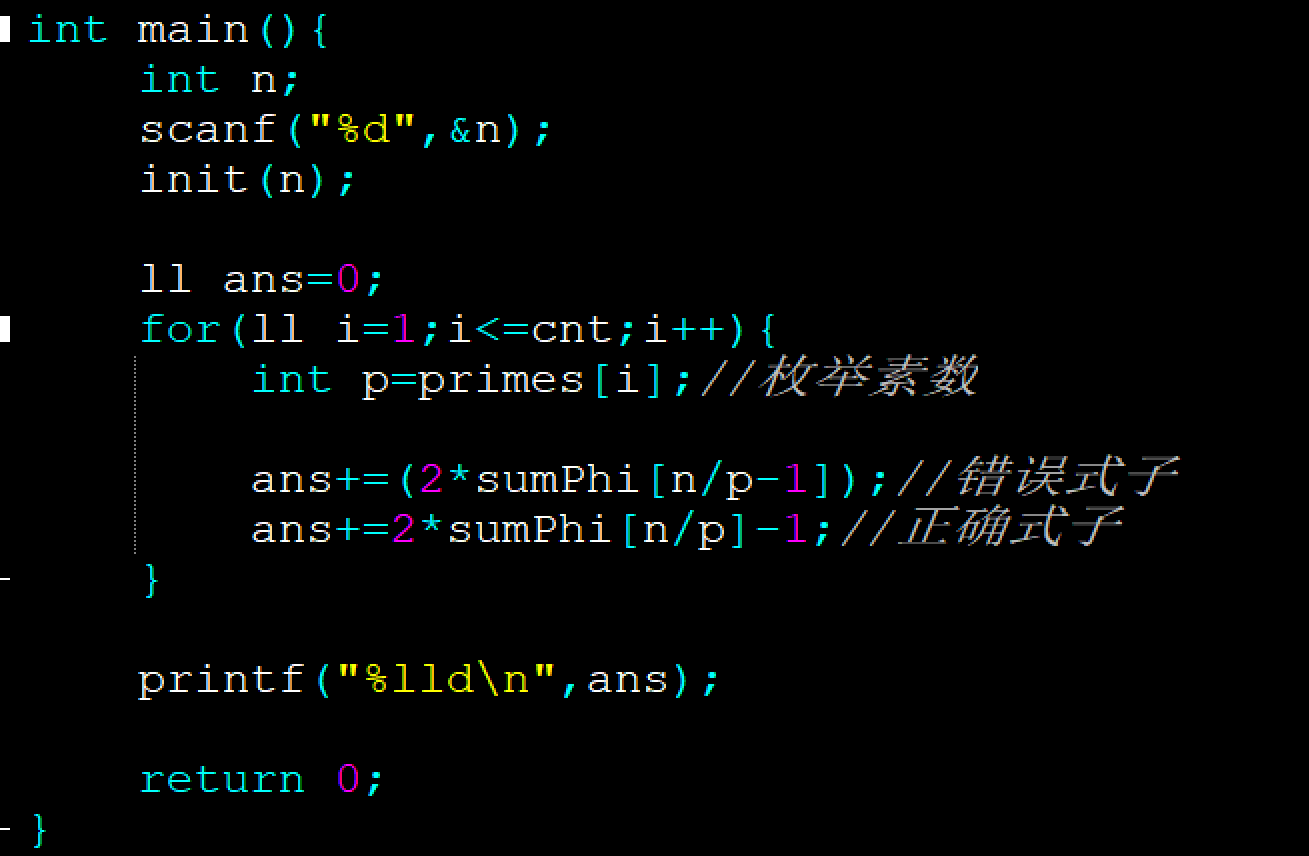
int main(){
	int n;
	scanf("%d",&n);
	init(n);
	
	ll ans=0;
	for(ll i=1;i<=cnt;i++){
		int p=primes[i];//枚举素数
		 
		ans+=(2*sumPhi[n/p-1]);//错误式子 
		ans+=2*sumPhi[n/p]-1;//正确式子 
	}
	
	printf("%lld\n",ans);
	
	return 0;
}