题目链接:https://atcoder.jp/contests/abc226
Round decimals
题意:给定浮点数 x ,输出 x 四舍五入后的结果
思路:round(val)
Counting Arrays
题意:给你 n 个长度为 li 的序列 ai ,判断有多少对 (i,j) 满足序列 ai 与 aj 不同,定义两个序列不同当且仅当存在一位不同。
思路:使用set<vector<int>>自动排除重复答案,直接输出size即可。
set的使用方法:
set<vector<int>> s; vector<int> arr; arr.push_back(a); s.insert(arr); cout<<s.size()<<endl;
#include <bits/stdc++.h>
using namespace std;
set<vector<int>> s;
int n, l, a;
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
vector<int> arr;
cin >> l;
for (int i = 0; i < l; i++) {
cin >> a;
arr.push_back(a);
}
s.insert(arr);
}
cout << s.size() << endl;
return 0;
}
Martial artist
题意:你需要学 n 种招式,第 i 种招式花费 ti 分钟,在学习第 i 个招式前必须学习 ki 个编号小于 i 的招式 ai,j ,问你最少需要多久可以学会第 n 个招式。
思路:一开始的想法是拓扑排序,但是实际上可能形成好几个子图,数据不保证只有一个图。
考虑反向拓扑排序。即直接从需要最后学会的招式开始BFS即可。
Teleportation
题意:在平面直角坐标系内给你 n 个点 Pi ,其中 1 ≤ i ≤ n ,定义一种操作 (a,b) 是把 P(x,y) 变成 P(x+a,y+b) ,你可以定义无数种形如 (a,b) 的操作,两种操作被认为是相同的当且仅当 a=a′ 且 b=b′ ,你希望对点 1 ≤ i ≤ n 进行无数次某一种操作,使其一定能变成另外 n−1 个点中的每一个,问至少定义多少种操作
思路:一开始想O(n^2)遍历所有情况,然后去重。但是实际上,题意要求的是可以重复使用同一个招式。那么,假设一个技能可以移动(1,1),那么直接向右上方走路可以无限使用这个技能,即可以一直使用。换句话讲,在遍历(a,b)和(c,d)的同时,要尝试s=gcd(a-c,b-d),然后答案(e,f)转化为(e/s,f/s)再进行去重。
Just one
题意:给你 n 点 m 边的无向图,问有多少种加边的方案,使得每个点的出度都是1?
错误:一开始读假题了,以为是要按方向走,每个点只能走一次,然后给定图能否走成功。
思路:出度为1联想拓扑排序,再增加一个联想和数学证明。
我们贪心的将最外面的边强制设为出向边,那么我们就要考虑内部有没有环。
如果有环,且不是简单环,明显不行。
如果没有环,整个图是个树或其他什么东西,明显也不可能出度都为1。
那么就可以联想到:最终给定的图只能转化为一个简单环加上一些枝叶。
归纳性质,容易发现:当且仅当m==n时,该条件成立。加上判环就可以保证答案的正确性了。
出度图可以反向图,也就是一个连通分量是2个答案贡献。
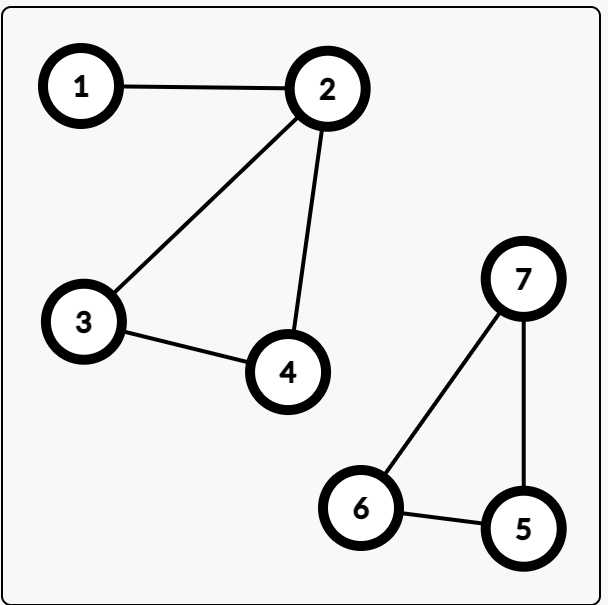 答案为4。
答案为4。



