Educational Codeforces Round 117 (Rated for Div. 2) B. Special Permutation

---

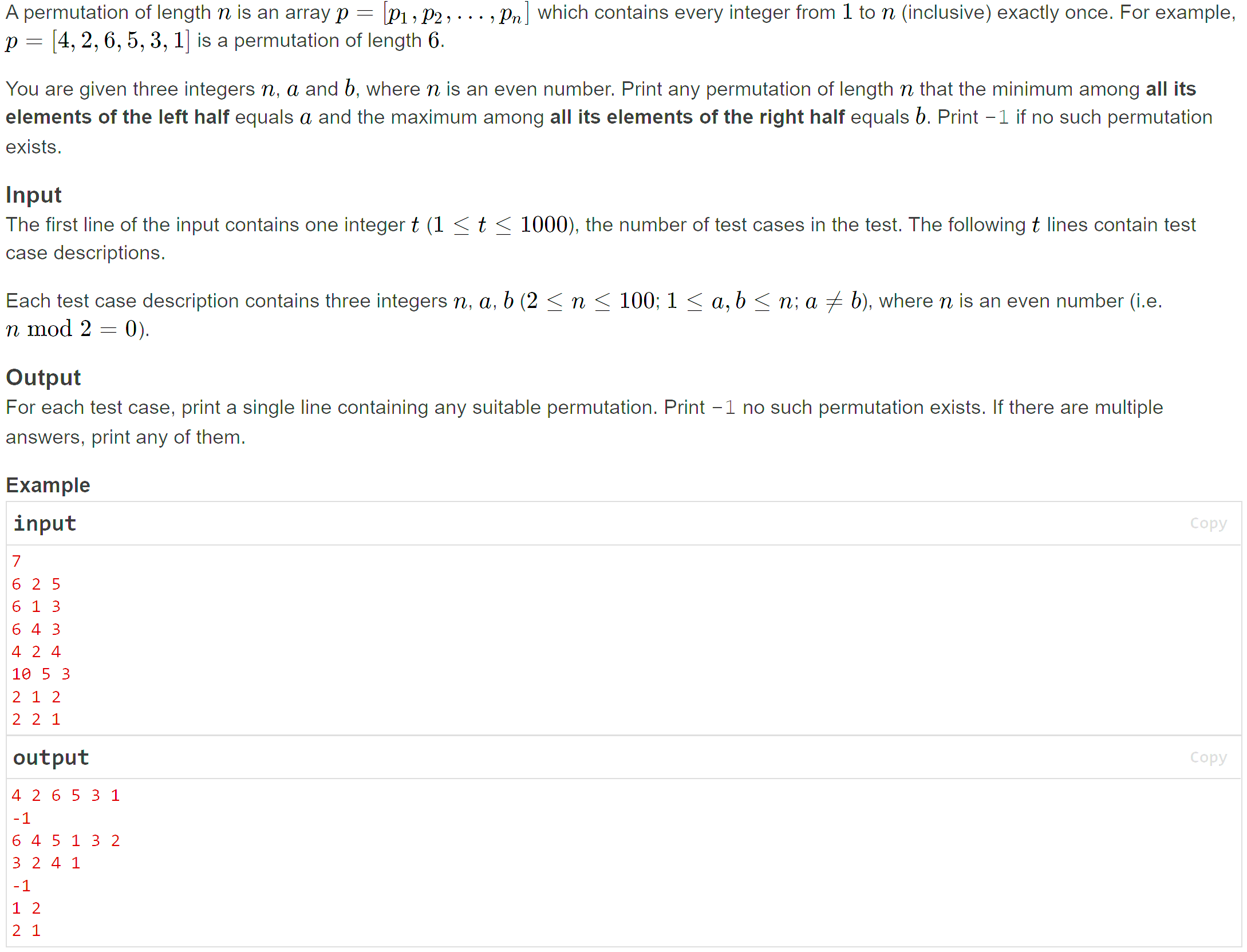
一开始想到了判断输出-1的充分条件为a、b与(n/2)之间的大小关系，但实际上没有考虑到abs(a-b)大小所带来的后效性影响。

换句话讲，除了贪心地把a，b分别放到最前面和最后面，还分别需要模拟填充和模拟判断，也就是"下苦功夫"。

在这种思路明显的题目中，我们常常要考虑：是否在代码的实现上会遇到困难？

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;

int val[200],index;

void solve(){
	int n,a,b;
	scanf("%d%d%d",&n,&a,&b);
	
	val[1]=a,val[n]=b;
	index=n;
	for(int i=2;i<=(n/2);i++){
		if(index!=a&&index!=b){
			val[i]=index;
		}else{
			i--;
		}
		index--;
	}
	for(int i=(n/2)+1;i<=n-1;i++){
		if(index!=a&&index!=b){
			val[i]=index;
		}else{
			i--;
		}
		index--;
	}
	
	int minn=n,maxx=1;
	for(int i=1;i<=(n/2);i++)
		minn=min(minn,val[i]);
	for(int i=(n/2)+1;i<=n;i++)
		maxx=max(maxx,val[i]);
	if(minn!=a||maxx!=b){
		printf("-1\n");
		return;
	}
	
	for(int i=1;i<=n;i++)
		printf("%d ",val[i]);
	printf("\n");
}

int main(){
	int t;
	scanf("%d",&t);
	while(t--){
		solve();
	}
	return 0;
}