
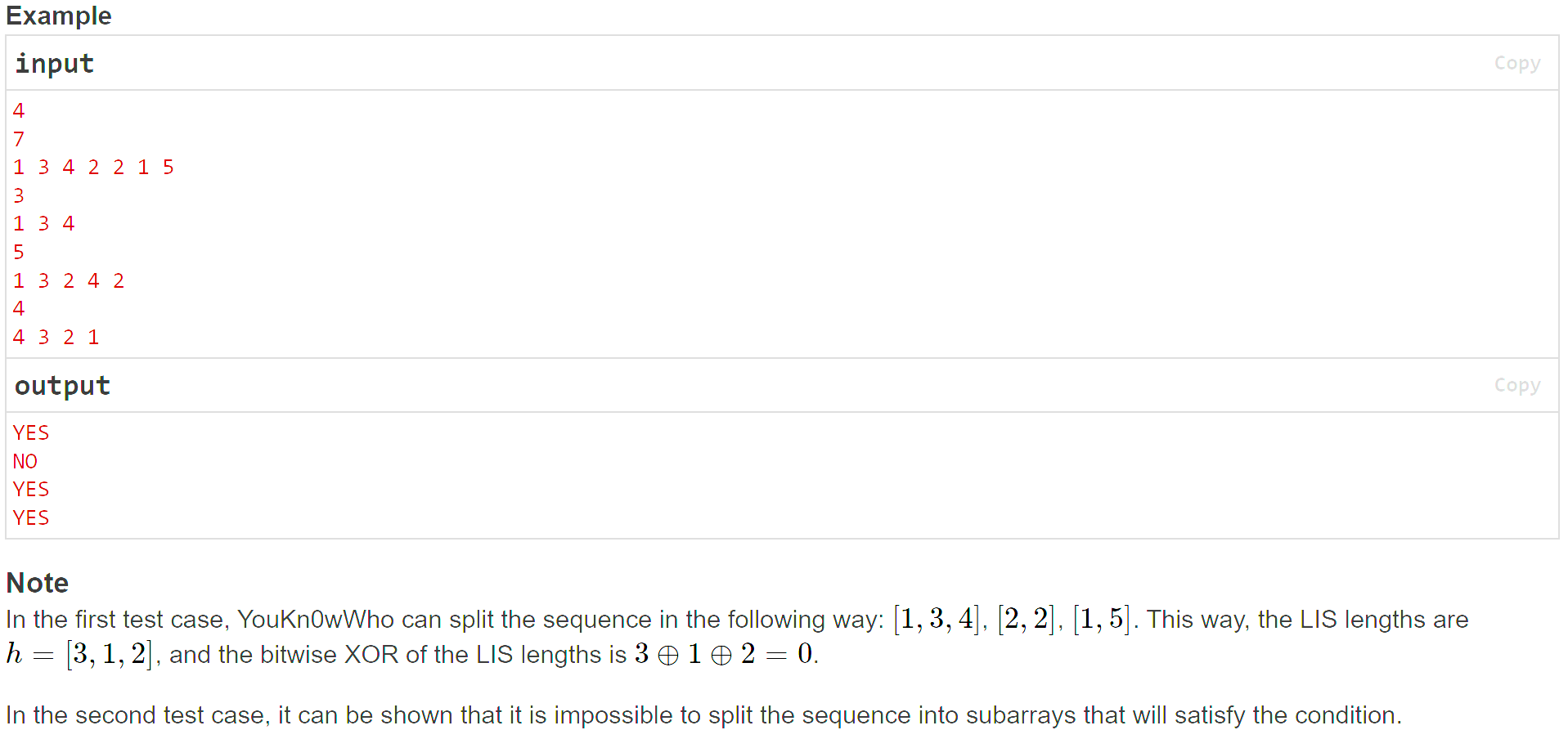
一开始怎么都想不到思路。实际上,不能从LIS和DP的角度考虑,而是要从题目要求的东西的性质入手,再结合LIS在当前题目下的特殊性质,才能找到一个比较好的解法。
题目中,分割的每个序列的"值"都是LIS的长度,考虑一种极限情况:分成n个序列。在这种情况下,如果n为偶数,就得到了一个正确的结果("YES")。
接下来,问题就转化为了:如何将奇数下的情况转化为偶数的特殊情况?显然,一个奇数y=2*n+1,那么我们就考虑,能否单独拿出来一个数字,这个数字的值为1,再用两个或其他偶数个数字对它进行异或,从而得到答案("YES" or "NO")?
场上并没有想到偶数个数字什么时候可以"值"为1,这是因为下意识地将答案联系到了LIS的性质上,而没有将LIS的性质对于该题目的要求进行数学上的抽象。
其实很容易发现,如果两个相邻数字中,前面的数字大于等于后面的那个数字,这两个数字就可以用来对1进行异或,就得到了答案。
#include<cstdio> #include<iostream> using namespace std; const int MAXN=2e5; int a[MAXN]; int main(){ int t; scanf("%d",&t);; while(t--){ int n; scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d",&a[i]); } if(n%2==0){ printf("YES\n"); continue; } bool flag=0; for(int i=1;i<=n-1;i++){ if(a[i]>=a[i+1]){ flag=1; } } if(flag) printf("YES\n"); else printf("NO\n"); } return 0; }



