一、整体流程
做了A和B。
大胆猜想,直接写码……
二、具体题目
A. Windblume Ode

(1)读题
①场上:从样例解释中发现,输出时的顺序无关紧要,换句话讲,输出1 2 3 ... 8 9与输出6 9 1 2 3 ... 8都算正确。
题目要求集合大小尽量大,但不需要总值最大。同时,需要判断合数或者素数。
那么,如果保证是合数的话,就可以直接输出;如果是素数的话,可以想办法减为合数。
②改进:可以大胆猜想算法。一般对于最简单的一道题,都有着非常容易写出的代码,即不考察算法和码力,转而考虑数学猜想和证明能力。对于此题,大胆猜想可随意删除一个数字,如果保证删除此数后新的和为合数,就贪心的输出答案。
③证明:在和本身为合数的情况下,直接输出答案。如果本身不是合数,那么和一定是质数,也一定是奇数。既然和是奇数,那么只要再减去一个奇数就可以变成偶数了,既然是偶数,那么也必然是合数。考虑到和为奇数,那么一定有起码一个奇数,即充分性。
(2)做题
由于int sum=0;定义在了函数外,wa了两次。
素数筛

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> using namespace std; bool isGood[300000];//�Ƿ�Ϊ���� void init(){ for(int i=2;i<=20000;i++){ for(int j=2;j<=20000;j++){ if(i*j>20000)continue; else isGood[i*j]=1; } } } int a[200]; int main() { //cout<<Miller_Rabin(3)<<endl; init(); int T; scanf("%d",&T); while(T--){ int n; scanf("%d",&n); int sum=0; for(int i=1;i<=n;i++){ scanf("%d",&a[i]); sum+=a[i]; } //printf("isGood[%d]=%d\n",sum,isGood[sum]); if(isGood[sum]){//�����Ǻ��� printf("%d\n",n); for(int i=1;i<=n;i++){ printf("%d ",i); } printf("\n"); }else{//�����Ǻ��� //ȥ��һ������ʹ��ȥ�����sumΪ������Ȼ������� int removeIndex=0; for(int i=1;i<=n;i++){ if(isGood[sum-a[i]]){ removeIndex=i; //printf("removeIndex:%d\n",removeIndex); break; } } printf("%d\n",n-1); for(int i=1;i<=n;i++){ if(i!=removeIndex){ printf("%d ",i); } } printf("\n"); } } return 0; }
Miller-Rabin

#include<cstdio> #include<cstring> #include<algorithm> using namespace std; int prime[10]={2,3,5,7,11,13,17,19,23,29}; int Quick_Multiply(int a,int b,int c) { long long ans=0,res=a; while(b) { if(b&1) ans=(ans+res)%c; res=(res+res)%c; b>>=1; } return (int)ans; } int Quick_Power(int a,int b,int c) { int ans=1,res=a; while(b) { if(b&1) ans=Quick_Multiply(ans,res,c); res=Quick_Multiply(res,res,c); b>>=1; } return ans; } bool Miller_Rabin(int x) { int i,j,k; int s=0,t=x-1; if(x==2) return true; if(x<2||!(x&1)) return false; while(!(t&1)) { s++; t>>=1; } for(i=0;i<10&&prime[i]<x;++i) { int a=prime[i]; int b=Quick_Power(a,t,x); for(j=1;j<=s;++j) { k=Quick_Multiply(b,b,x); if(k==1&&b!=1&&b!=x-1) return false; b=k; } if(b!=1) return false; } return true; } int a[200]; int main() { int T; scanf("%d",&T); while(T--){ int sum=0; int n; scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d",&a[i]); sum+=a[i]; } if(!Miller_Rabin(sum)){//?????????? printf("%d\n",n); for(int i=1;i<=n;i++){ printf("%d ",i); } printf("\n"); }else{ //???????????????????sum??????????????? int removeIndex=0; for(int i=1;i<=n;i++){ if(!Miller_Rabin(sum-a[i])){ removeIndex=i; //printf("removeIndex:%d\n",removeIndex); break; } } printf("%d\n",n-1); for(int i=1;i<=n;i++){ if(i!=removeIndex){ printf("%d ",i); } } printf("\n"); } } return 0; }
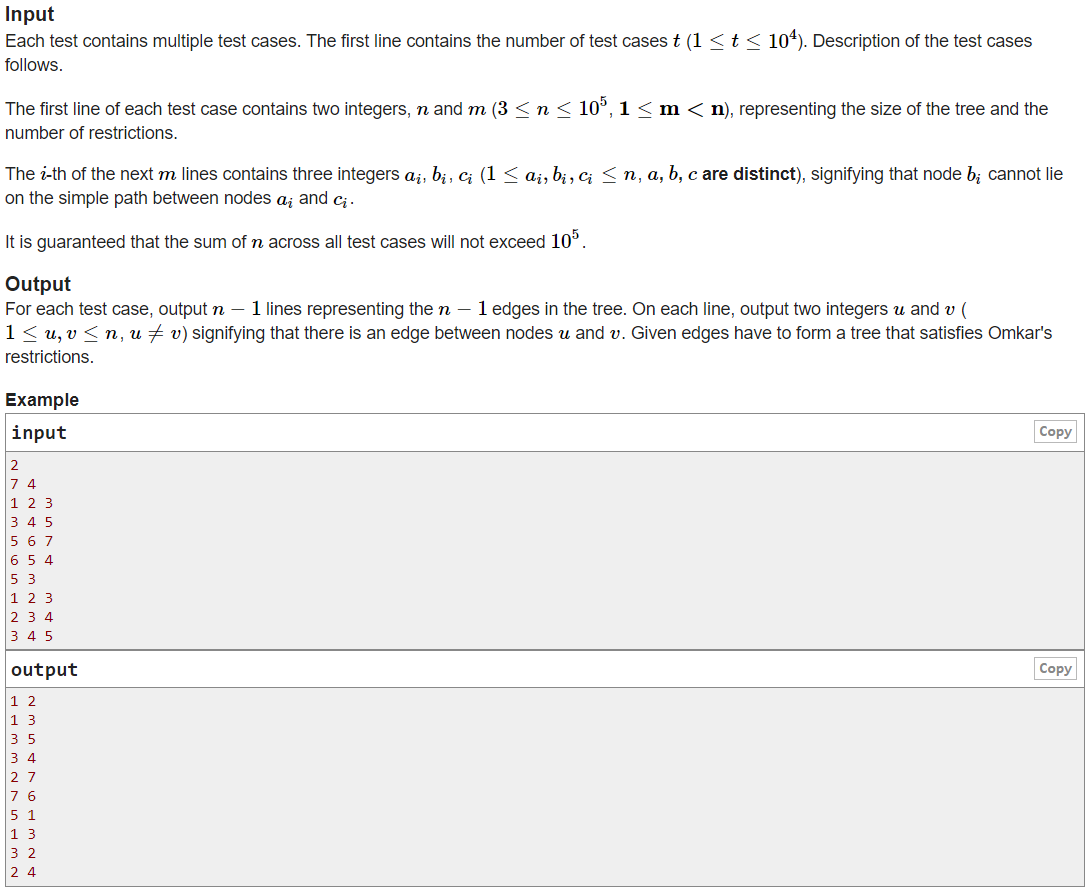
B. Omkar and Heavenly Tree
(1)读题
①场上:题意要求两点之间的简单路径中不能有违法点,考虑重新建图。注意到两点之间如果有任何限制,那么连接这两个点,就可以直接忽略掉这些限制。但是如果直接连接输出答案的话,可能出现环或者其他构造答案,因此要换一种连点越过限制的方法。
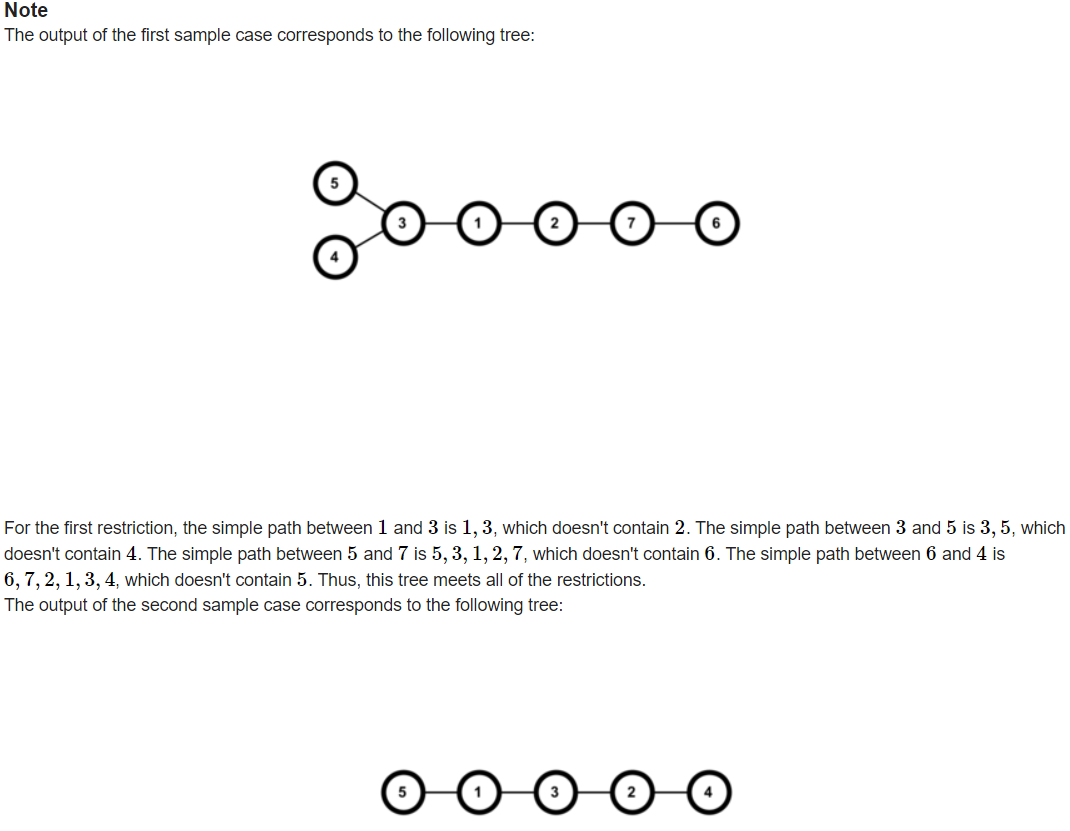
②改进:div2的B题一般不会太难,难度主要在思维上。重新审视要求,发现对于树的类型和形状没有确切的规定,输出答案十分自由。那么联想到"菊花图"

③证明:菊花图有着一个特性:任意两点之间的中间点必然有且只有中心点和两点上面的点。联合a,b,c均独特的特性,得到正解为构造一颗深度为2的菊花图.
(2)做题

#include<cstdio> #include<iostream> using namespace std; bool baned[200000]; int main(){ int t; scanf("%d",&t); while(t--){ int n,m; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++)baned[i]=0; for(int i=1;i<=m;i++){ int a,b,c; scanf("%d%d%d",&a,&b,&c); baned[b]=1; } for(int i=1;i<=n;i++){ if(!baned[i]){//根 for(int j=1;j<=n;j++){ if(j!=i) printf("%d %d\n",i,j); } break; } } } return 0; }