一、整体流程
晚了一小时参赛,被第一道题卡了许久,下一道题卡常卡了许久后火速做完了另外两道暴力
二、具体题目
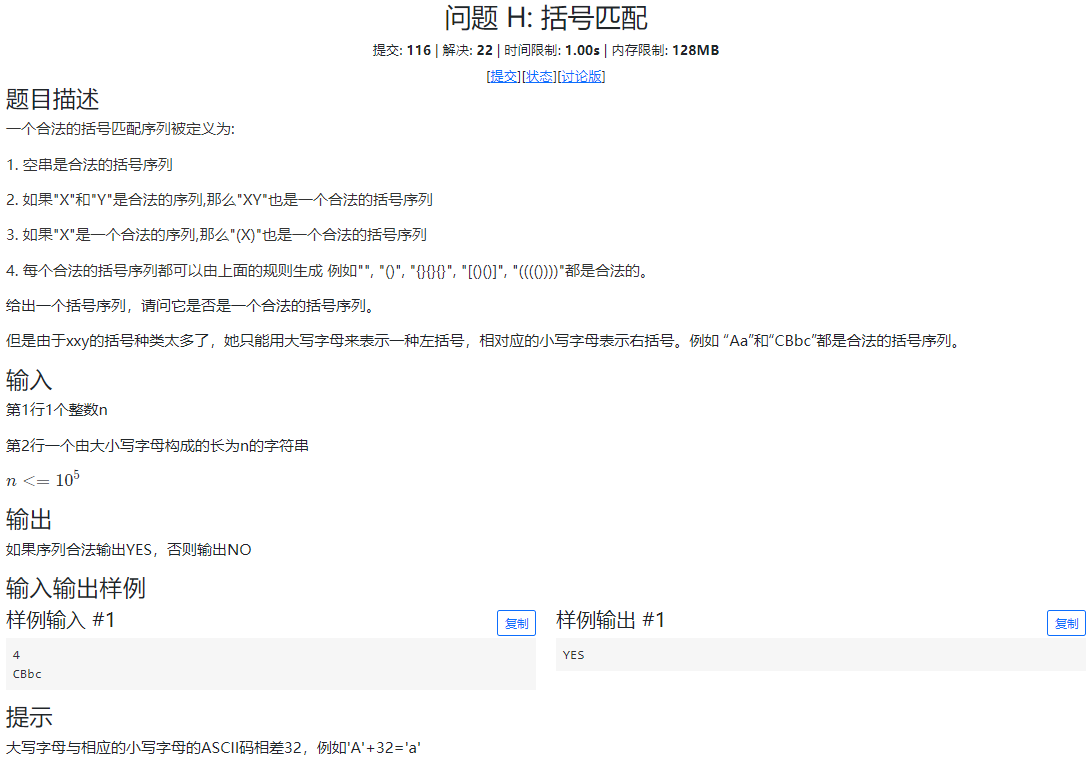
1.问题 H:括号匹配
(1)读题
①场上:场上考虑到用栈,放进去左括号后遇到右括号出栈,如果不是需要的括号则返回NO。一开始没有考虑到同等大小的左右括号必须相互匹配,循环判断了每种括号,但是每一种括号都可行不代表总体可行。
②改进:字符串读入尽量用scanf("%s"),不要一个一个读。读题时首先读限制条件,往往限制条件中保存着特殊情况和从小归大的方法。
(2)做题

#include<cstdio> #include<iostream> #include<stack> using namespace std; char c[2000000]; int n; int main(){ scanf("%d",&n); if(n==0){ printf("YES\n"); return 0; } scanf("%s",c+1); stack<char> s; for(int i=1;i<=n;i++){//处理每个字母 char nowChar=c[i]; if(s.size()==0){ if(nowChar>=97){ printf("NO\n"); return 0; } s.push(nowChar); }else{ if(nowChar<97){//大写字母直接入栈 s.push(nowChar); }else{//判断上一个大写字母是否与自己匹配 char lastChar=s.top(); if(lastChar+32==nowChar){//匹配 s.pop(); }else{ printf("NO\n"); return 0; } } } } if(s.size()!=0){ printf("NO\n"); return 0; } printf("YES\n"); return 0; }
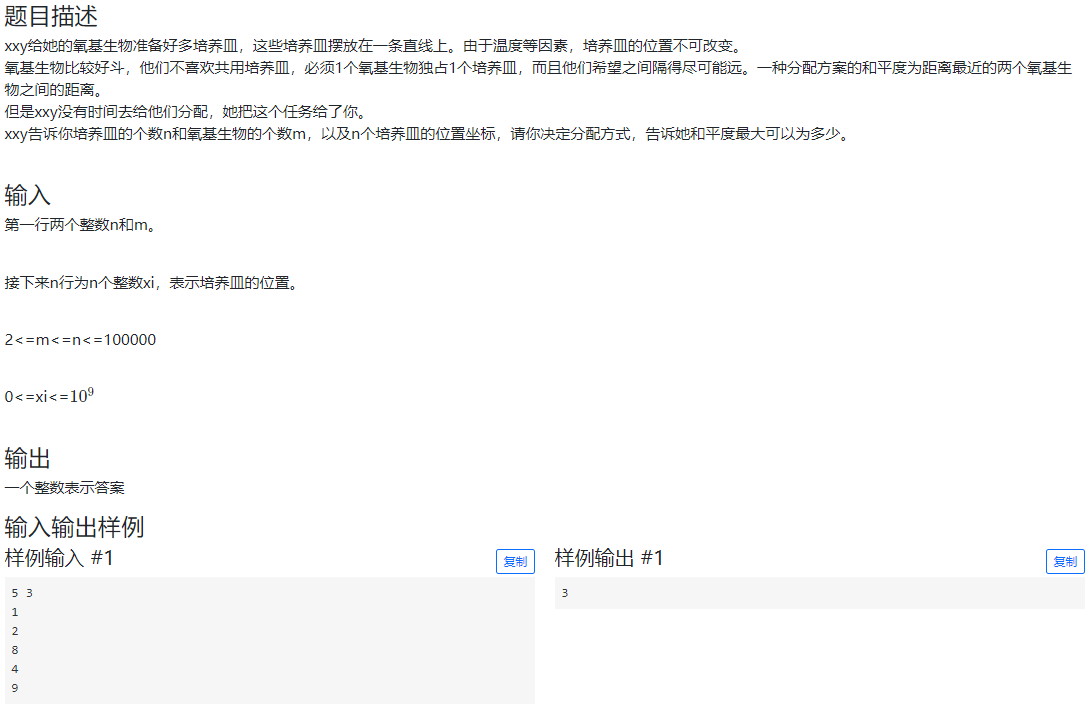
2.问题 C: 又是氧基生物
(1)读题
一开始考虑DP,发现不可行,果断放弃。注意到n、m的范围只有1e5,如果二分xi的话,O(nlogxi),能过。
(2)做题
写了二分之后硬是卡不过去,开了各种优化后减少了半秒,最后强行卡过去了。

#pragma once//只编译一次 #pragma GCC diagnostic error "-std=c++11" #pragma GCC target("avx") #pragma GCC optimize(3) #pragma GCC optimize(3,"Ofast","inline") #pragma GCC optimize("Ofast") #pragma GCC optimize("inline") #pragma GCC optimize("-fgcse") #pragma GCC optimize("-fgcse-lm") #pragma GCC optimize("-fipa-sra") #pragma GCC optimize("-ftree-pre") #pragma GCC optimize("-ftree-vrp") #pragma GCC optimize("-fpeephole2") #pragma GCC optimize("-ffast-math") #pragma GCC optimize("-fsched-spec") #pragma GCC optimize("unroll-loops") #pragma GCC optimize("-falign-jumps") #pragma GCC optimize("-falign-loops") #pragma GCC optimize("-falign-labels") #pragma GCC optimize("-fdevirtualize") #pragma GCC optimize("-fcaller-saves") #pragma GCC optimize("-fcrossjumping") #pragma GCC optimize("-fthread-jumps") #pragma GCC optimize("-funroll-loops") #pragma GCC optimize("-fwhole-program") #pragma GCC optimize("-freorder-blocks") #pragma GCC optimize("-fschedule-insns") #pragma GCC optimize("inline-functions") #pragma GCC optimize("-ftree-tail-merge") #pragma GCC optimize("-fschedule-insns2") #pragma GCC optimize("-fstrict-aliasing") #pragma GCC optimize("-fstrict-overflow") #pragma GCC optimize("-falign-functions") #pragma GCC optimize("-fcse-skip-blocks") #pragma GCC optimize("-fcse-follow-jumps") #pragma GCC optimize("-fsched-interblock") #pragma GCC optimize("-fpartial-inlining") #pragma GCC optimize("no-stack-protector") #pragma GCC optimize("-freorder-functions") #pragma GCC optimize("-findirect-inlining") #pragma GCC optimize("-fhoist-adjacent-loads") #pragma GCC optimize("-frerun-cse-after-loop") #pragma GCC optimize("inline-small-functions") #pragma GCC optimize("-finline-small-functions") #pragma GCC optimize("-ftree-switch-conversion") #pragma GCC optimize("-foptimize-sibling-calls") #pragma GCC optimize("-fexpensive-optimizations") #pragma GCC optimize("-funsafe-loop-optimizations") #pragma GCC optimize("inline-functions-called-once") #pragma GCC optimize("-fdelete-null-pointer-checks") #include<cstdio> #include<iostream> #include<algorithm> using namespace std; int a[200000]; int n,m; //1 2 4 8 9 inline bool isOk(int val){//当前和平度能否达到 int okCnt=0; for(int i=1;i<=n;i++){ //每次贪心到达能满足和平度的点 for(int j=i+1;j<=n;j++){//下一个 if(a[j]-a[i]<val){////如果不满足和平度 //printf("不满足:a[%d]-a[%d]=%d\n",j,i,a[j]-a[i]); continue; } //printf("满足:a[%d]-a[%d]=%d\n",j,i,a[j]-a[i]); i=j-1;//如果满足和平度就转移 okCnt++; break; } } if(okCnt+1<m)return false; return true; } int main(){ scanf("%d%d",&n,&m); int maxx=-1; for(int i=1;i<=n;i++){ scanf("%d",&a[i]); } sort(a+1,a+n+1);//从小到大排序 for(int i=2;i<=n;i++){ maxx=max(maxx,a[i]-a[i-1]); } int l=1,r=maxx; while(l!=r){ if(l==r-1){ if(isOk(r))l=r; else r=l; } int mid=(l+r)/2; if(isOk(mid)){ l=mid; //printf("isOk(%d):true\n",mid); }else{ //printf("isOk(%d):false\n",mid); r=mid; } //printf("l:%d,r:%d\n",l,r); } printf("%d\n",l); //printf("l:%d,r:%d\n",l,r); return 0; }
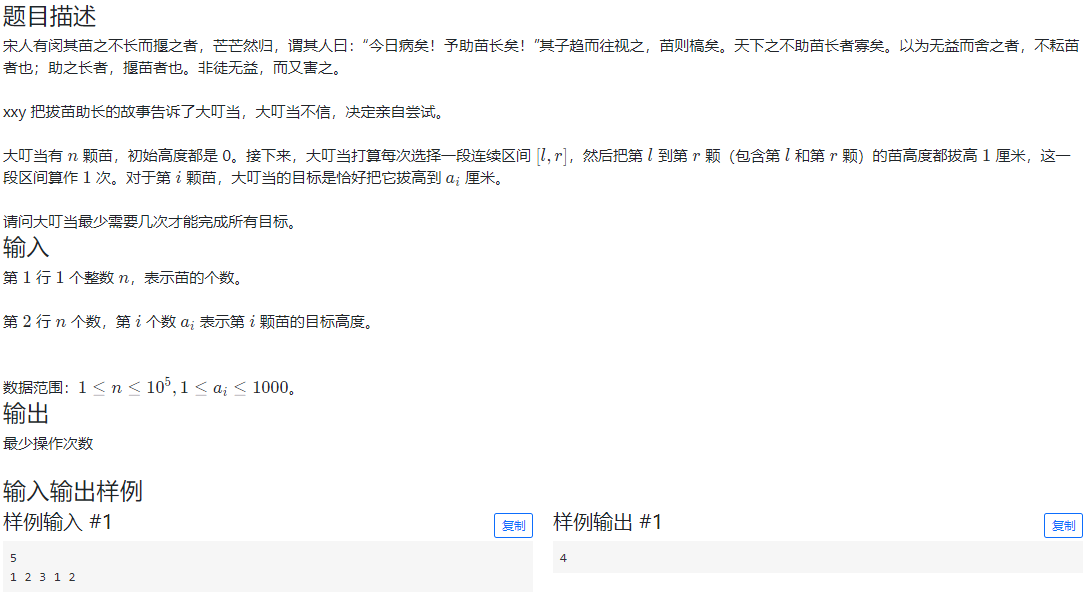
3.问题 B: 拔苗助长
(1)读题
一开始从线段操作联想到线段树了,但不可做。从n的范围来看应当是dp。从ai的数据范围看,可能跟O(na)有关,即从目标高度开始考虑,但是不论怎么做最终复杂度都是超限的。
正确的做法与ai的大小无关,为O(n)算法。考虑到对于每个大于1的序列,贪心地减去最小值,序列就会分成几个被0分割的子序列,可以用递归操作这些子序列,直到求出答案。
那么转化一下,首先思考一个子问题:给定一个序列,其中的值都为正整数且单调递增,怎么减才能最终都减到0?答案很简单,贪心的从最小值开始减,每次影响的范围尽量大。
对于这个题,我们要做的就是将大问题转化为子问题。观察数列性质,发现对于一个单调递增的子数列,如果强制拿出这段子序列,那么很容易通过右边值与左边值的差意识到
减少的总数量(因为每次只能减少1,这一点很关键)。那么对于数列1 2 3,需要的次数就是3次(1-0也算一次),那么如果另一个序列与这个序列无关,但也单调递增,那么另一个序列也满足这个性质。
接下来,总问题就转化成了如何将整个序列的答案转化到若干个子序列中。
换句话说,在扫的过程中,如何计算序列之间分界点的贡献?
枚举子情况。如果是从大到小,比如(3,0),显然两序列完全无关,不需要转化贡献。在另一种情况下,如果是(3,1),表面看1与之前的1存在序列重复性,不能进行转化。
但其实这种情况下,1已经被贪心地 从前面强行减过了。换句话讲,每次减少的实际上是尽量大的范围,即这种情况已被提前计入答案。
(2)做题

#include<cstdio> #include<iostream> using namespace std; int a[200000]; int main(){ int n; scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d",&a[i]); } int ans=0; for(int i=1;i<=n;i++){ if(a[i]>a[i-1]){ ans+=a[i]-a[i-1]; } } printf("%d\n",ans); return 0; }
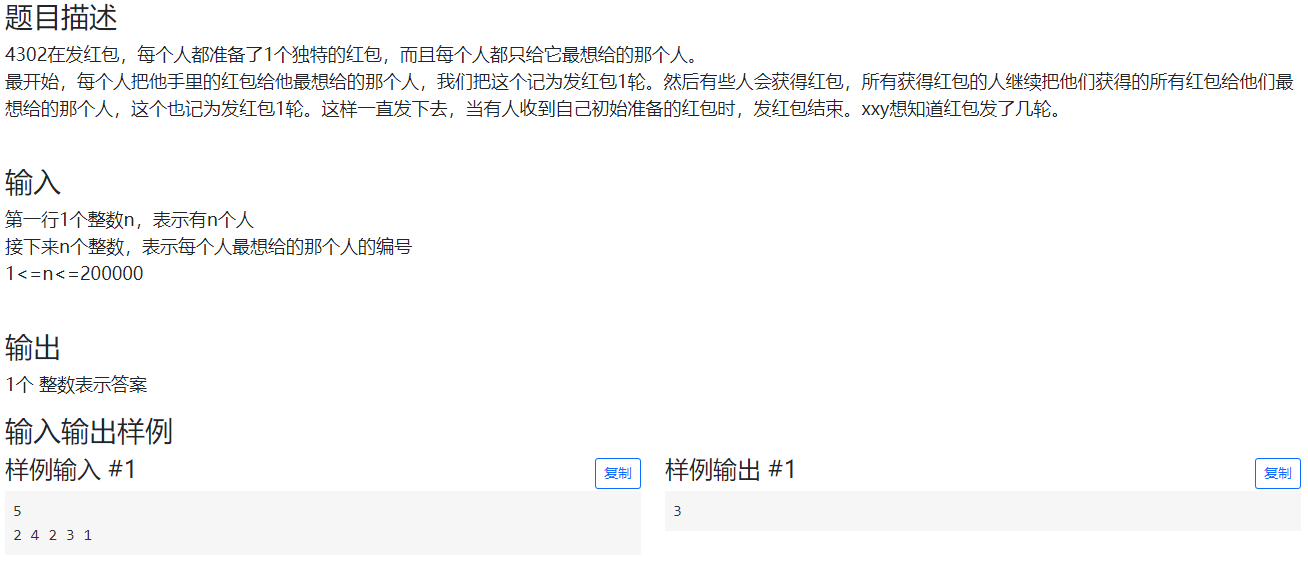
4.问题 D: 发红包
(1)读题
最不正常的地方是只给1个红包。从这里入手,我们考虑,是否要建图,将某个人与收到红包的人连上单向边?
从这个角度看的话,是过不了n=2e5的数据的,换句话讲,需要O(n)的做法。
其次不正常的地方是收到自己初始准备的红包,这里必然是解题的关键区域。
结合两个不正常的地方,能否做一种算法,在图上进行操作,然后判断树的深度?
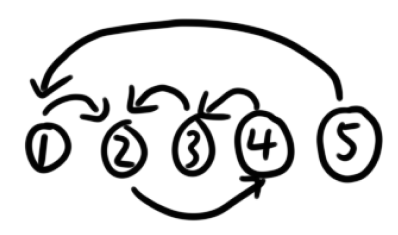
经过画图发现,真正对答案有贡献的只有那些点双连通分量。此时,问题转化为求图中最小的点连通分量的siz。
但是这里有个问题:虽然点双连通具有必要性,但是枚举最小的分量大小是否具有作为答案的充分性?
这个问题可以由单向边的性质回答。由于一个点的出度只有1,那么在某个双连通分量中,其必然是无穷多的"单恋",那么最终只能形成一个简单环,问题也就证明完毕了。
(2)做题
#include<cstdio> #include<iostream> using namespace std; int f[200000+5],d[200000+5],minn,n; int fa(int x){ if(f[x]!=x){ int last=f[x]; f[x]=fa(f[x]); d[x]=d[x]+d[last]; } return f[x]; } void check(int a,int b){ int x=fa(a);int y=fa(b); if(x!=y){ f[x]=y; d[a]=d[b]+1; }else{ minn=min(minn,d[a]+d[b]+1); } } int main(){ cin>>n; for(int i=1;i<=n;i++){ f[i]=i; } minn=2000000000; int temp; for(int i=1;i<=n;i++){ scanf("%d",&temp); check(i,temp); } printf("%d\n",minn); return 0; }




