一、整体流程
1006思考时间过长，导致其他题目思考时间不足。思考不出应当及时止损。
二、具体题目
1.1004 Primality Test
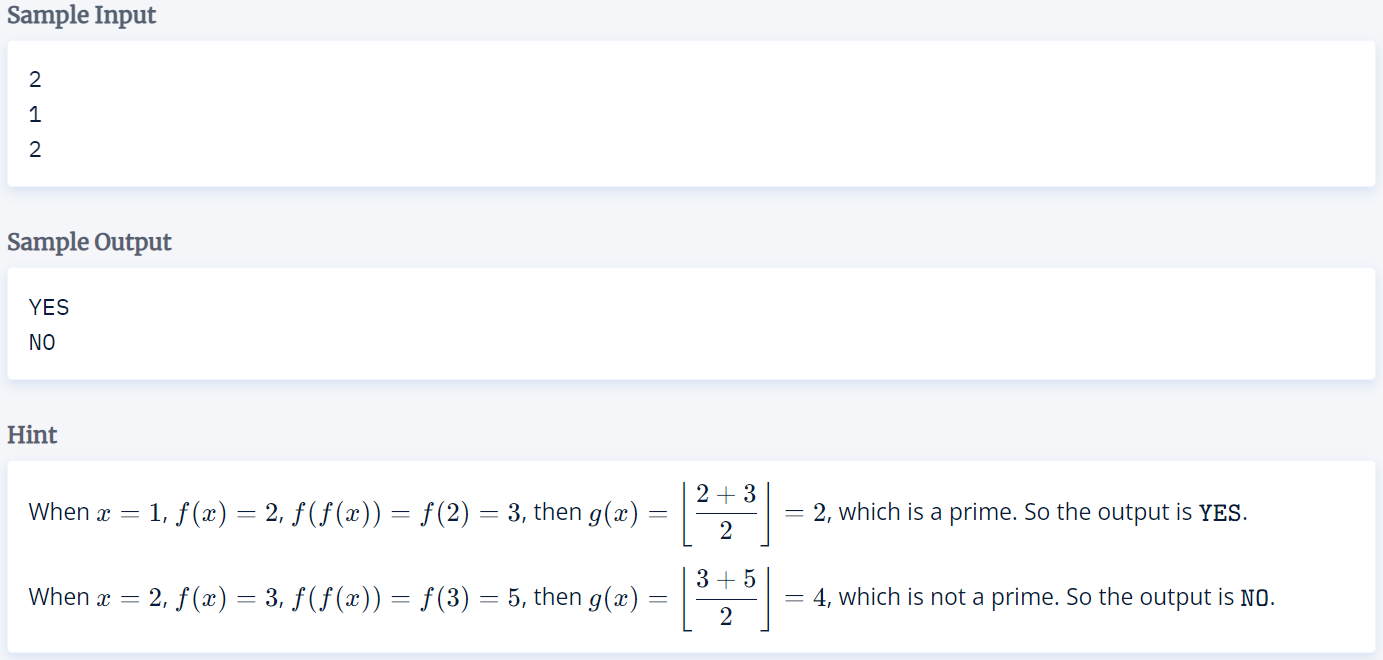
(1)读题：
①场上：读完题后想到了素数筛和Miller-Rabin，TLE。但从式子的特殊性来看，应当能化简公式，并有O(1)做法。但最终没有化简出来。
②改进：一般最简单的一道题都可以和进行转化，缩小程序范围。对于本题，在x>10的情况下，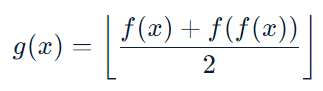
中的f(x)和f(f(x))都为奇数，即g(x)为奇数，收缩尾数至1 3 5 7 9。考虑到为两数相加后除以二，尾数不可能>=5，收缩至1 3。枚举所有情况，意识到x>10的情况下全部输出"No"，暴力做x<10的情况即可。
③联想：
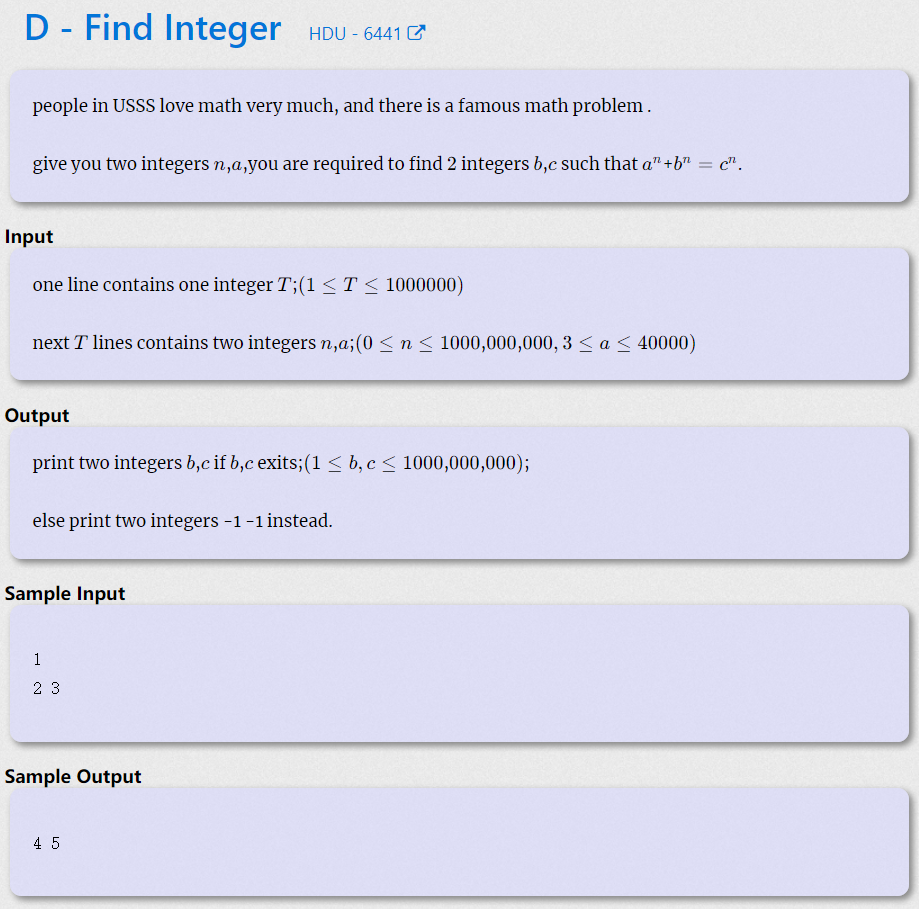
由费马大定理知，n>2的情况下全部输出"-1 -1"。继续做需要知道勾股数定理。
2.1006 Nun Heh Heh Aaaaaaaaaaa
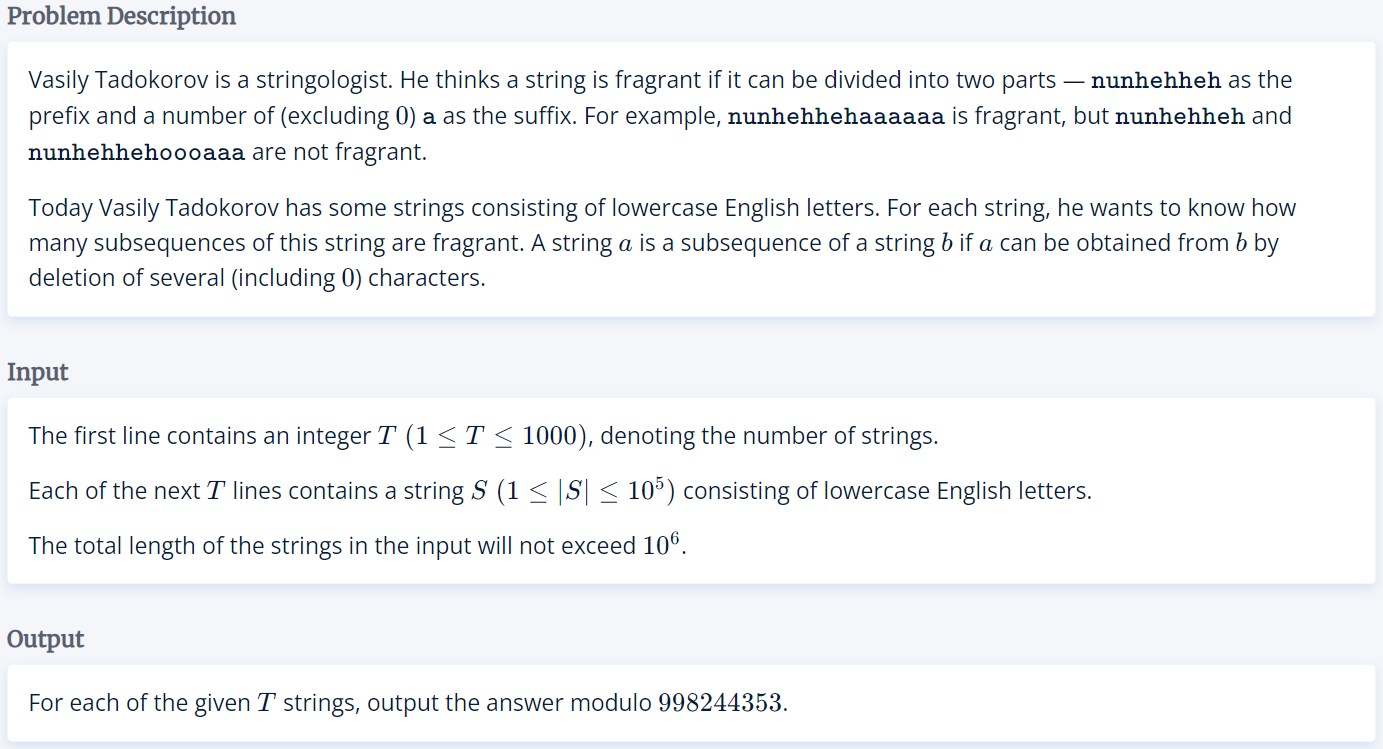
(1)读题：
①场上：场上没算出样例来，一直在算样例。读错题意了，以为只要nunhehheh是前缀，a是后缀就能计算，那么2^(dis(i,j))就是前缀i到后缀j中间的方案量，思考了两个小时，并没有得到正确的解题方法。
②改进：一般完全不可做的题很可能是题意读错了。
3.1011 Jumping Monkey
(1)读题：
①场上：场上完全没思路。
②改进：当没思路时应当思考总问题的子问题。在此题中，从后向前，从答案出发，可以发现值最大的点的答案必然为1。同理，值次大的点的答案必然为2。那么，值第三大的点如何选择呢？这里就要引入“连通块”的概念了
(2)做法：
从末尾开始考虑，每次去掉值最大的点，那么这个点相连的几个连通块都有一个共同的处理：最终必然要跳到即将被去掉的点。
那么去掉这个点后，对每个连通块的值+1，接下来对于每个连通块递归进行此操作即可得到每个点的最大跳跃次数。
可以发现，去掉点的过程整体上形成了一棵树。这棵树的根节点即值最大的点，根节点直接相连的结点即两个连通块分别值最大的点。反向思考，每次枚举当前最小的点，将相连的最大值点作为根，当前连通块即为最优连通块，满足dp无后效性的原理
考虑从下往上建树，那么需要维护的就是：1.连通块的连通性 2.连通块的最大值点 3.判断两点是否联通 4.获取当前剩余点中值最小的点
维护方法：1.并查集 2.并查集数组 3.并查集 4.优先队列
