前置知识:
基本思路:
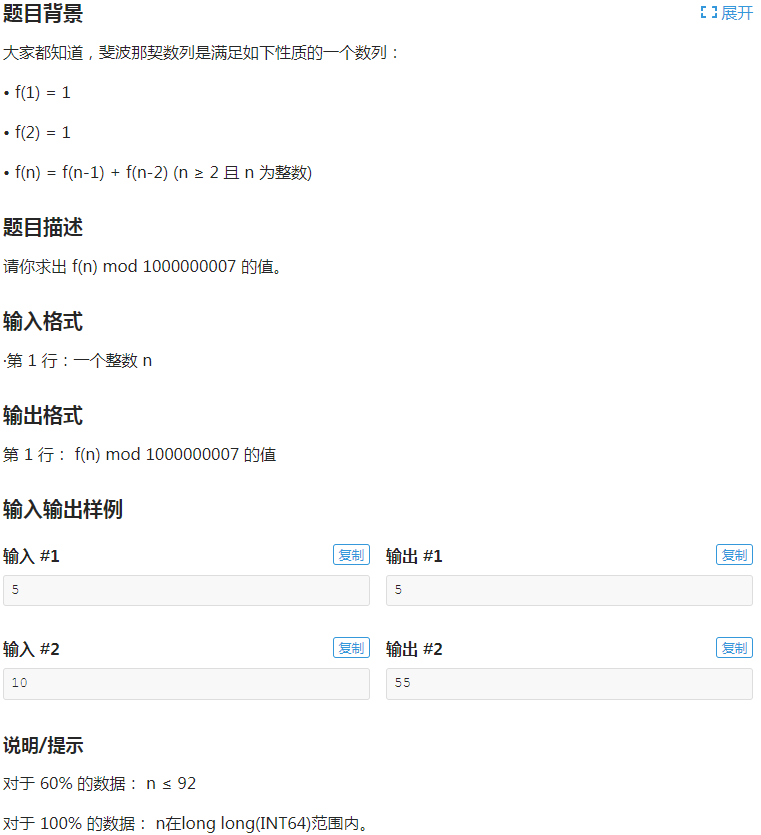
- 要求的转移式为:
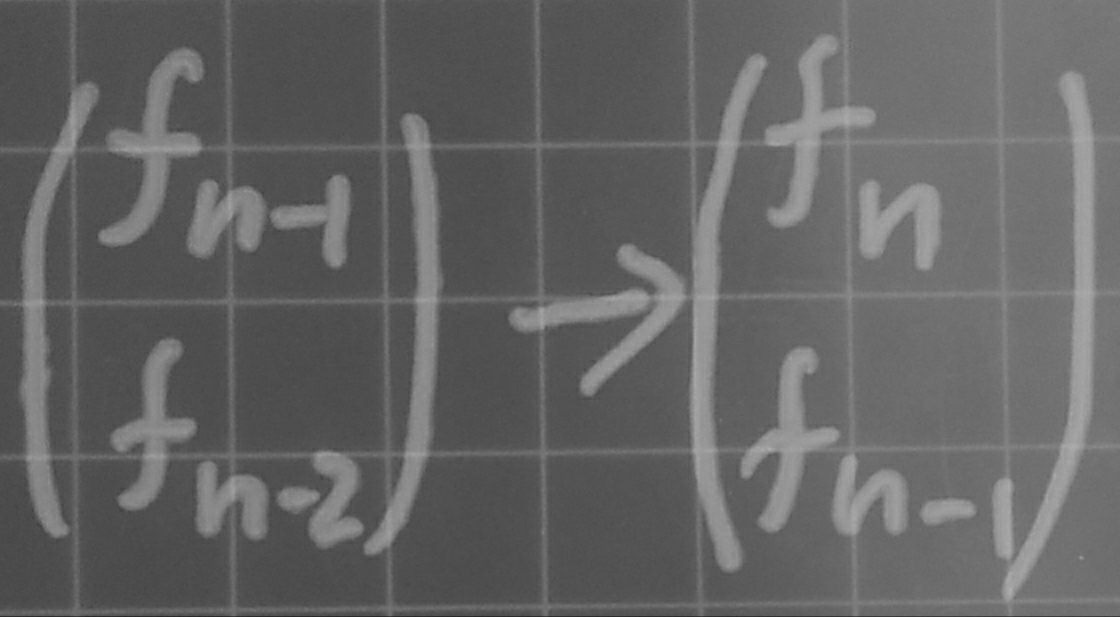 .
.
- 即fn <- 1*fn-1+1*fn-2+,fn-1 <- 1*fn-1+0*fn-2.
- 由矩阵乘法规则可得出转移式:
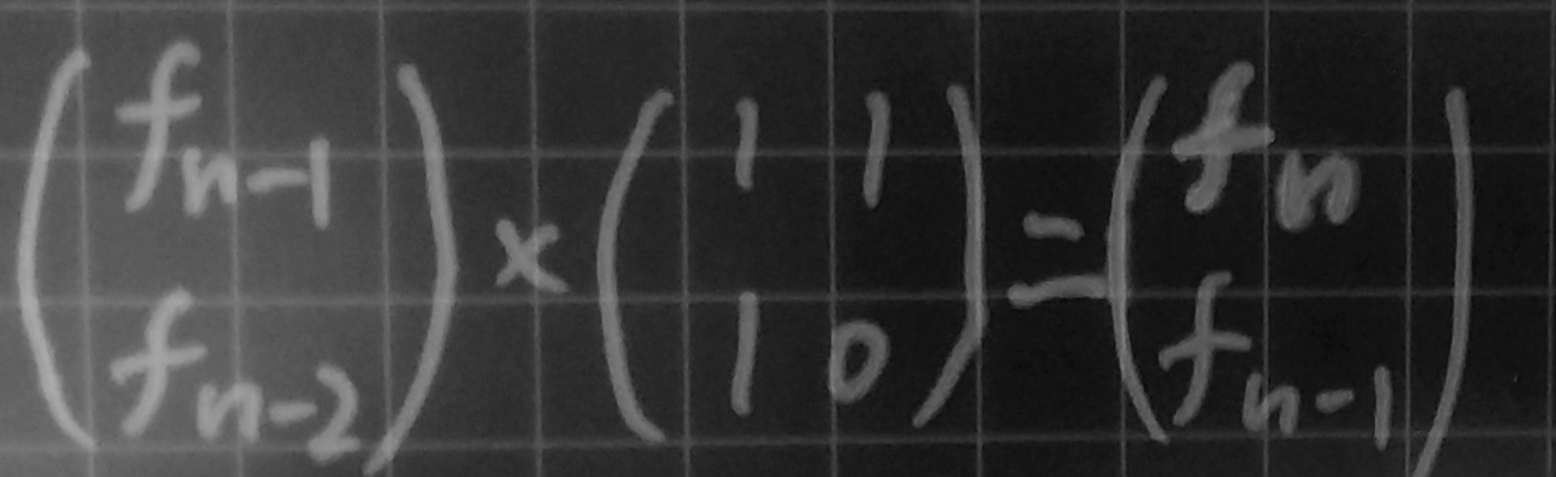 .
. - 再利用快速幂的原理,将乘法规则改为矩阵乘法规则即可.
注意点:
- 开long long.
#include<cstdio>
#include<iostream>
#include<cstring>
#define ll long long
using namespace std;
const int MOD=1000000007;
struct Mat{
ll a[5][5];
int x,y;//行 列数
void init(int x_,int y_){
memset(a,0,sizeof(a));
x=x_,y=y_;
}
};
Mat mull(Mat a,Mat b){
Mat ans;
ans.init(a.x,b.y);
for(int x=1;x<=ans.x;x++){
for(int y=1;y<=ans.y;y++){
for(int k=1;k<=a.y;k++){
ans.a[x][y]=(ans.a[x][y]+a.a[x][k]*b.a[k][y])%MOD;
}
}
}
return ans;
}
Mat poww(Mat a,ll k){
Mat ans;
ans.init(a.x,a.y);
for(int i=1;i<=3;i++)
ans.a[i][i]=1;
Mat tmp=a;
while(k){
if(k&1)ans=mull(ans,tmp);
tmp=mull(tmp,tmp);
k>>=1;
}
return ans;
}
int main(){
ll n;
scanf("%lld",&n);
Mat e;//转换矩阵
e.init(3,3);
e.a[1][1]=1;
e.a[1][2]=1;
e.a[2][1]=1;
e.a[3][2]=1;
Mat basic;//初始矩阵
basic.init(3,1);
basic.a[1][1]=2;
basic.a[2][1]=1;
basic.a[3][1]=1;
Mat ans=poww(e,n-1);
ans=mull(ans,basic);
cout<<ans.a[3][1]<<endl;
return 0;
}



