并查集扩展域的思想:
- 有时,我们需要在使用并查集的同时,表示集合中元素的某些关系(这些关系类似有向边)
- 直接使用并查集显然是不行的,因为并查集只能保证某些元素在或不在同一个集合中,而如果需要表示关系,就不行了
- 这时候就可以尝试扩大关系种类数量的集合数量,比如:给出的元素是1 2 3 4,而此时有两种关系,我们就可以创建三倍的集合(
可能这样描述的不清楚),也就是这样:(1 2 3 4)(1 2 3 4)(1 2 3 4)。而这些数字我们可以储存到同一个数组中,用下标来确定他们所在的集合。由于在默认情况下,不同的集合之间是不会合并的,那么,如果不同的集合之间合并了,就可以代表他们之间有关系(因为我们只在需要表示关系的时候才对不同集合进行合并)
并查集扩展域的实现过程:
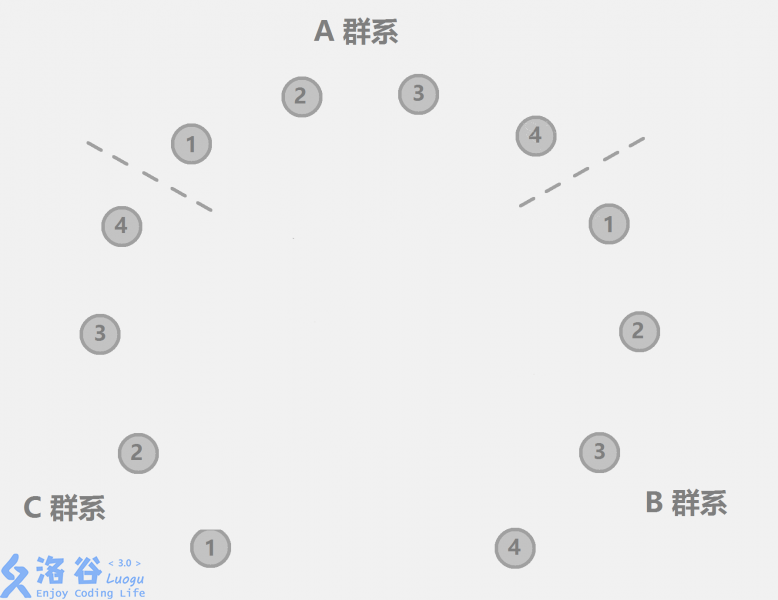
- 初始状态:
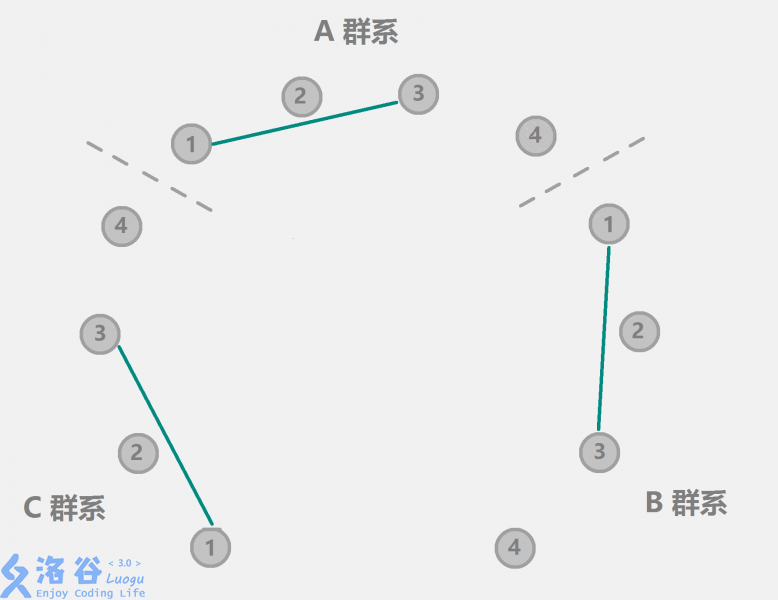
- 普通合并(不表示关系):
- 表示点2与点4之间存在关系(图中红线代表有向边,我们具体实现的话,就把红线两边的点直接进行合并即可。由于当我们查询两个点是否在一个集合时,只会在A群系中查询,所以不会影响普通的查询,只有在查看点2和点4的关系时,我们才会跨群系查询):
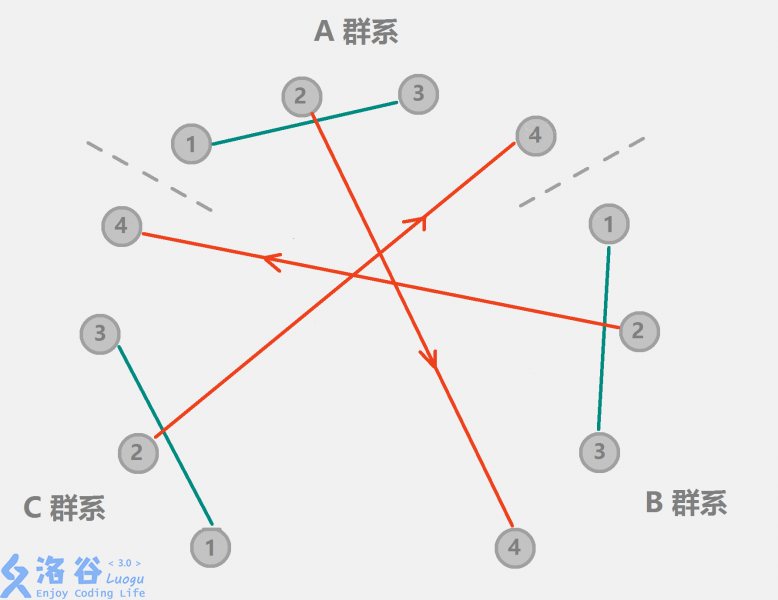
- 接下来的过程同理。根据需要进行同群系或跨群系合并即可。
题目链接:https://www.luogu.org/problemnew/show/P2024
#include<cstdio>
#include<iostream>
using namespace std;
int n,fa[100005*5];
int find(int a){
while(a!=fa[a]){
a=fa[a]=fa[fa[a]];
}
return a;
}
void setTL(int x,int y){
fa[find(x)]=find(y);
fa[find(x+n)]=find(y+n);
fa[find(x+2*n)]=find(y+2*n);
}
void setChi(int x,int y){
fa[find(x)]=find(y+n);
fa[find(x+n)]=find(y+2*n);
fa[find(x+2*n)]=find(y);
}
int main(){
int k;
scanf("%d%d",&n,&k);
for(int i=1;i<=n*4;i++){
fa[i]=i;
//fa[n+i]=n+i;
//fa[2*n+i]=2*n+i;
}
int jhsum=0;
for(int i=1;i<=k;i++){
int a,x,y;
scanf("%d%d%d",&a,&x,&y);
if(x>n||y>n){
jhsum++;continue;
}
if(a==2)if(find(x)==find(y)){//如果x和y是同类
jhsum++;continue;
}
if(a==1){
if(find(x)==find(n+y)||find(x)==find(2*n+y)){
jhsum++;continue;
}
setTL(x,y);
}else if(a==2){
if(find(x)==find(y+2*n)){
jhsum++;continue;
}
setChi(x,y);
}
}
printf("%d\n",jhsum);
return 0;
}
欢迎加入我们的OI讨论群
群号:849352599