|
|
|
|
|
|
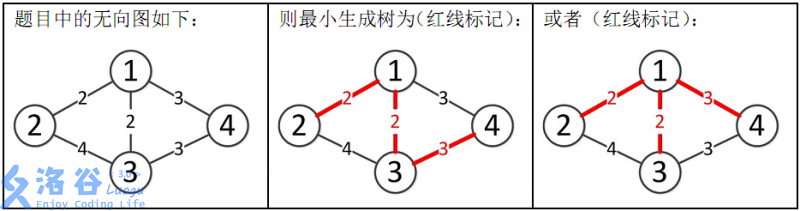
证明过程:
- 首先,假设我们已经对所有边进行了排序,并且当前遍历到的边是连接点1和点2的边
- 因为这条边是最小的边,而点1和点2在最小生成树中一定会直接或间接的相连,因此任何从点1到点2的路径都不小于这条边。如图,如果不走这条边就只能走1→3→2(而如果这样走显然会使得1→2的距离过大,而我们当前只讨论1→2的最优选项)。或者,我们可以假设一种情况:点1和点2之间有两条权值为0.5的边,间接的连接了点1和点2,那么这条路径显然比当前权值为2的边的权值小。但是我们是从小到大遍历边的,所以如果出现了这种情况,那么由于比权值为2的这条边小,那么他们必定已经被遍历。
- 由于那条路径已经被遍历过,那么这时候点1和点2就处于一个并查集了,也就是说我们不会再选择边权为2的这条边了。
- 因此我们可以证明出一个结论:图中权值最小的这条边必然要被选择。
- 假设我们已经选择了直接连接点1和点2的这条边,那么我们就可以对点1和点2进行缩点,由于最小生成树的性质(只要有路径连接两个任意结点即可),缩点对建图没有任何影响。
- 重复以上操作,直到边的数量等于点的数量减一(一个图的最小生成树的边的数量必定等于这个图的点的数量减一)即可得出最小生成树。
拓展资料:
|
|

