一、基础概念
1.DAG
-
有向无环图
2.入度
-
从其他点到特定一个点(也就是说有方向)的连接的边的数量
3.连通图
- 如果图中任意两点都是连通的,那么图被称作连通图
4.双连通分量(连通块):
- 一个无向图中的每一个极大点双连通子图称作此无向图的点双连通分量
5.边集
- 边的集合。
6.二分图
- 设G=(V,E)是一个图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图
二、二分图
1.二分图的判定:
- 当且仅当图中不存在奇环(长度为奇数的环)
2.二分图-匹配:
- "任意两条边都没有公共端点"的边的集合被称为图的一组匹配
3.二分图-最大匹配:
- 包含边数最多的一组匹配
4.二分图-增广路:
- 存在连接两个非匹配点的路径path,使得非匹配边与匹配边在path上交替出现,则pah为匹配S的增广路
5.二分图-最大匹配:
- 匹配S是最大匹配,当且仅当图中不存在S的增广路
- 定理:G的最大独立集的大小等于n减去最大匹配数
6.二分图-匈牙利算法:
- 复杂度O(mn)
7.二分图-完备匹配:
- 给定一张左、右结点数均为N的二分图,则包含N条边的一组匹配称为完备匹配
8.二分图-独立集:
- "任意两点都没有边相连"的点集
9.二分图-最大独立集:
- 包含点数最多的独立集
10.二分图-团:
- "任意两点都有一条边相连"的子图
11.二分图-最大团:
- 点数最多的团
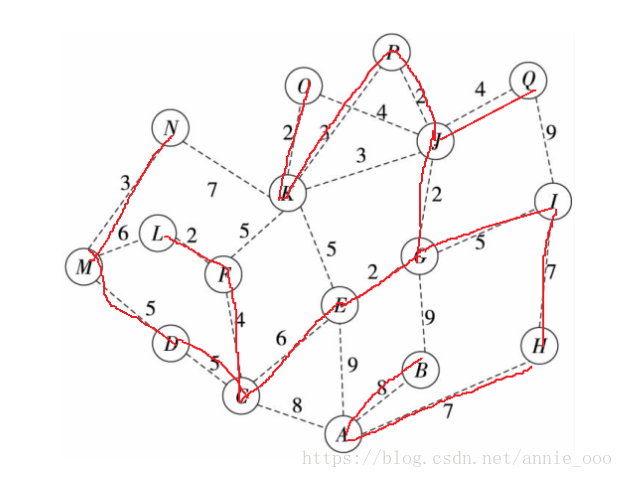
三、最短路径
1.最短路径生成树
- 任意一对父子结点都满足 dist[y]=dist[x]+z 的树结构称为图的一颗最短路径生成树
2.最短路径生成树与最小生成树区别
- 最小生成树优先考虑整体最小,而最短路径生成树只考虑路径最小
-
最短路径生成树 -
最小生成树