题目描述
阿米巴是小强的好朋友。
阿米巴和小强在草原上捉蚂蚱。小强突然想,如果蚂蚱被他们捉灭绝了,那么吃蚂蚱的小鸟就会饿死,而捕食小鸟的猛禽也会跟着灭绝,从而引发一系列的生态灾难。
学过生物的阿米巴告诉小强,草原是一个极其稳定的生态系统。如果蚂蚱灭绝了,小鸟照样可以吃别的虫子,所以一个物种的灭绝并不一定会引发重大的灾难。
我们现在从专业一点的角度来看这个问题。我们用一种叫做食物网的有向图来描述生物之间的关系:
一个食物网有N个点,代表N种生物,如果生物x可以吃生物y,那么从y向x连一个有向边。
这个图没有环。
图中有一些点没有连出边,这些点代表的生物都是生产者,可以通过光合作用来生存; 而有连出边的点代表的都是消费者,它们必须通过吃其他生物来生存。
如果某个消费者的所有食物都灭绝了,它会跟着灭绝。
我们定义一个生物在食物网中的“灾难值”为,如果它突然灭绝,那么会跟着一起灭绝的生物的种数。
举个例子:在一个草场上,生物之间的关系是:
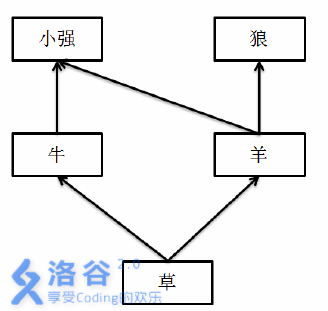
如果小强和阿米巴把草原上所有的羊都给吓死了,那么狼会因为没有食物而灭绝,而小强和阿米巴可以通过吃牛、牛可以通过吃草来生存下去。所以,羊的灾难值是1。但是,如果草突然灭绝,那么整个草原上的5种生物都无法幸免,所以,草的灾难值是4。
给定一个食物网,你要求出每个生物的灾难值。
输入输出格式
输入格式:
输入文件 catas.in 的第一行是一个正整数 N,表示生物的种数。生物从 1 标
号到 N。
接下来 N 行,每行描述了一个生物可以吃的其他生物的列表,格式为用空
格隔开的若干个数字,每个数字表示一种生物的标号,最后一个数字是 0 表示列
表的结束。
输出格式:
输出文件catas.out包含N行,每行一个整数,表示每个生物的灾难值。
输入输出样例
输入样例#1:
5 0 1 0 1 0 2 3 0 2 0
输出样例#1:
4 1 0 0 0
说明
【样例说明】
样例输入描述了题目描述中举的例子。
【数据规模】
对50%的数据,N ≤ 10000。
对100%的数据,1 ≤ N ≤ 65534。
输入文件的大小不超过1M。保证输入的食物网没有环。
个人思路:
- 拆点、合并(通过LCA1)后进行拓扑排序
-

拆点 -
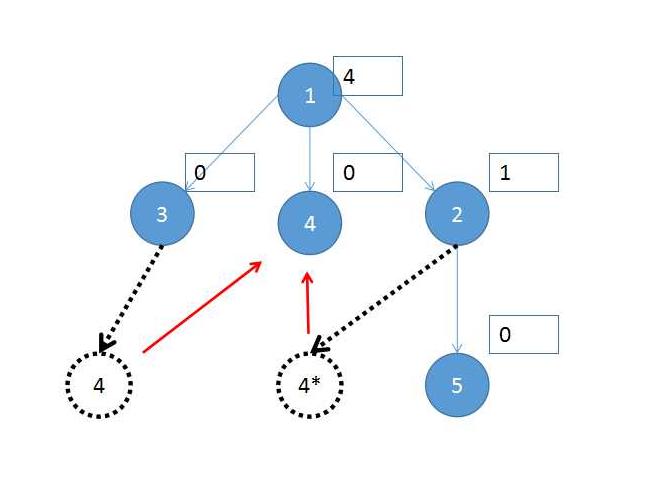
合并
题目地址:https://www.luogu.org/problemnew/show/P2597
#include <cstdio>
#include <queue>
#include <cstring>
#include <iostream>
#define sz 31
#define N 65540
using namespace std;
int tot,nxt[N*4],point[N*4],v[N*4],tot1,nxt1[N*4],point1[N*4],v1[N*4],tot2,nxt2[N*4],point2[N*4],v2[N*4],n,in[N],ran[N],h[N];
int f[N][sz],ans[N];
void addline(int x,int y){++tot; nxt[tot]=point[x]; point[x]=tot; v[tot]=y;}
void addline1(int x,int y){++tot1; nxt1[tot1]=point1[x]; point1[x]=tot1; v1[tot1]=y;}
void addline2(int x,int y){++tot2; nxt2[tot2]=point2[x]; point2[x]=tot2; v2[tot2]=y;}
void topsort()
{
queue<int>q;
for (int i=1;i<=n;i++)
if (!in[i]) q.push(i);
int num=0;
while (!q.empty())
{
int now=q.front(); q.pop();
ran[++num]=now;
for (int i=point[now];i;i=nxt[i])
{
in[v[i]]--;
if (!in[v[i]]) q.push(v[i]);
}
}
}
int lca(int x,int y)
{
if (h[x]<h[y]) swap(x,y);
int k=h[x]-h[y];
for (int i=0;i<sz;i++)
if ((k>>i)&1) x=f[x][i];
if (x==y) return x;
for (int i=sz-1;i>=0;i--)
if (f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
return f[x][0];
}
void dfs(int now)
{
for (int i=point2[now];i;i=nxt2[i])
{
dfs(v2[i]);
ans[now]+=ans[v2[i]];
}
ans[now]++;
}
int main()
{
int i,j;
scanf("%d",&n);
for (i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
while (x) {in[i]++;addline1(i,x);addline(x,i);scanf("%d",&x);}
}
topsort();
for (i=1;i<=n;i++)
{
int x=v1[point1[ran[i]]];
for (j=point1[ran[i]];j;j=nxt1[j])
x=lca(x,v1[j]);
addline2(x,ran[i]);
h[ran[i]]=h[x]+1;
f[ran[i]][0]=x;
for (j=1;j<sz;j++) f[ran[i]][j]=f[f[ran[i]][j-1]][j-1];
}
dfs(0);
for (i=1;i<=n;i++) printf("%d\n",ans[i]-1);
}



