P1526 [NOI2003]智破连环阵 [搜索+剪枝(二分图)]

$[NOI2003]智破连环阵$

在坐标轴第一象限中有 $M$ 个武器, $N$ 个炸弹, 每个武器按顺序开启 可被摧毁状态, 以下简称 $B$ 状态, 若一个武器在炸弹的爆炸范围内, 则这个武器将被摧毁, 紧接着下一个武器将会开启 $B$ 状态.

要求安排炸弹的爆炸顺序, 使得摧毁全部武器使用的炸弹最小 .

$M, N \le 100$ .

---

$\color{blue}{最初想法}$

搜索? 直接退火就好了… 爆炸 .代码纪念 .

---

$\color{red}{正解部分}$

一个炸弹摧毁的一定是连续的一段区间, 所以整个武器序列可分为几段, 每段被都某个炸弹摧毁 .

设当前 $DFS$ 到的区间右端点为 $r$, 划分了 $cnt$ 个区间,

预处理出 $Max\_t[i,j]$ 表示 $i$ 炸弹从 $j$ 武器开始炸起, 所能炸到的最右端点,
不难得出状态转移式 $Max\_t[i,j] = \max(Max\_t[i,j+1], j)$ .

但是我们现在想要知道的是炸掉武器 $[i, M]$ 需要炸弹的下界, 便于剪枝,
设为 $Min\_cost[i]$, 不考虑炸弹个数的限制,
容易得出状态转移式 $Min\_cost[i]=\min(Min\_cost[Max\_t[j,i] + 1]+1)$ .

若 $cnt+Min\_cost[r] \geq Ans$, 则直接 $return$, 作为一个 最优性剪枝 .

---

于是可以对武器序列的分界点进行搜索, 若一个炸弹可以炸掉一个区间, 则这个炸弹与那个区间连边, 最终得到类下图 $↓$

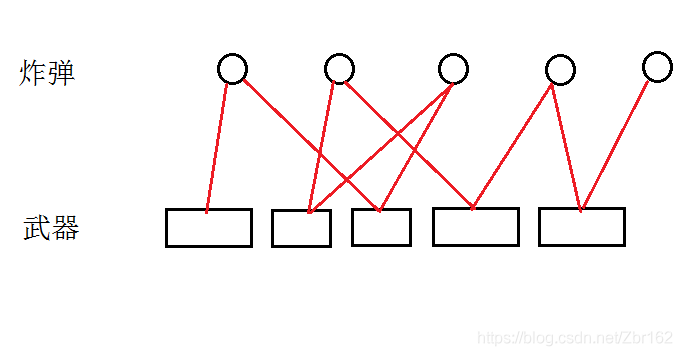
观察可以发现这个图为标准的二分图,于是使用 匈牙利 在 $DFS$ 决策时进行 可行性剪枝 .

$a$炸弹可以和$b$区间连边需要满足的条件为

• 可以完全覆盖这个区间, 即 $Max\_t[a, l_b]>=r_b$ .

---

$\color{red}{实现部分}$

• 匈牙利 可以在 $DFS$ 过程中进行 .
• 注意该倒序循环的不要忘记倒序循环 .
• 注意全局数组会改变 .
• 注意刚开始时需要赋值$Ans$为 $N$, 不能赋值 $inf$, 这样会导致答案得出前 最优性剪枝 失效 .

#include<bits/stdc++.h>
#define reg register

const int maxn = 105;

int M;
int N;
int K;
int Ans;
int mark[maxn];
int Min_cost[maxn];
int Max_t[maxn][maxn];

bool Used[maxn];
bool like[maxn][maxn];

struct Node{ int x, y; } A[maxn], B[maxn];

bool Pd(Node zd, Node wq){
        int t1 = zd.x-wq.x, t2 = zd.y-wq.y;
        return t1*t1 + t2*t2 <= K*K;
}

bool Find(int x){
        for(reg int i = 1; i <= N; i ++)
                if(like[i][x] && !Used[i]){
                        Used[i] = 1;
                        if(!mark[i] || Find(mark[i])){ mark[i] = x; return 1; }
                }
        return 0;
}

void DFS(int k, int cnt){
        if(cnt + Min_cost[k] >= Ans) return ;
        if(k == M+1){ Ans = std::min(Ans, cnt); return ; }
        int Tmp_1[maxn];
        for(reg int i = k; i <= M; i ++){
//                memcpy(Tmp_1, mark, sizeof Tmp_1);
                for(reg int j = 1; j <= N; j ++){
                        Tmp_1[j] = mark[j];
                        if(Max_t[j][k] >= i) like[j][cnt+1] = 1; 
                }
                
                memset(Used, 0, sizeof Used);
                if(Find(cnt+1)) DFS(i+1, cnt+1);

                for(reg int j = 1; j <= N; j ++){
                	mark[j] = Tmp_1[j];
                        if(Max_t[j][k] >= i) like[j][cnt+1] = 0;
                }
//                memcpy(mark, Tmp_1, sizeof mark);
        }
}

int main(){
        scanf("%d%d%d", &M, &N, &K);
        for(reg int i = 1; i <= M; i ++) scanf("%d%d", &A[i].x, &A[i].y);
        for(reg int i = 1; i <= N; i ++) scanf("%d%d", &B[i].x, &B[i].y);
        for(reg int i = 1; i <= N; i ++)
                for(reg int j = M; j >= 1; j --)
                        if(Pd(B[i], A[j])) Max_t[i][j] = std::max(Max_t[i][j+1], j);
        memset(Min_cost, 0x3f, sizeof Min_cost);
        Min_cost[M+1] = 0;
        for(reg int i = M; i >= 1; i --)
                for(reg int j = 1; j <= N; j ++)
                        if(Pd(B[j], A[i]))
                                Min_cost[i] = std::min(Min_cost[i], Min_cost[Max_t[j][i] + 1] + 1);
        Ans = N;
        DFS(1, 0);
        printf("%d\n", Ans);
        return 0;
}