5696. 统计异或值在范围内的数对有多少

5696. 统计异或值在范围内的数对有多少

难度困难3收藏分享切换为英文接收动态反馈

给你一个整数数组 nums （下标 从 0 开始 计数）以及两个整数：low 和 high ，请返回 漂亮数对 的数目。

漂亮数对 是一个形如 (i, j) 的数对，其中 0 <= i < j < nums.length 且 low <= (nums[i] XOR nums[j]) <= high 。

示例 1：

输入：nums = [1,4,2,7], low = 2, high = 6
输出：6
解释：所有漂亮数对 (i, j) 列出如下：
    - (0, 1): nums[0] XOR nums[1] = 5 
    - (0, 2): nums[0] XOR nums[2] = 3
    - (0, 3): nums[0] XOR nums[3] = 6
    - (1, 2): nums[1] XOR nums[2] = 6
    - (1, 3): nums[1] XOR nums[3] = 3
    - (2, 3): nums[2] XOR nums[3] = 5

示例 2：

输入：nums = [9,8,4,2,1], low = 5, high = 14
输出：8
解释：所有漂亮数对 (i, j) 列出如下：
    - (0, 2): nums[0] XOR nums[2] = 13
    - (0, 3): nums[0] XOR nums[3] = 11
    - (0, 4): nums[0] XOR nums[4] = 8
    - (1, 2): nums[1] XOR nums[2] = 12
    - (1, 3): nums[1] XOR nums[3] = 10
    - (1, 4): nums[1] XOR nums[4] = 9
    - (2, 3): nums[2] XOR nums[3] = 6
    - (2, 4): nums[2] XOR nums[4] = 5

提示：

• 1 <= nums.length <= 2e4
• 1 <= nums[i] <= 2e4
• 1 <= low <= high <= 2e4

解决方案：

利用字典树统计二进制前缀相同的数字个数。

如：

\[1010\\ 1001\\ 0100\\ 1011\\ \]

上面四个二进制数字中，前缀为 \(1\) 的数字有 \(3\) 个；前缀为 \(101\) 的数字有 \(2\) 个，前缀为 \(0100\) 的数字有一个。

在树中的存储方式如下：

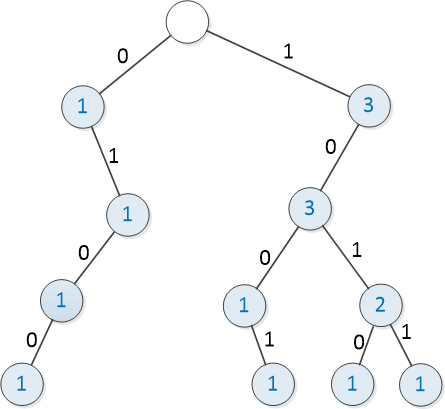
从根节点到叶子节点的路径代表一个二进制数字，结点上的值代表二进制前缀相同的数字个数。

指针实现 trie：

class Trie {
    int cnt;
    Trie *son[2];
public:
    Trie():cnt(0) {
        son[0] = son[1] = NULL;
    }
    void insert(int x) {
        Trie *p = this;
        for (int i = 15; i >= 0; --i) {
            int t = x>>i&1;
            if (!p->son[t]) p->son[t] = new Trie;
            p = p->son[t];
            ++p->cnt;
        }
    }
    int query(int x, int val) {  // 寻找与x异或后大于val的数的个数
        Trie *p = this;
        int ret = 0;
        for (int i = 15; i >= 0; --i) {
            int a = x>>i&1, b = val>>i&1;
            if (b == 0) {
                if (p->son[a^1]) ret += p->son[a^1]->cnt;
                p = p->son[a];
            }
            else {
                p = p->son[a^1];
            }
            if (!p) return ret;
        }
        return ret;
    }
};

class Solution {
public:
    int countPairs(vector<int>& nums, int low, int high) {
        Trie trie;
        for (int num : nums) trie.insert(num);
        int ans = 0;
        for (int num : nums) {
            ans += trie.query(num, low-1) - trie.query(num, high);
            //cout << ans << '#';
        }
        //cout << endl;
        return ans>>1;
    }
};

数组实现trie：

const int N = 1e5;
int tree[N][2], cnt[N];
class Trie {
    int tot = 0;
public:
    Trie() {memset(tree, 0, sizeof tree), memset(cnt,0,sizeof cnt);}
    void insert(int x) {
        int p = 0;
        for (int i = 15; i >= 0; --i) {
            int t = x>>i&1;
            if (!tree[p][t]) tree[p][t] = ++tot;
            p = tree[p][t];
            ++cnt[p];
            //cout << i << '-' << t << ' ' << cnt[p] << endl;
        }
    }
    int query(int x, int val) {  // 寻找与x异或后大于val的数的个数
        int p = 0;
        int ret = 0;
        for (int i = 15; i >= 0; --i) {
            int a = x>>i&1, b = val>>i&1;
            if (b == 0) {
                ret += cnt[tree[p][a^1]];
                p = tree[p][a];
            }
            else {
                p = tree[p][a^1];
            }
            if (p == 0) return ret;
        }
        return ret;
    }
};

class Solution {
public:
    int countPairs(vector<int>& nums, int low, int high) {
        Trie trie;
        for (int num : nums) trie.insert(num);
        int ans = 0;
        for (int num : nums) {
            ans += trie.query(num, low-1) - trie.query(num, high);
            //cout << ans << '#';
        }
        //cout << endl;
        return ans>>1;
    }
};