深度学习笔记(4):1.4-1.5:CNN中常用两大基本操作:padding、strided convolutions
原创起个名字好难.JPG 最后发布于2018-09-18 22:20:34 阅读数 2118 收藏
展开
1.4 padding
在深度学习中,需要学会的一个基本卷积操作就是padding,padding是什么意思呢?
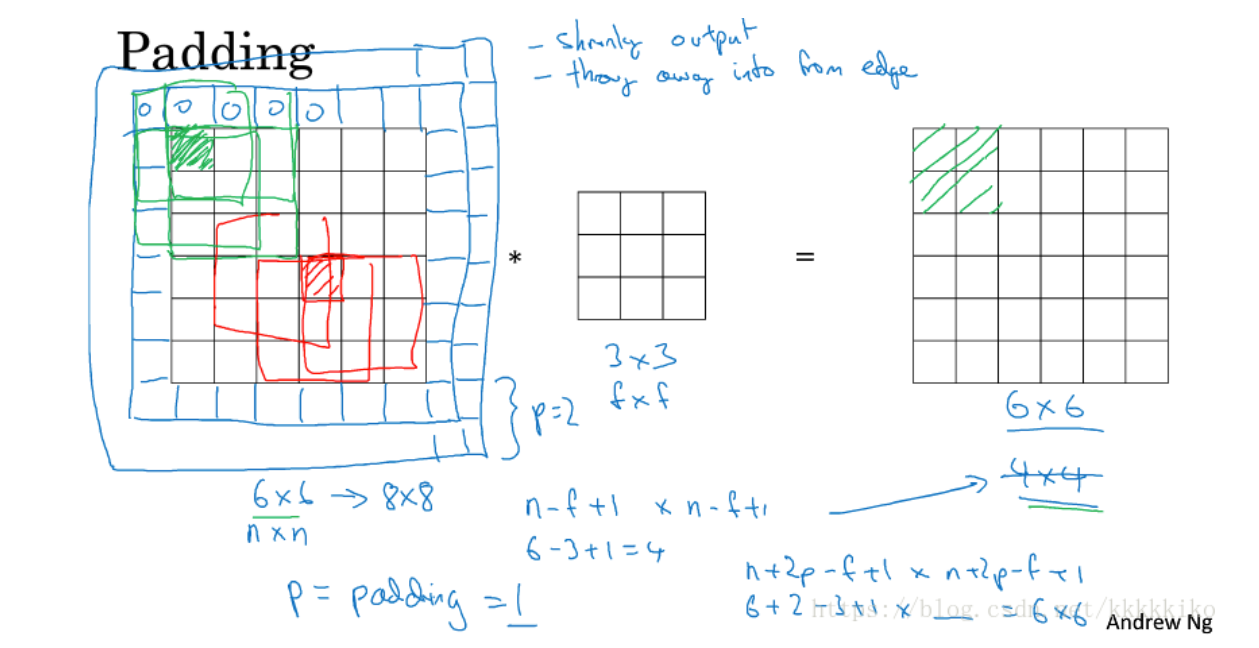
之前未使用padding时,假设我们的图片是6*6的,在使用3*3的filter之后,图片变为4*4的,发现了什么?图片使用卷积操作之后变小了,这还只是使用一次,如果我们在深层网络中需要使用多次呢?可想而知,图片就会变得越来越小,甚至会缩小到1*1,我们当然不希望在识别边缘或其他特征时图片变得越来越小。
除此之外,这样直接使用卷积运算还有一个问题,那就是图片边缘角落的像素信息使用次数较少,这容易使我们损失掉很多处在角落位置的像素带来的信息,怎么说呢?如上图所示,我们本来是6*6的矩阵,左上角即(1,1)位置的格子,那个绿色的格子,在使用3*3的filter进行卷积运算时,我们仅使用一次,这样我们就容易损失掉这一部分包含的信息。
为了解决卷积运算带来的这两种缺点,padding思想被提出。什么是padding呢?padding就是在原图像周围再加上p圈像素,p在这里是参数,像素值我们一般取0。这样一来既不怕图像通过卷积运算变得越来越小,也不怕图像原本边缘处的信息利用不到了。
原来未加像素前,6*6的图片通过3*3的filter我们可以得到4*4的图片,这是有公式的,假设原图像是n*n,filter是f*f,我们稍微一想就知道filter共作了(n-f+1)*(n-f+1)次运算,所以最后得到的图片是(n-f+1)*(n-f+1)。加了一圈像素之后,原图像由6*6变为8*8,注意加了一圈,每行每列都增加了两个,所以加了P圈之后,我们的公式就变为(n+2p-f+1)*(n+2p-f+1),所以,8*8的图片做了卷积之后我们得到6*6的图片,发现了吗?使用完padding之后,我们通过卷积运算就可以得到同原图像大小相同的图片。除此之外,我们再来看原来绿格子的使用情况,发现了什么,绿格子的值通过filter作用于左上方四个格子,因为被使用了四次,边缘信息使用得到了保证。
加入padding的有两种卷积运算,如下图所示:

一种我们称为valid,是指没有使用padding的,即p=0,公式就是未加2p前原始的公式;一种是same,即使用padding后保证图片大小和原图大小相同,这就需要我们计算一下,即n+2p-f+1=n,所以p=(f-1)/2,也是因为这个公式,所以一般filter的f取值我们一般选奇数(odd),3、5、7这样,使用奇数还有一个原因,就是奇数的filter有一个central pixel,而在CV中认为有central pixel是很重要的,便于指出过滤器的位置。
1.5 卷积步长(strided convolutions)
了解了卷积神经网络中常用的padding操作后,我们来看一下另一个卷积神经网络中常用的操作‘卷积步长’是怎么一回事。
‘卷积步长’其实就是在卷积过程中增加了‘步长’这一参数,什么意思呢?见下图:
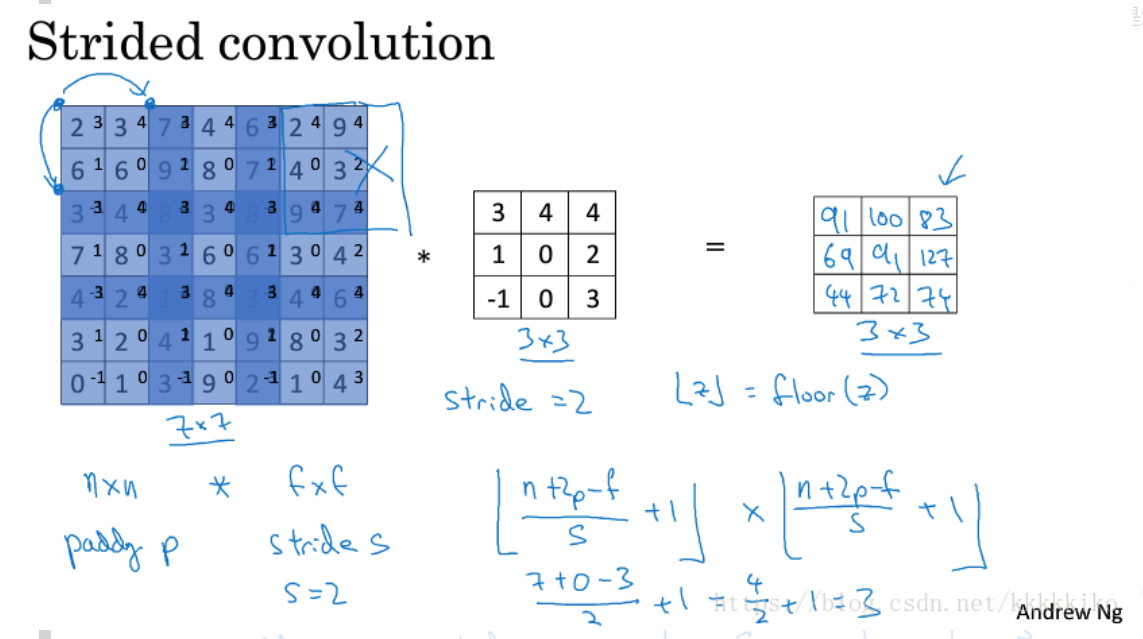
以前我们是默认步长为1进行卷积运算的,即3*3的filter同左上角九宫格进行完运算后向右移动一步再次进行卷积运算,但我们现在不是默认步长为1了,而是将步长设为一个可调节的参数s,当s=2时,每次做完一次卷积运算,filter就向右或向下移动两步,所以就会有上图中的结果,这样做完卷积运算,我们会得到一个3*3的图片,而左图中深蓝色部分表示在整个过程中使用两次的像素值,其他部分均使用一次,可见加入步长这一参数影响后,在不加padding的情况下,其实损失了更多图片的边缘信息。
推导一下公式,我们可以快速得到上图中公式,因为步长不再是1了,所以要先除以s,然后再加1得到卷积后图片的维度为(n+2p-f)/s+1*(n+2p-f)/s+1,但是有个问题,如果(n+2p-f)/s不是整数值怎么办,我们采取的原则是取下整数,运行的思想就是我们要求卷积运算过程中filter必须完全处于图像中或者填充后的图像中,如果有部分图片filter还没接触到,且也不够一整个filter位置,如上图所示那样,假设在最后两列位置对于3*3的filter少了一列,那么这个结果我们就不要了,这就是取下整数的含义。
总结一下如下图所示:

对于n*n的图片,f*f的filter,在加入padding参数p和stride步长s之后,我们的输出图片大小(output size)变为,公式中符号表示取下整数。
最后提一下不同地方使用学术用语的不同之处,如下图所示:
卷积(convolution)在数学书或者是信号处理(signal processing)书中是先要将filter进行两次镜像操作,然后对镜像操作后得到的结果再同原图片进行element-wise乘积求和,所以以此定义的‘卷积’运算具有结合律,而这一特点对一些信号处理来说很有用,同时,数学家们将未翻转直接进行element-wise乘积求和的运算称为cross-correlation而不是convolution,但在深度学习中,我们习惯于将未翻转直接进行element-wise乘积求和的运算称为‘卷积’,因为在深度学习中,我们不需要结合律这个特质,filter是否进行翻转操作对我们的结果没有影响,且不进行翻转也可以简化代码,所以在深度学习中,我们普遍称直接进行element-wise乘积求和的运算为‘卷积’。
版权声明:尊重博主原创文章,转载请注明出处https://blog.csdn.net/kkkkkiko/article/details/82759941
————————————————
版权声明:本文为CSDN博主「起个名字好难.JPG」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/kkkkkiko/article/details/82759941

 浙公网安备 33010602011771号
浙公网安备 33010602011771号