后缀自动机(SAM)奶妈式教程
后缀自动机(SAM)
为了方便,我们做出如下约定:
-
“后缀自动机” (Suffix Automaton) 在后文中简称为 SAM 。
-
记 \(|S|\) 为字符串 \(S\) 的长度。
-
记 \(\sum\) 为字符集,记 \(|\sum|\) 为字符集大小。
关于 SAM 的复杂度证明在 OI Wiki 上已经很全面了,这里只是希望可以帮助大家理解 SAM 是如何工作的以及一些应用,对这些不再多做证明。
在前几个部分中,你只需要跟着笔者给出的构建好的 SAM 图理解某些定义,不需要知道 SAM 为什么像这样。
Part 0 前言
-
马上就要到联赛了,想必再去学习新的算法也已经来不及了吧。
本来以为将近两年的 OI 生涯可以让我学到很多,现在看来也不过如此。
既然这样,不如来一个干脆漂亮的收场:我决定把它作为我,作为一个 OIer 的最后一篇算法学习博客。
它将会是一个大工程。好,我们开始吧——后缀自动机奶妈式教学。
-
笔者认为,OI 是偏向工科的一门学科,比起 “为什么” ,我们更倾向于 “怎么做” 。
譬如一个算法,我们需要了解它是如何工作的,以及它可以解决什么样的问题,而对于它的正确性、时间复杂度的证明往往不太关心。
尤其是对于复杂算法,我们掌握如何应用它们就足够了,至于证明,那是数学家的事情,不是吗?
纯粹的 OI ,源于理论,重在应用。
所以在本篇文章中,我们会更加详细地讲解算法原理,也就是 “源于理论” 。
然后再附加上一些例题以及解题技巧,即:“重在应用” 。
至于时空复杂度的证明等等对于应用没有太大帮助的点,我们仅仅一提就好。
Part 1 SAM 的定义
在了解 SAM 的功能之前,先看看它的定义吧:
- 字符串 \(S\) 的 SAM 是一个可以接受 \(S\) 的所有后缀的最小 DFA (确定性有限状态自动机)。
根据自动机理论,把上面那句话翻译过来就是:
-
SAM 是一张 DAG 。DAG 上的结点被成为 “状态” ,而边被称为状态间的 “转移” 。
-
DAG 存在一个初始结点(状态) \(P\) ,其他所有结点(状态)均可从 \(P\) 出发到达。
-
每个边(转移)被标记上字符集中的一个字母(类似边权),从一个结点出发的所有边(转移)所标记的字母都不同。
-
存在至少一个 “终止结点(状态)” 。如果我们从 \(P\) 出发,通过若干次转移到达了一个终止结点(状态),则路径上的所有边(转移)所标记的字母连接起来所形成的字符串 \(s\) 必定是字符串 \(S\) 的一个后缀。反之,字符串 \(S\) 的每一个后缀均可以表示成 DAG 中一条从 \(P\) 出发到某个终止结点(状态)的路径。
-
在所有满足上述条件的自动机中, SAM 的结点数是最少的(空间最优秀)。
Part 2 SAM 的常用功能
作为一个 DFA ,它可以接受一个字符串所有的后缀。这是显然的,不过它不仅仅是这样。
SAM 最常用的功能是储存一个文本串 \(S\) 的每一个子串,这也是我们在题目主要需要利用的性质。
值得注意的是,对于长度为 \(O(n)\) 的字符串 \(S\), SAM 可以在在 \(O(n)\) 的空间内储存 \(S\) 所有子串的信息,另外,构造 SAM 的算法的时间复杂度仅为 \(O(n)\) 。
总结一下,SAM 最主要的功能之一就是在线性时空内储存一个字符串的所有子串信息。
压缩子串信息
- SAM 包含了字符串 \(S\) 的所有子串。
上面提到过这个性质,原理很简单,既然每个后缀对应了 DAG 上的一条路径,那么考虑沿着某一个后缀 \(s\) 对应的路径走 \(x\) 条边。
设走过的这 \(x\) 条边所标记的字符顺次连接构成了字符串 \(s'\) 。显然如果我们要把 \(s'\) 变成原串的一个后缀 \(s\) ,需要继续沿着这条路径走完剩下的边,并把这条边所标记的字符添加到 \(s'\) 的末尾,直到碰到了这条路径对应的终止结点。
这说明什么?说明 \(s'\) 是 \(s\) 的一个前缀啊!而 SAM 中正好包含了原串的所有后缀,一个字符串的所有后缀的所有前缀显然是这个字符串的所有子串。
栗子
我们来展示一个简单字符串的 SAM ,用蓝色框起初始结点 \(P\) ,终止结点则用红色框起。
譬如字符串 \(S=\text{\{“qwqaqwq”\}}\) ,它的 SAM 应该长成这样子:

比如,我们要给 SAM 一个信号串 "wqaqwq" ,那么它会按照如下路径走:
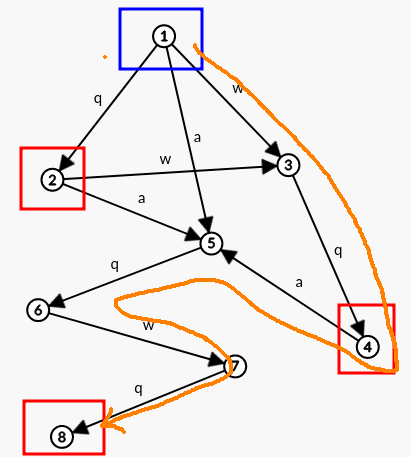
最后走到了终止结点 8 ,这说明 “wqaqwq” 是字符串 "qwqaqwq" 的一个后缀。
如果查询子串呢?比如分别我们查询串 “qaq” 和 “qwq” ,那么它会这样走:
(其中蓝色表示查询 "qaq" ,粉色表示查询 "qwq" 。)
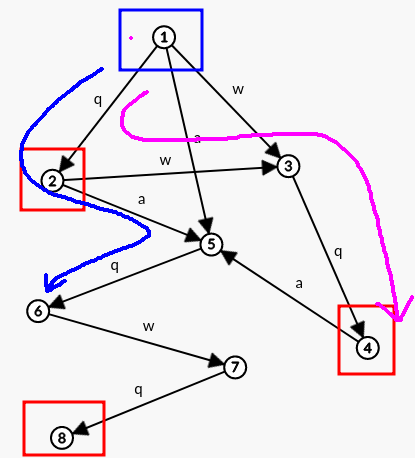
Part 3 后缀树与后缀链接
-
注意此后缀树非彼 “后缀树” !是因为它跳后缀链接访问后缀的性质,导致我喜欢叫它后缀树。实际上,后缀树是一种与 SAM 无关的船新数据结构。
我在翻阅大部分的关于 SAM 的资料中,这棵树被叫做 \(\text{parent}\) 树(以后当着别人面千万别说 SAM 里有后缀树)。
不过我愿意怎么叫就怎么叫,你打我啊?
细心的同学发现了,上面图中可以走出 “qwq” 的路径有两条:\(5\rightarrow 6\rightarrow 7 \rightarrow 8\) 这条路径构成的字符串也是 “qwq” ,究其原因,是因为 “qwq” 在原串中出现了两次。这说明从 \(P\) 开始的遍历并不能保证可以找到所有可以形成 “qwq” 的路径(实际上,根据我们之前的推导,从 \(P\) 出发只能找到 “qwq” 作为某个后缀的前缀出现的情况),也就是会漏掉一些信息。
所以我们需要引进另一种数据结构——后缀树(Suffix Tree),来统计所有本质相同子串的信息。
首先,后缀树是 SAM 的一部分,它是基于 SAM 构建起来的。SAM 中后缀树的 DAG 的关系有点像 ACAM 中 失配树和 Trie 图的关系。
这部分是 SAM 最难理解的部分,如果描述比较劝退的话,可以手画一下图帮助理解,我会尽量多且详细地说明、配图、举例子的。
结束位置 \(\text{endpos}\) 与 \(\text{endpos}\) 等价类
定义与实际意义
考虑字符串 \(S\) 的任意子串 \(s\) ,记 \(\text{endpos}(s)\) 为 \(s\) 在字符串 \(S\) 中每次出现的结束位置(编号从 1 开始),显然 \(\text{endpos}(s)\) 应该是一个非空集合。
譬如字符串 “abab”
S="abab"
s = "a" "b","ab" "aba","ba" "abab","bab"
endpos(s) = {1,3} {2,4} {3} {4}
回到 SAM 的 DAG 上来,我们刚才已经证明过了 “ DAG 中从初始结点 \(P\) 出发,到任意结点 \(x\) 结束的路径都是原串 \(S\) 的一个子串 \(s\) ”,对吧?那么假设走到了任意结点 \(x\) ,那么我们走过的边所标记的字符会构成一个字符串 \(s\) ,\(s\) 是 \(S\) 的一个子串。 此时 \(\text{endpos}(s)\) 可以告诉我们 \(s\) 在哪里出现了,以及出现了几次。譬如我们查询 \(\text{endpos}('ab')=\text{\{2,4\}}\) (实际上,我们一般把这个 \(\text{endpos}\) 的信息记录在结点 \(x\) 里。结点 \(x\) 的 \(\text{endpos}\) 表示从 \(P\) 走到 \(x\) 形成的子串 \(s\) 的 \(\text{endpos}\)),即得到字符 “ab” 出现了两次,结尾分别为 2 和 4 。这样解决了 Part 2 最后提出的 “统计相同子串” 的问题。
另外,显然两个子串 \(s_1,s_2\) 的 \(\text{endpos}\) 可能相等,即 \(\text{endpos}(s_1)=\text{endpos}(s_2)\) ,譬如上面的 “b” 和 “ab” 两个字符串的 \(\text{endpos}\) 都是集合 \(\text{\{2,4\}}\) 。这样,字符串 \(S\) 的所有非空子串 \(s\) 就可以根据它们的 \(\text{endpos}\) 集合被划分为若干等价类。
-
每个等价类 \(E\) 是一个字符串构成的集合,且对于 \(\forall s_1,s_2\in E\) ,有 \(\text{endpos}(s_1)=\text{endpos}(s_2)\) 。
也就是说,同一个等价类中包含的所有字符串的 \(\text{endpos}\) 相同。
在下面,我们用 \(\text{endpos}(E)\) 代表等价类 \(E\) 对应的 \(\text{endpos}\) 集合(请务必区分,等价类是一个字符串集,而 \(\text{endpos}\) 是一个数集)。
举例子之前,先把 SAM 的 DAG 画出来:
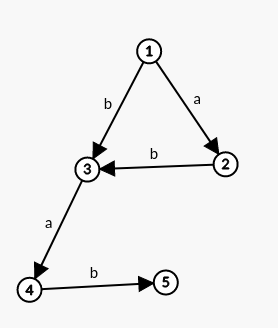
根据上面的对等价类的定义,我们可以得知:“b” 和 “ab” 属于同一个等价类 \(E_x\) 。
把 “b” 和 “ab” 两个子串对应到 DAG 上,发现这两条路径最终都走到了结点 3 。
这说明一个结点同时对应了多个字符串的 \(\text{endpos}\) 值,也就是说,一个结点 \(x\) 对应了一个 \(\text{endpos}\) 等价类 \(E_x\) ,其中包含了若干个 \(\text{endpos}\) 相同的子串(实际上,设从 \(P\) 出发有 \(n\) 条到 \(x\) 的不同路径,则等价类 \(E_x\) 的大小为 \(n\) ,因为每一种路径都表示一个不同的子串)。
相关引理与证明
引理 \(1\) :
考虑两个非空子串 \(s_1,s_2\) ,令 \(|s_1|\geq|s_2|\) 。
\(1.1\) :若 \(s_1,s_2\) 的 \(\text{endpos}\) 相同,那么 \(s_2\) 是 \(s_1\) 的一个后缀,且 \(s_2\) 在 \(S\) 中每一次都以 \(s_1\) 的后缀的形式出现。
\(1.2\) :若 \(s_2\) 是 \(s_1\) 的一个后缀,且 \(s_2\) 在 \(S\) 中每一次都以 \(s_1\) 的后缀的形式出现,那么 \(s_1,s_2\) 的 \(\text{endpos}\) 相同。
证明 \(1.1,1.2\)
-
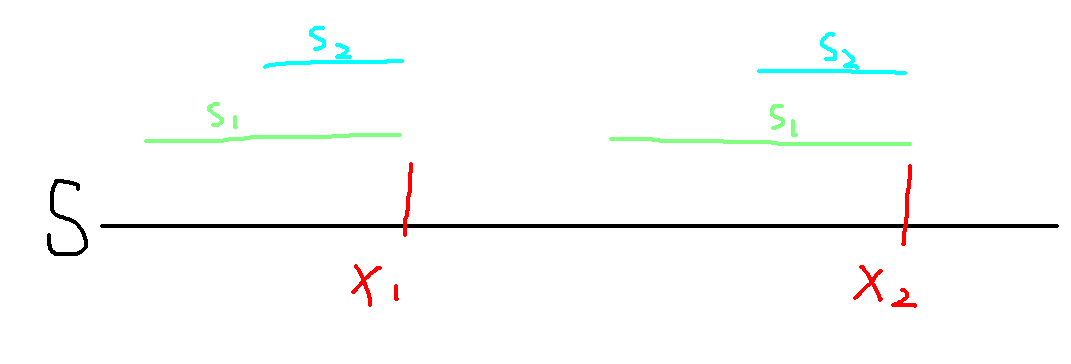
引理显然成立,这个用一张图就可以很直观的说明了:
我们假设 \(\text{endpos}(s_1)=\text{endpos}(s_2)=\{x_1,x_2\}\) ,\(S\) 为原串。
一个简单的事实是:如果 \(s_1\) 在 \(S\) 中出现,那么它的所有后缀 \(s_2\) 一定也会在 \(S\) 中出现。
如果 \(s_2\) 仅仅作为 \(s_1\) 的后缀出现的话,那么每次 \(s_1\) 出现则 \(s_2\) 出现,\(s_1\) 不出现则 \(s_2\) 也不出现,显然它们的 \(\text{endpos}\) 应该相等(如图)。
同理可证明 \(1.2\) (这个比较简单而且好理解,就不再做严谨的证明了)。
Q.E.D
引理 \(2\) :
考虑两个非空子串 \(s_1,s_2\) ,令 \(|s_1|\geq |s_2|\) 。
\(2.1\) :若 \(s_2\) 是 \(s_1\) 的一个后缀,则有 \(\text{endpos}(s_1)\subseteq \text{endpos}(s_2)\) 。
\(2.2\) :若 \(s_2\) 不是 \(s_1\) 的一个后缀,则有 \(\text{endpos}(s_1)\cap \text{endpos}(s_2)=\varnothing\) 。
还是继续利用上面那张图:
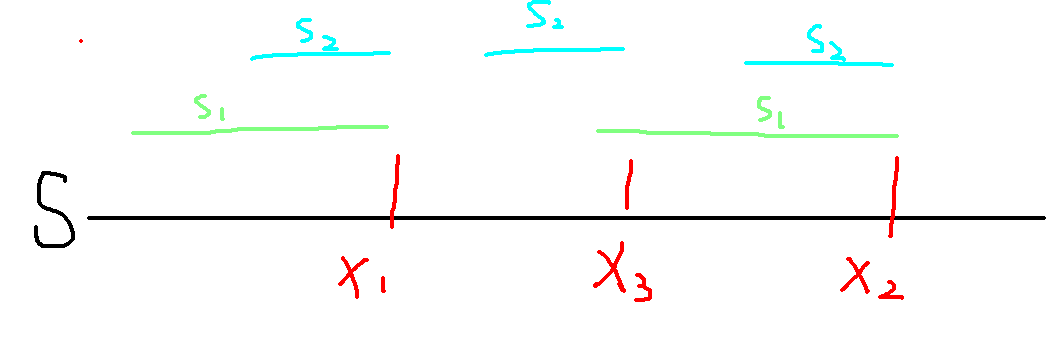
证明 \(2.1\) :
-
设 \(s_2\) 是 \(s_1\) 的一个后缀,那么显然每次 \(s_1\) 出现的时候 \(s_2\) 也必然出现,也就是说 \(\text{endpos}(s_2)\) 至少包含了 \(\text{endpos}(s_1)\) 中的所有元素。
但 \(s_2\) 每次出现的时候 \(s_1\) 却不一定出现(如上图,\(s_2\) 以 \(x_3\) 为结尾出现了一次,但 \(s_1\) 并没有在那里出现)。因此可能会出现一个元素 \(x\) ,使得 \(x\in \text{endpos}(s_2),x\notin \text{endpos}(s_1)\) 。
根据以上两个条件以及集合的定义,推出 \(\text{endpos}(s_1)\subseteq \text{endpos}(s_2)\) 。
特别的,当且仅当不存在这样的 \(x\) 时,有 \(\text{endpos}(s_1)=\text{endpos}(s_2)\),否则 \(\text{endpos}(s_1)\subsetneq \text{endpos}(s_2)\) 。
Q.E.D
证明 \(2.2\) :
-
反证法,设 \(\text{endpos}(s_1)\) 与 \(\text{endpos}(s_2)\) 至少有一个公共元素,且 \(s_2\) 不是 \(s_1\) 的后缀。
我们设这个公共元素为 \(x\) ,那么 \(s_1\) 与 \(s_2\) 在相同位置 \(x\) 结束,观察上图,发现 \(s_2\) 与 \(s_1\) 一定有一方为另一方的后缀。
如果要满足 “ \(s_2\) 不是 \(s_1\) 的后缀” ,那么只能让 \(|s_2|>|s_1|\) ,使得 \(s_1\) 是 \(s_2\) 的后缀,但这与引理中 “令 \(|s_1|\geq |s_2|\) ” 的假设不符。
故 \(\text{endpos}(s_1)\) 与 \(\text{endpos}(s_2)\) 没有公共元素,也即 \(\text{endpos}(s_1)\cap \text{endpos}(s_2)=\varnothing\) 。
Q.E.D
我们约定:记 \(S_l \rightarrow S_r\) 为在 \(S\) 中开头下标为 \(l\) ,结尾下标为 \(r\) 的子串。
基于如上约定,我们来证明引理 \(3\) 的一个结论。
引理 \(3\) :
一个 \(\text{endpos}\) 等价类中不会包括两个本质不同而长度相同的串。

证明:
-
如图,反证法:假设 \(s_1,s_2\) 是同一个等价类 \(E\) 中本质不同的两个子串,且 \(|s_1|=|s_2|=L\) ,原串为 \(S\) 。
那么显然 $s_1=S_{x_1-L+1}\rightarrow S_{x_1} $ ,\(s_2=S_{x_1-L+1}\rightarrow S_{x_1}\) ,发现这两个等式右边是相同的式子,于是推出 \(s_1=s_2\) 。
这个结论对于 \(\text{endpos}(E)\) 中包含的其他的 \(x_2,x_3...x_n\) 也同样适用,不管使用哪个 \(x\) 的值,我们总能得出 \(s_1=s_2\) 的结论。
这与我们假定的 “ \(s_1,s_2\) 是同一等价类 \(E\) 中本质不同的两个子串” 相矛盾,故假设不成立。
综上,引理 3 成立,即一个 \(\text{endpos}\) 等价类中不会包括两个本质不同而长度相同的串。
Q.E.D
我们约定:\(E_i\) 为字符串集合 \(E\) 中包含的第 \(i\) 个字符串(再提醒一下之前提到过的,一个 \(\text{endpos}\) 等价类是一个字符串集合) 。
基于如上约定,我们来证明引理 \(4\) 的两个结论。
引理 \(4\) :
\(4.1\) :考虑一个 \(\text{endpos}\) 等价类 \(E\) ,对于 \(E\) 内任意两个子串,它们要么是相同的串,要么较短者为较长者的真后缀。
\(4.2\) :设 \(l,r\) 分别为 \(E\) 内包含最短和最长子串的长度,则 \(\bigcup |E_i|=\{l\leq x\leq r,x\in N^*\}\) 。
若 \(card(E)=1\) ,两条引理显然成立,不做证明。现在考虑 \(card(E)>1\) 的情况。
证明 \(4.1\) :
- 由引理 \(1.1\) 、引理 \(3\) 结合可得: 在同一个等价类的任意两个不相同子串中,较短者总是较长者的真后缀,引理 \(4.1\) 得证。
Q.E.D
证明 \(4.2\) :
-
分别设一个 \(\text{endpos}\) 等价类 \(E\) 中包含的最长的串为 \(s_1\) ,最短的串为 \(s_2\) 。
一个简单的事实是 \(s_1\) 的所有后缀的长度为集合 \(\{1\leq x\leq |s_1|,x\in N^* \}\) (不考虑空串)。那么一定存在一个字符串集合 \(Q\) ,使得 \(Q\) 中每个字符串都是 \(s_1\) 的后缀(不考虑空串)并且满足 \(\bigcup |Q_i|=\{|s_2|\leq x \leq |s_1|,x\in N^*\}\) 。
我们发现, \(Q\) 集合的范围就是需要证明的 \(E\) 的范围,于是只要证明 \(E=Q\) 。
根据高中数学的知识,如果要证明两集合 \(E=Q\),要分别证明 \(E\subseteq Q,Q\subseteq E\) 。
-
由引理 \(4.1\) ,我们可以得出 \(E\) 中所有的串都是最长串 \(s_1\) 的后缀,而根据我们做出的定义, \(Q\) 中所有的串也都是 \(s_1\) 的后缀。
我们又知道 \(E\) 中最长的串长度为 \(|s_1|\) ,最短的为 \(|s_2|\) ,而 \(Q\) 中包含了 \(s_1\) 的每一个长度在 \(|s_2|\) 到 \(|s_1|\) 之间的后缀,由此得出 \(E\subseteq Q\) 。
-
设 \(s_i\) 是 \(Q\) 中非 \(s_1,s_2\) 的一个串,显然 \(s_2\) 应该是 \(s_i\) 的真后缀,\(s_i\) 是 \(s_1\) 的真后缀 。
反证法,我们已经知道 \(s_1,s_2\in E,s_1,s_2\in Q\) ,如果命题的第二部分不成立,那么只要证明: \(\exists \ s_i\notin E\) 。
如果存在这样一个 \(s_i\notin E\) ,设 \(s_i\in E'\) ,分别对 \(s_2,s_i\) 、\(s_i,s_1\) 使用引理 \(2.1\) ,得出 \(E\subseteq E'\subseteq E\) 。
根据集合的定义,\(E'=E\) ,即 \(\forall s_i\in E\) 。这与我们假设的 \(\exist \ s_i\notin E\) 不符,故原命题成立,即 \(Q\subseteq E\) 。
综上所述,有 \(E=Q\) ,故 \(E\) 与 \(Q\) 的范围相同,引理 \(4.2\) 得证。
-
Q.E.D
后缀链接 \(\text{link}\) 与后缀树
定义与实际意义
考虑 SAM 中某个不是初始结点的结点 \(v\) 。上面已经说过,每个结点代表一个等价类,定义 \(w\) 为这个等价类所包含的字符串中最长的一个。
我们记串 \(t\) 为最长的、与 \(w\) 不属于统一等价类的、\(w\) 的一个真后缀,把 \(v\) 的后缀链接连到 \(t\) 所属的等价类 \(u\) 上(根据定义,\(u\) 也是一个结点)。
根据引理 \(4.2\) ,我们从某个等价类 \(E\) 不断跳 \(\text{link}\) 到初始结点 \(P\) 就可以访问 \(E\) 中最长子串 \(w\) 的每一个后缀,这就是后缀链接的实际意义。
相关引理与证明
引理 \(5\) :
设一个 \(\text{endpos}\) 等价类为 \(E\) ,\(E\) 中最短的串为 \(s\) 。
\(5.1\) :\(\text{link}(E)\) 中最长的串是 \(s\) 的长度为 \(|s|-1\) 的真后缀。
\(5.2\) :\(E\subsetneq \text{link}(E)\)
证明 \(5.1\) :
-
根据定义以及引理 \(4.2\) ,我们可以推出引理 \(5.1\) 。
这很简单,不过这个结论不是我们想要的,我们对其做一步转化——
\(E\) 中最短的串 \(\text{short}\) 的长度可以表示为 \(\text{link}(E)\) 中最长的串 \(\text{long}\) 的长度 +1 。
转化的正确性也显然,不过它告诉我们一个重要的信息:我们可以通过 “最长” 求 “最短” 。
利用这个引理,后缀自动机的结点 \(v\) 中便只要记录等价类 \(v\) 包含的最长的子串的长度了。
Q.E.D
证明 \(5.2\) :
-
下面是引理 \(2.1\) (一个显然的条件是 \(\text{link}(E)\) 中的字符串都是 \(E\) 中的字符串的真后缀,这也是我们运用引理 \(2.1\) 的基础):
\(2.1\) :若 \(s_2\) 是 \(s_1\) 的一个后缀,则有 \(\text{endpos}(s_1)\subseteq \text{endpos}(s_2)\) 。
显然这里单个字符串 \(s_1,s_2\) 可以用它所对应的 \(\text{endpos}\) 等价类 \(E\) 与 \(\text{link}(E)\) 替换掉。
把引理 \(2.1\) 用等价类 \(E\) 和 \(\text{link}(E)\) 替换掉之后,我们要做的就是证明 \(E\neq \text{link}(E)\) ,而这就是 \(\text{link}\) 的定义之一。
Q.E.D
引理 \(6\) :
所有后缀链接构成一棵以 \(P\) 为根的内向树(后缀树)。
下面的证明应该是没什么用,实际上,你只需要知道它是一棵树就足够了。
在题目中,我们一般是拿这棵树去做一些树形 DP 来统计子串信息。
证明 \(6\) :
-
根据后缀链接的定义,我们从任意结点 \(A\) 沿着后缀链接访问,总能访问到结点 \(P\) ,于是可以得知 “后缀图” 联通。
现在只要证明后缀图从任意结点 \(A\) 出发,到 \(P\) 的路径有且只有一条,就可以证明它是一棵内向树。
考虑 \(A\rightarrow P\) 有多条路径存在的情况,大致如下:
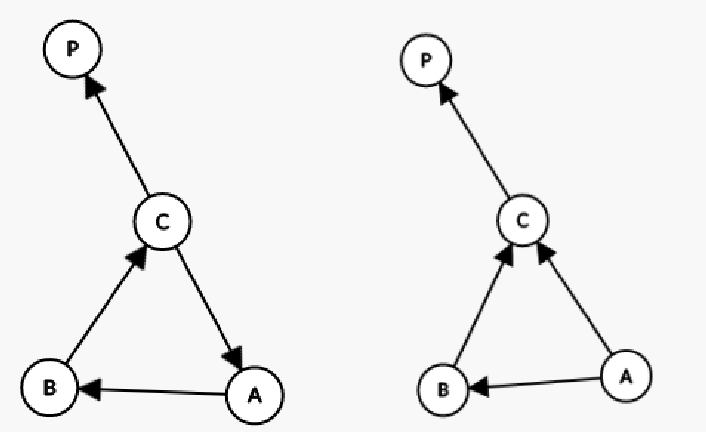
先来证明左边的情况:
- 若出现这种情况,根据引理 \(5.2\) ,可以得出一个非常 naive 的结论—— \(A\subsetneq B\subsetneq C \subsetneq A\) ,而这是绝对不可能的。
再来证明右边的情况:
-
继续运用引理 \(5.2\) ,得出 \(A\subsetneq B \subsetneq C,A\subsetneq C\) ,这在数学上暂时还是说得过去的。
我们还知道 \(w\) 的前几个后缀(按照长度降序考虑)可能和 \(w\) 属于同一个等价类,且其他的后缀(至少一个——空串)一定属于其他的等价类。
我们记串 \(t\) 为最长的 “其他的后缀” ,把 \(v\) 的后缀链接 \(\text{link}\) 连到 \(t\) 所属的 \(\text{endpos}\) 等价类 \(u\) 上(根据定义,\(u\) 应该也是 DAG 上的一个结点)。
上面是后缀链接的定义,显然 \(w\) 的后缀链接只能连接到 “最长的其他的后缀串 \(t\) ” 所属的等价类 \(u\) 上,也就是说,一个点只能有一条后缀链接。
在上图中,\(A\) 拥有两条后缀链接,这显然是不可能的。
另外,\(P\) 对应空串,所以 \(P\) 不可能有后缀链接。
故原命题得证,即:所有后缀链接构成一棵以 \(P\) 为根的内向树。
Q.E.D
栗子
理论的东西终于差不多了,把这棵后缀树和 DAG 结合起来,SAM 就诞生了。
下面改一改 OI Wiki 上的两张图,我们具体看看后缀树长成什么样(以字符串 “abcbc” 为例)。
后缀树不是建立在 DAG 上的,而是与 DAG 公用结点,二者的边都是独有的,如下图。
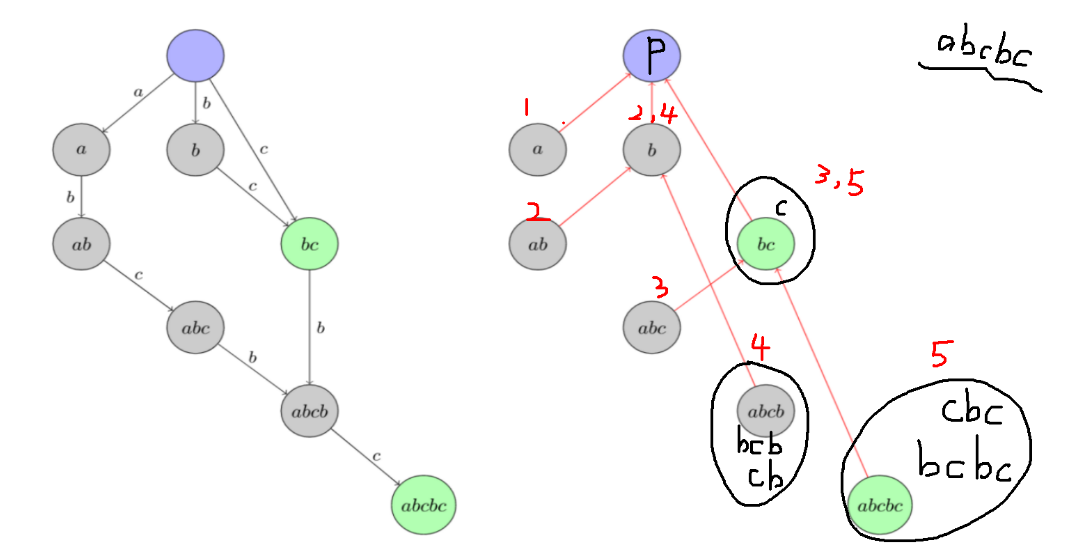
原图只写出了每个等价类(结点)内最长的字符串是谁,这里用黑笔把每个等价类内其他的字符串补充出来了。
每个等价类(结点)上用红笔标记的是这个等价类对应的 \(\text{endpos}\) 具体包含了哪些元素(譬如串 “bc” 的 \(\text{endpos}\) 是 \(\text{\{3,5\}}\) ,就在结点上写了 3,5 )。
读者可以结合这两张图验证、加深理解一下之前证明过的引理。
小结
看了这么多引理,是不是该总结一下呢?
在下面会引入一些辅助记号,作为介绍构造 SAM 算法的基础。
-
原串 \(S\) 的每一个子串可以根据它们的 \(\text{endpos}\) 被划分为多个等价类,而每个等价类又对应了 DAG 以及后缀树上的一个结点(\(\text{endpos}\) 的定义一节中提到)。
-
对于每一个结点 \(v\) ,它对应一个等价类 \(E\) 。我们记 \(\text{long}(v)\) 为 \(E\) 中最长的串,\(\text{len}(v)\) 为其长度;\(\text{short}(v)\) 为 \(E\) 中最短的串,\(\text{minlen}(v)\) 为其长度。那么 \(E\) 中每个串都是 \(\text{long}(v)\) 的后缀,且所有字符串的长度的并集为 \(\{\text{minlen}(v)\leq x\leq \text{len}(v),x\in N^*\}\)(引理 \(2.1,3,4.2\) ,即不重不漏覆盖整数区间)。
-
从任意结点 \(v_0\) 顺着后缀链接遍历,总可以访问到 \(P\) 。途中会访问到若干结点 \(v_i\) , \(v_i\) 中包含的字符串的长度恰好覆盖一段区间 \([\text{minlen}(v_i),\text{len}(v_i)]\) 的每一个整数,并且每一个 \(v_i\) 恰好覆盖的区间都不相交,这些区间的并为 \(\{0\leq x\leq \text{len}(v_0),x\in N^*\}\) (连续运用引理 \(3,4.2\))。
-
对于非 \(P\) 的一个结点 \(v\) ,可以用后缀链接的形式表达 \(\text{minlen}(v)\) ,即:\(\text{minlen}(v)=\text{len}(\text{link}(v))+1\) 。所以,我们在后缀自动机中,对于每个结点 \(v_i\) 通常只记录 \(\text{len}(v_i)\)(引理 \(5.1\))。
-
设一个 \(\text{endpos}\) 等价类为 \(E\) ,\(E\) 中最短的串为 \(s\) ,则 \(\text{link}(E)\) 指向 \(s\) 的长度为 \(|s|-1\) 的真后缀所属的等价类 \(E'\) (后缀链接定义)。所有的后缀链接形成一棵以 \(P\) 为根的内向树(引理 \(6\))。后缀链接同时也可以表示 \(\text{endpos}\) 等价类之间的包含(子集)关系(引理 \(5.2\))。
Part 4 构造算法
讲了这么多理论,终于该动手构造 SAM 了。
构造 SAM 的算法是一个在线算法,在这个算法中,我们依次把字符加入 SAM ,并在每一步中动态维护它。
这个过程可能有些难以理解,所以下面会先展示算法流程,稍后再逐步说明原理,最后给出代码实现。
算法流程
一开始,SAM 中只有一个结点 \(P\) ,编号为 0 (其他结点编号 1、2 ... )。为了方便,我们钦定 \(\text{len}(P)=0,\text{link}(P)=-1\)( -1 表示虚拟状态)。
现在我们的任务是实现给当前 SAM 添加一个字符 \(c\) 的过程,算法流程如下:
-
令 \(last\) 为添加 \(c\) 之前整个字符串 \(S\) 所对应的结点(从 \(P\) 出发走到 \(last\) 的路径上边组成的串是 \(S\) ,一开始设 \(last=0\) ,算法的最后一步更新它)。
-
创建一个新的状态 \(cur\) ,并将 \(\text{len}(cur)\) 赋值为 \(\text{len}(last)+1\) 。
-
从 \(last\) 开始遍历后缀链接,如果当前结点 \(v\) 没有标记字符 \(c\) 的出边,创建一条 \(v\rightarrow cur\) 的边,标记为 \(c\) 。
-
如果遍历到了 \(P\) ,赋值 \(\text{link}(cur)=0\) ,转 8 。
-
如果当前结点 \(v\) 已经有了标记字符 \(c\) 的出边,停止遍历,并把这个结点标记为 \(p\) ,标记 \(p\) 沿着标记字符 \(c\) 的出边到达的点为 \(q\) 。
-
如果 \(\text{len}(p)+1=\text{len}(q)\) ,赋值 \(\text{link}(cur)=q\) ,转 8 。
-
否则情况会很复杂。
复制状态 \(q\) 到一个新的状态 \(copy\) 里(包括 \(\text{link}(q)\) 以及所有 \(q\) 在 DAG 上的出边),将 \(\text{len}(copy)\) 赋值为 \(\text{len}(p)+1\) 。
复制之后,再赋值 \(\text{link}(q)=copy,\text{link}(cur)=copy\) 。
然后从 \(p\) 遍历后缀链接,设当前遍历到的点为 \(v\) ,若 \(v\) 有标记为 \(c\) 的出边 \(v\rightarrow q\) ,则重定向这条边为 \(v\rightarrow copy\) 。
若 \(v\) 没有标记为 \(c\) 的出边或者 \(v\) 的标记为 \(c\) 的出边所到达的点不是 \(q\) ,停止遍历,转 8 。
-
把 \(last\) 赋值为 \(cur\) ,转 1 。
算法原理
我们将按照算法的八个步骤依次说明。
-
找到 \(last\) ,为之后的更新做准备。
-
加入 \(c\) 之后,串就变成了 \(S+c\) ,这一步操作后显然会出现一些新的等价类( \(\text{endpos}\) 包含新来的字符 \(c\) 的位置)我们创建这个新的等价类为 \(cur\) 。
根据我们上面对 \(last\) 的定义,显然 \(last\) 中最长的字符串就是 \(S\) ,长度为 \(\text{len}(last)\) 。
因为新串是 \(S+c\) ,应该从 \(S\) 添加一条到 \(cur\) 的边,标记为 \(c\) ,表示可以从 \(S\) 转移到 \(S+c\) 。
等价类 \(cur\) 中包含的最长的字符串应该是 \(S+c\) ,故赋值 \(\text{len}(cur)=\text{len}(last)+1\) 。
-
遍历后缀链接,尝试添加到 \(cur\) 的转移。
SAM 做的工作是记录串的每一个后缀。现在新串是 \(S+c\) ,那么我们只要在原来记录的每一个后缀的后面添加一个 \(c\) 就可以了。
根据引理 \(4.2\) 以及 \(\text{link}\) 的定义,从 \(last\) 开始遍历 \(\text{link}\) 可以访问原串 \(S\) 的所有后缀,我们依次尝试在这些等价类之后添加连向 \(cur\),标记为 \(c\) 的边。
如下图,这是一个向 SAM 中添加字符 “d” 的过程,红色表示跳的后缀链接,黑笔标记的边为新建边。
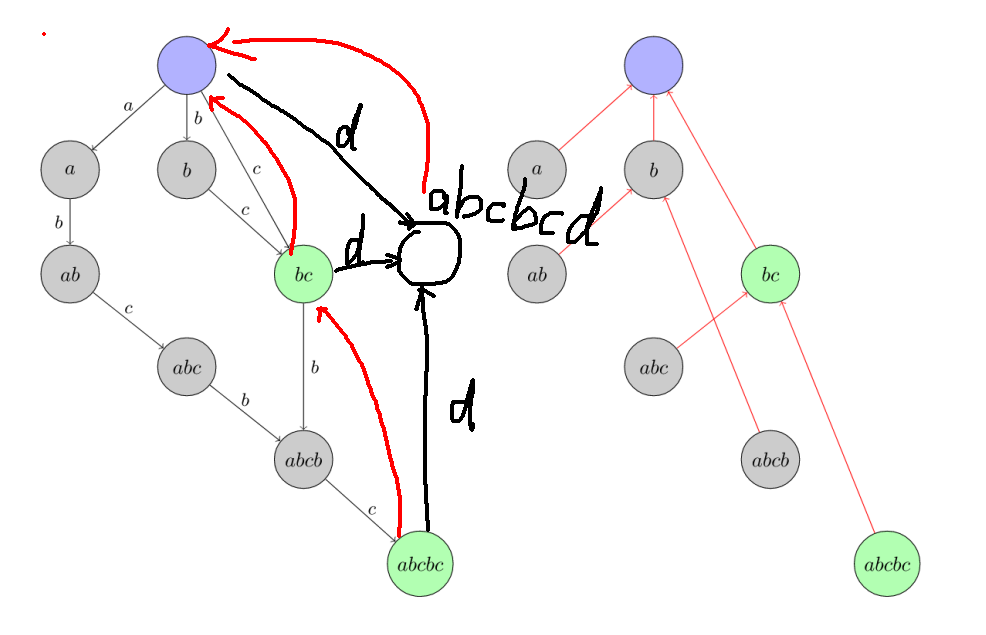
引理 \(7\) :特别地,当且仅当跳后缀连接一直跳到了 \(P\) 结点,说明加入的字符 \(c\) 在之前的串 \(S\) 中没有出现过。
证明 \(7\) :
-
还记得 SAM 是如何存下字符串的所有子串信息的吗?——沿着某一个后缀走 \(x\) 条边对应的字符串是一个原串的子串。
我们现在遍历了原串的每一个后缀,从这些后缀出发,我们找不到任何一条标记为 \(c\) 的边。
也就是说,不存在任何一个后缀的前缀是单个字符 \(c\) ,由此得出 \(c\) 在 \(S\) 中没有出现过。
Q.E.D
-
上面已经证明过,如果要执行 \(4\) ,说明这次添加的字符 \(c\) 在之前没有出现过。
这也就说明,\(S\) 中不存在新串 \(S+c\) 的任何一个非空后缀,根据 \(\text{link}\) 的定义,应该把 \(cur\) 的 \(\text{link}\) 连向空串。
-
一个辅助性的步骤,不做过多说明。
-
步骤 \(6,7\) 本质上是在处理相同问题( \(cur\) 的后缀链接问题)的不同情况,我们放在一起讨论。
首先,根据小结中的第 \(3,4\) 条 ,明确一点:从 \(last\) 开始跳后缀链接,每一次访问到的某个等价类 \(p\) 中,\(p\) 包含的所有字符串都是原串 \(S\) 的后缀。并且 \(\text{long}(p)\) 的长度 \(\text{len}(p)\) 单调递减,这样我们推出 \(\text{long}(p)+c\) 的长度 \(\text{len}(p)+1\) 也单调递减,我们在后面的证明中会用到这一点。
我们从 \(last\) 向 \(P\) 跳后缀链接,设第一次遇到的拥有一条 \(c\) 的出边的结点为 \(p\) ,从 \(p\) 经 \(c\) 的出边到达了 \(q\) 。
根据定义,\(p\) 中包含串 \(\text{long}(p)\) ,而 \(\text{long}(p)\) 再沿着这条 \(c\) 的出边走就形成了串 \(\text{long}(p)+c\) ,换句话说——我们找到了串 \(\text{long}(p)+c\) 。
那么这有什么用呢? \(\text{long}(p)\) 是原串 \(S\) 的后缀,故 \(\text{long}(p)+c\) 是新串 \(S+c\) 的后缀。又因为 \(\text{long}(p)+c\) 长度的单调递减性质,我们找到的第一个串 \(\text{long}(p)+c\) 对于 \(\text{long}(cur)\) 来说,不就是 “最长的、不与 \(\text{long}(cur)\) 属于同一等价类的、\(\text{long}(cur)\) 的后缀” 吗?这正是后缀链接的定义,于是 \(\text{long}(p)+c\) 就应该是 \(\text{link}(cur)\) 中最长的字符串。
现在问题来了:\(\text{link}(cur)\) 应该连向一个所包含最长串是 \(\text{long}(p)+c\) 的结点,而 \(q\) 包含了串 \(\text{long}(p)+c\) ,但 \(\text{long}(p)+c\) 是不是 \(q\) 中的最长字符串还不知道。
-
如果 \(\text{len}(q)=\text{len}(p)+1\) ,根据引理 \(3\) ,我们推断出 \(q\) 中最长的字符串一定是 \(\text{long}(p)+c\) ,这时直接赋值 \(\text{link}(cur)=q\) 。
-
如果 \(\text{len}(q)\neq \text{len}(p)+1\) ,这说明 \(q\) 中最长的字符串不是 \(\text{long}(p)+c\) ,那么我们就不能直接赋值。
既然我们需要一个包含最长字符串为 \(\text{long}(p)+c\) 的等价类,那么我们可以把 \(\text{long}(p)+c\) 及其在 \(q\) 中的所有后缀从 \(q\) 中拿出来,让它们单独构成一个新的等价类 \(copy\) 。这时这个新的等价类 \(copy\) 就满足了 \(\text{link}(cur)\) 的要求,赋值 \(\text{link}(cur)=copy\) 。
现在考虑分裂 \(q\) 造成的影响:
-
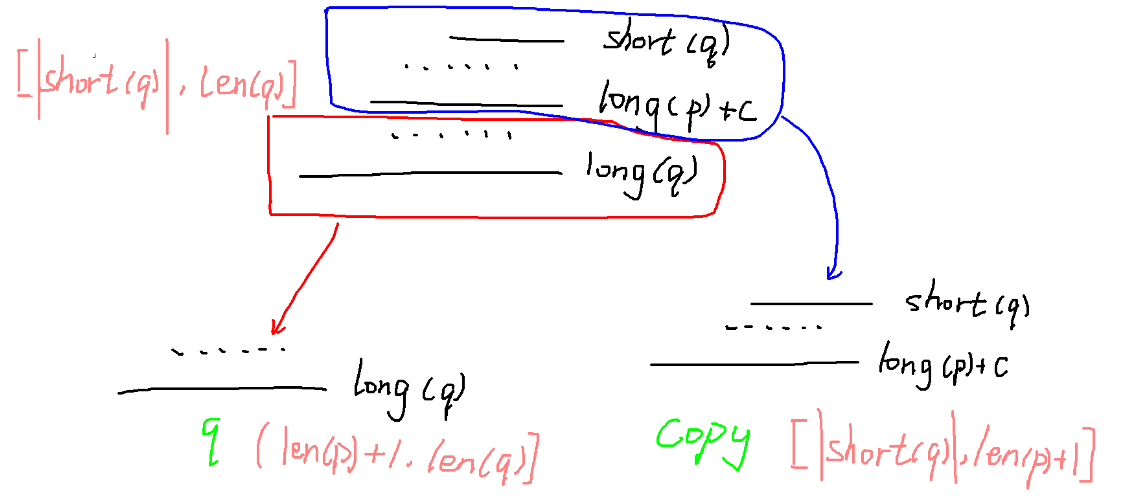
下面的 \(q\) 均指被拆分之前的等价类 \(q\),如有特殊需要,会使用 “新等价类 \(q\)” 加以区分。
如上图,我们实际上是从一个包含的字符串的长度可以覆盖区间 \([|\text{short}(q)|,\text{len}(q)]\) 中每一个整数的等价类 \(q\) 中拆分出一个包含的字符串的长度可以覆盖区间 \([|\text{short}(q)|,\text{len}(p)+1]\) 中每一个整数的等价类 \(copy\) 。顺便可以得出新等价类 \(q\)中包含的字符串的长度恰好覆盖区间 \((\text{len}(p)+1,\text{len}(q)]\) 中每一个整数。
考虑 \(copy\) 的 \(\text{link}\) 该连向谁。\(\text{link}(q)\) 是 \(q\) 中所有字符串的后缀,也就必然是 \(\text{long}(copy)\) 的后缀。据引理 \(5.1\) 推出 \(\text{len}(\text{link}(q))=|\text{short}(q)|-1\) 。再对 \(copy\) 用一遍引理 \(5.1\) ,发现 \(\text{len}(\text{link}(copy))=|\text{short}(q)|-1\) 。也就是说,\(\text{link}(q)\) 恰好满足了成为 \(\text{link}(copy)\) 的条件,于是 \(\text{link}(copy)=\text{link}(q)\) 。
据图,\(copy\) 中的字符串都是新等价类 \(q\)中字符串的后缀。而 \(\text{len}(\text{link}(q))=|\text{short}(q)|-1<\text{len}(p)+1\) , 这说明 \(\text{long}(copy)\) 才是 “\(\text{long}(q)\) 的最长的、不与 \(\text{long}(q)\) 属于同一等价类的、\(\text{long}(q)\) 的后缀”,也就是 \(\text{link}(q)=copy\) 。
考虑新等价类在 DAG 上的出边如何分配。因为 \(copy\) 是从 \(q\) 中分裂出来的,\(copy\) 中的串在分裂之前与新等价类 \(q\) 中的串共用 \(q\) 的出边,即使现在这些串被分出去了,它们也应该拥有之前的出边。于是应该把 \(q\) 的所有出边复制给 \(copy\) 。
除此之外,我们还要重定向一些出边。
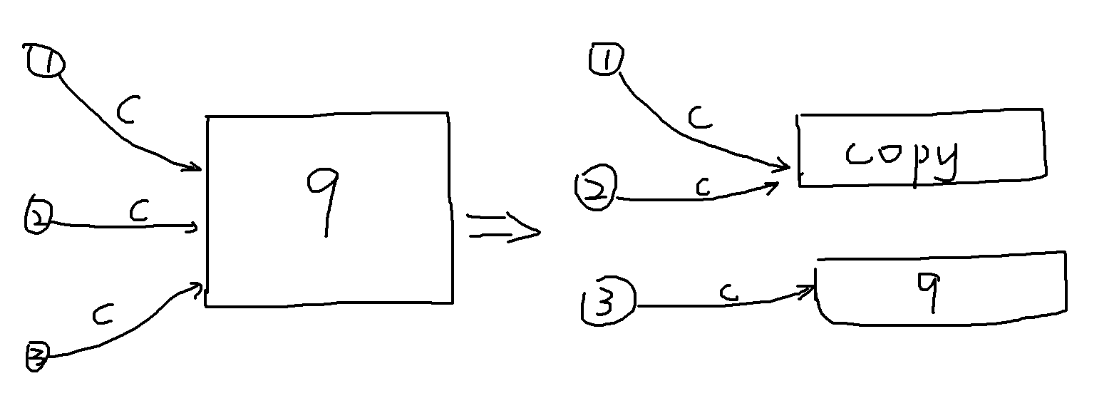
如上图,相信重定向边的原因大家看图也能看个八九不离十吧。
原来的 \(q\) 有若干条入边,每一条都构成了 \(q\) 中包含的一个字符串。但是现在 \(q\) 分家了,我们就必须要区分清楚,到底是哪些入边构成了被分出去的串,哪些构成了还剩下在 \(q\) 中的串(如果不做修改,那么我们的程序默认所有边都指向了新等价类 \(q\) ,这样显然不对)。
那么具体是哪些出边呢?显然只有 \(\text{long}(p)\) 的某个后缀加上 \(c\) 才可以构成 \(copy\) 中的某个串(\(copy\) 中的串都是 \(\text{long}(p)+c\) 的后缀)。那么从 \(p\) 继续向 \(P\) 遍历后缀链接——
- 如果找到了一个结点 \(v\) 拥有一条标记 \(c\) 的出边指向 \(q\) ,说明 \(v\) 中的串加上 \(c\) 构成了 \(copy\) 中的串,我们要把这条边重定向到 \(copy\) 。
- 如果找到了一个结点 \(v\) 拥有一条标记 \(c\) 的出边,但指向结点不是 \(q\) ,说明 \(v\) 中的串加上 \(c\) 构成了一个不在 \(copy\) 集合中的 \(\text{long}(copy)\) 的后缀(\(copy\) 在后缀树上的某一级祖先中的一个串)。因为 \(v\) 中的串加上 \(c\) 无法构成 \(copy\) 中的串,那么 \(v\) 的后缀加上 \(c\) 显然也无法构成 \(copy\) 中的一个串。也就是说,我们已经把所有要重定向的边完成重定向了,停止遍历即可。
-
最后一步,把 \(last\) 设置为 \(cur\) ,表示要把本次加进来的新串作为原串 \(S\) ,以备加入下一个字符的需要。
-
实际上,关于分裂操作的原因,还有另一种证明方法(使用 \(\text{endpos}\) 等价类在被更新时的兼容性来说明),不过如果要再说明一遍,篇幅未免有点长了。如果读者对它感兴趣的话,我就在这里给大家起个头吧:
如果我们要加入 \(c\) ,此时 \(\text{long}(p)+c\) 及其所有后缀应该作为 \(S+c\) 的后缀出现一次,这些字符串的 \(\text{endpos}\) 集合内应该被添加一个新的元素—— \(|S|+1\) 。但是如果 \(\text{len}(q)\neq \text{len}(p)+1\) ,也就是说,\(q\) 中包含的字符串除了 \(\text{long}(p)+c\) 还有一些更长的串 \(x\) 。\(x\) 并没有作为 \(S+c\) 的后缀出现,故 \(x\) 的 \(\text{endpos}\) 内不应该被添加 \(|S|+1\) 这个元素。此时一个等价类 \(q\) 内出现了两类 \(\text{endpos}\) 不相同的字符串,这不符合等价类的定义,故 \(q\) 注定分裂。
……
下面将用图展示 SAM 的构造过程(以串 “abcbc” 为例):
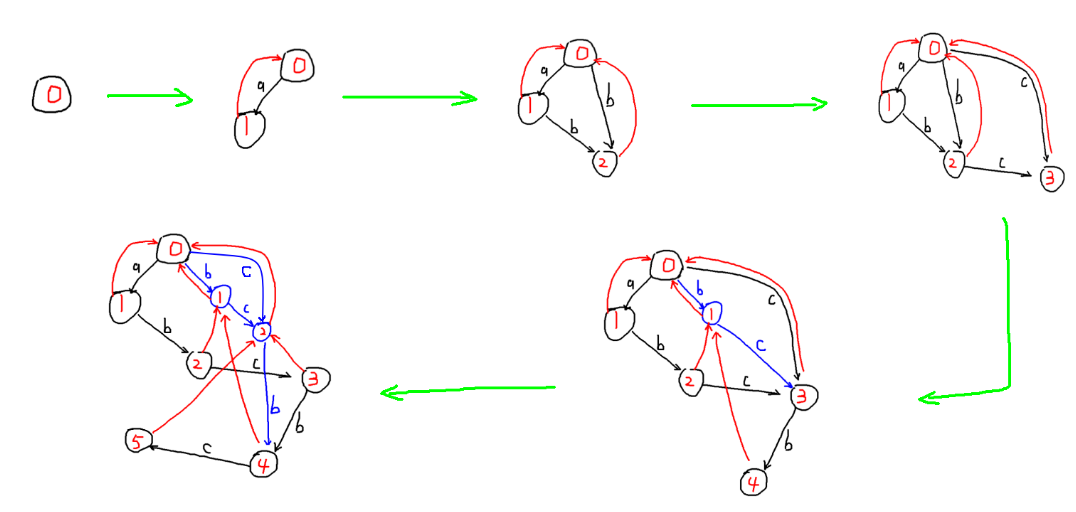
食用指南:
- 黑色点表示 DAG 中的结点,黑色边表示 DAG 中的出边,边上标记了字母。
- 蓝色点表示这个点是分裂得到的,蓝色边表示这条边是复制过来的或者重定向过的。
- 红色边表示后缀树上的边。
- 每个点内的数字表示这个点包含的最长字符串的长度( \(P\) 到该结点的最长路长度)。
我们来模拟一下这个后缀自动机的建立过程吧:
- 初始时,只有一个结点 \(P\) ,表示初始结点。
- 添加 “a” ,满足构造算法的第 \(4\) 步,后缀链接到 \(0\) 。
- 添加 “b” ,满足构造算法的第 \(4\) 步,后缀链接到 \(0\) 。
- 添加 “c” ,满足构造算法的第 \(4\) 步,后缀链接到 \(0\) 。
- 添加 “b” ,跳后缀链接到 \(P\) ,发现 \(P\) 有标记 “b” 的出边,到达的结点 \(q\) 的最长串长度是 2 ,分裂 \(q\) ,重定向边。
- 添加 “c” ,跳后缀链接到 \(5\) 中分裂出来的点,发现该点有标记 “c” 的出边,到达的结点 \(q\) 的最长串长度是 3 ,分裂 \(q\) ,重定向边。
这样,你就得到了和 OI Wiki 上给出的一模一样的后缀自动机啦,好耶!
复杂度与其他必要信息
时空复杂度
上面我们提到过,SAM 的复杂度是线性的,这是建立在字符集大小 \(|\sum|\) 为常数的情况下,如果 \(|\sum|\) 不是常数,那么 SAM 的复杂度就不是线性的。
如果字符集过大,那么我们需要在每个结点维护一个 map 存下从该点出发经过字符 \(x\) 所到达的结点编号(利用 map 建立 char 到 int 的映射)。因此,如果不能忽略字符集大小的话,算法的渐进复杂度应为 \(O(n\log |\sum|)\) ,空间复杂度 \(O(n)\) 。
如果字符集足够小(例如 26 个英文字母),可以不用写 map ,用空间换时间在每个结点存为一个大小为 \(|\sum|\) 的 int 数组,直接存该边到达结点编号。这样算法的时间复杂度为 \(O(n)\) ,空间复杂度升至 \(O(n|\sum|)\) 。
结点数
对于一个长度为 \(n\) 的字符串,它的 SAM 中的结点数不会超过 \(2n-1\)(假设 \(n\geq 2\))。
这是一个必要的结论,它可以告诉我们写 SAM 的时候代表结点的数组大小要开 2 倍。
具体地,字符串 “abbb...bbb” 可以使得这个值达到上限 \(2n-1\) 。
边数
对于一个长度为 \(n\) 的字符串,它的 SAM 中的边数不会超过 \(3n-4\)(假设 \(n\geq 3\))。
如果使用 map 实现 SAM ,那么这条结论可以让我们预估 SAM 的空间复杂度。
具体地,字符串 “abbb...bbbc” 可以使得这个值达到上限 \(3n-4\) 。
代码实现
下面给出三种实现的方式,一种是直接使用数组实现,一种则封装在了结构体内。另外,笔者再给出一种使用 map 的实现方式。
PS:对于一些毒瘤题目,我们可能需要写两个或者更多后缀自动机,这时使用封装在结构体内的实现方式比较方便。
/*---------- 结构体封装版本 ----------*/
struct Suffix_Automaton{
int len[maxn<<1],link[maxn<<1];//和说明中提到的意义相同
int ch[maxn<<1][26];//每个结点开字符集大小的数组
int siz,last;//siz 用来新建结点,last 同说明中的意义
std::vector<int>v[maxn<<1];
inline void init(){
memset(len,0,sizeof len);
memset(link,0,sizeof link);
memset(ch,0,sizeof ch);
memset(mx,0,sizeof mx);
for(int i=0;i<200000;++i) v[i].clear();
siz=last=0;//初始化不能忘
link[0]=-1;//这一句很重要,我们要初始化 link(0) 为虚拟结点
}
inline void extend(const char *str){//在当前变量中建立 str 的 sam
int n=std::strlen(str);
for(int _=0;_<n;++_){
int cur=++siz,p=last,c=str[_]-'a';//意义同证明中提到的
len[cur]=len[p]+1;//初始化新结点的 len
while(p!=-1 && !ch[p][c]){//跳 link 尝试添加边
ch[p][c]=cur;
p=link[p];
}
if(p==-1) link[cur]=0;//直接跳到了 0 (初始结点),赋值 link(cur)=0
else{
int q=ch[p][c];//找到了 q 为 p 的 c 出边
if(len[q]==len[p]+1) link[cur]=q;//len(q)=len(p)+1 的情况
else{//分裂结点的情况
int copy=++siz;
len[copy]=len[p]+1;
link[copy]=link[q];
for(int i=0;i<26;++i) ch[copy][i]=ch[q][i];//初始化分裂的结点 copy
while(p!=-1 && ch[p][c]==q){
ch[p][c]=copy;
p=link[p];//重定向路径
}
link[q]=link[cur]=copy;//修改 q 和 cur 的 link 为 copy
}
}
last=cur;//最后一步更新 last
}
for(int i=1;i<=siz;++i) v[link[i]].push_back(i);//建立后缀树
}
}sam;
/*---------- 不封装版本 ----------*/
struct Suffix_Automaton{
int link,len;
int ch[26];
}SAM[maxn<<1];
int siz,last;
std::vector<int>Suffix_Tree[maxn<<1];
void SAM_extend(const int c){
int cur=++siz,p=last;
SAM[cur].len=SAM[p].len+1;
while(p!=-1 && !SAM[p].ch[c]){
SAM[p].ch[c]=cur;
p=SAM[p].link;
}
if(p==-1) SAM[cur].link=0;
else{
int q=SAM[p].ch[c];
if(SAM[q].len==SAM[p].len+1) SAM[cur].link=q;
else{
int copy=++siz;
SAM[copy].len=SAM[p].len+1;
SAM[copy].link=SAM[q].link;
for(int i=0;i<26;++i) SAM[copy].ch[i]=SAM[q].ch[i];
while(p!=-1 && SAM[p].ch[c]==q){
SAM[p].ch[c]=copy;
p=SAM[p].link;
}
SAM[q].link=SAM[cur].link=copy;
}
}
last=cur;
}
//在主函数中
link[0]=-1;
int lenth=strlen(str);
for(int i=0;i<lenth;++i) SAM_extend(str[i]-'a');
/*---------- map 版本 ----------*/
struct Suffix_Automaton{
int len,link;
std::map<int,int>ch;
}SAM[maxn<<1];
int siz,last;
void SAM_extend(int c){
int cur=++siz,p=last;
SAM[cur].len=SAM[last].len+1;
while(p!=-1 && !SAM[p].ch.count(c)){
SAM[p].ch[c]=cur;
p=SAM[p].link;
}
if(p==-1) SAM[cur].link=0;
else{
int q=SAM[p].ch[c];
if(SAM[q].len==SAM[p].len+1) SAM[cur].link=q;
else{
int copy=++siz;
SAM[copy].len=SAM[p].len+1;
SAM[copy].link=SAM[q].link;
SAM[copy].ch=SAM[q].ch;
while(p!=-1 && SAM[p].ch.count(c)){
if(SAM[p].ch[c]==q) SAM[p].ch[c]=copy,p=SAM[p].link;
else break;
}
SAM[q].link=SAM[cur].link=copy;
}
}
last=cur;
}
更多性质
下面的内容基于读者已经对前面的引理以及后缀树有一个比较全面的认识和了解(其实是懒得写证明了)。
分配结束标记
说了这么多,后缀自动机的初心还是一个可以接受一个字符串所有后缀的最小 DFA 。
要构造这个 DFA ,我们就要分配结束标记,表示在 DAG 上走到这个结点的时候,出现了该字符串的一个后缀。
先构建整个字符串的 SAM ,找到构建完成后的 \(last\) ,从 \(last\) 向根结点跳后缀链接,把路上遇到的每一个结点都打上结束标记。
这个做法的原理很简单:我们刚才讨论过了,从 \(last\) 跳后缀链接,可以访问字符串的所有后缀组成的每一个等价类( “算法原理” 一节中第 \(6\) 条第二段)。
最长公共后缀
原串 \(S\) 的两个子串的最长公共后缀是这两个子串所属 \(\text{endpos}\) 等价类对应结点在后缀树上 LCA 结点对应等价类中包含的最长的字符串。
跳后缀链接可以访问后缀,那么两条链的公共节点就是公共后缀啦。
统计子串
我们想要知道某个子串出现了几次,只需要知道它的 \(\text{endpos}\) 集合包含了几个元素就可以了。
显然,一个字符串的每一个前缀的所有后缀构成了这个字符串的所有子串,于是每一个子串只要成为原串某个前缀的后缀,出现次数就应该 +1 。
我们访问一个串的所有后缀十分方便——只要从它所属等价类对应的结点出发,跳后缀链接就行了。
注意到我们构建 SAM 的时候实际上是构建了串的每个前缀(按次序一位一位构造)。这样,我们可以在创建每一个新结点 \(cur\) 的时候给这个结点打上一个标记,表示这个结点是原串的一个前缀。
在建立好 SAM 之后,我们从刚才每一个打好标记的结点开始跳后缀链接,并把路径访问到的结点的标记 +1 ,表示这个前缀的所有后缀各出现了一次。操作完之后,每个结点被标记的次数就是这个结点的等价类对应的 \(\text{endpos}\) 集合大小了。不过这样做,最坏复杂度是 \(O(n^2)\) 的,显然不可以接受。
其实这个过程就是树上某个结点到根的路径点权 +1 ,考虑到每个结点的答案贡献一定来自它子树内的结点(只有它子树内的结点到根的路径才会经过它)。于是问题变成了子树求和,用树形 DP 可以做到 \(O(n)\) 的复杂度。
Part 5 解决问题
其实上面求每个子串的出现次数已经偏应用了,不过因为它太重要了,就把它放在了 “更多性质” 一节。
由于下面的题目是作者在不同时期写出的代码,马蜂(实现方式)略有不同,大家见谅。
下面的题目如果不做特殊说明,字符串均由嘤文小写字母组成。
Problem A 【模板】后缀自动机
upd:2024.9,评论区有同学说代码被叉了,似乎是不开long long见祖宗的问题?所以下面的代码仅供参考~
题目链接:Link
- 给你一个字符串 \(S\) ,求出每一个出现次数不为 1 的子串的出现次数乘上它的长度的最大值。
- \(1\leq |S|\leq 2\times 10^6\)
Solution
看到 “子串” 二字很容易联想到 SAM 吧,先对 \(S\) 建立起 SAM 。
在上面 “统计子串” 一节中,我们提到了计算一个子串出现次数的方式,现在考虑答案可能来自哪些子串。
显然在同一个等价类中,每一个子串的出现次数都相同,那么在这一堆相同的串中,显然只有最长的那个串可能构成答案。
那么我们可以在树形 DP 中顺便维护更新答案,总时间复杂度 \(O(n)\) ,转移方程如下:
Code
const int maxn=1000005;
char str[maxn];
int ans;
struct Suffix_Automaton{
int len[maxn<<1],link[maxn<<1];
int ch[maxn<<1][26];
int f[maxn<<1];
std::vector<int>v[maxn<<1];
int last,siz;
inline const void init(){
for(int i=0;i<=maxn*2-5;++i) v[i].clear();
memset(len,0,sizeof len);
memset(link,0,sizeof link);
memset(ch,0,sizeof ch);
link[0]=-1;
siz=last=0;
}
inline const void extend(char *str){
int n=std::strlen(str);
for(int _=0;_<n;++_){
int c=str[_]-'a',p=last,cur=++siz;
len[cur]=len[p]+1;
f[cur]=1;
while(p!=-1 && !ch[p][c]){
ch[p][c]=cur;
p=link[p];
}
if(p==-1) link[cur]=0;
else{
int q=ch[p][c];
if(len[q]==len[p]+1) link[cur]=q;
else{
int copy=++siz;
len[copy]=len[p]+1;
link[copy]=link[q];
for(int i=0;i<26;++i) ch[copy][i]=ch[q][i];
while(p!=-1 && ch[p][c]==q){
ch[p][c]=copy;
p=link[p];
}
link[q]=link[cur]=copy;
}
}
last=cur;
}
for(int i=1;i<=siz;++i) v[link[i]].push_back(i);
}
inline const int dfs(const int x){
for(int i=0;i<v[x].size();++i){
int y=v[x][i];
dfs(y);
f[x]+=f[y];
}
if(f[x]>1) ans=std::max(ans,f[x]*len[x]);
return f[x];
}
}sam;
signed main(){
scanf("%s",str);
sam.init();
sam.extend(str);
sam.dfs(0);
write(ans),putchar('\n');
return 0;
}
Problem B 【SDOI 2016】 生成魔咒
题目链接:Link
-
给你一个初始为空串 \(S\) ,\(n\) 次操作,每次向 \(S\) 的末尾添加一个数字 \(x_i\) 。
求每次添加 \(x_i\) 之后,串 \(S\) 中总共有多少个本质不同的子串。
譬如 “10,10,10” 有 3 个本质不同的子串:“10”,“10,10”,“10,10,10” 。
而 “1,2,1” 有 5 个本质不同的子串:“1”,“2”,“1,2”,“2,1”,“1,2,1” 。
-
\(1\leq x_i\leq 10^9,1\leq n\leq 10^5\)
Solution
还是子串问题,考虑 SAM 。
首先明确一个性质,向某个字符串末尾添加一个字符,一定不会导致子串数量减少,也就是原串 \(S\) 的子串不会消失。
于是我们只需要统计加入 \(x_i\) 产生的新子串有多少个,用 \(S\) 的不同子串数加上产生的新子串的数量得到答案。
考虑 \(\text{endpos}\) 集合,如果一个串是新产生的串,那么它在原串中一定没有出现过——它的 \(\text{endpos}\) 中一定只包含 \(|S|+1\) 这一个元素。同样,如果一个串的 \(\text{endpos}\) 并非只有 \(|S|+1\) 这一个元素,那么说明它在 \(S\) 中出现过,也就不是新产生的串。综上,可以得知:当且仅当一个串的 \(\text{endpos}\) 集合内有且仅有 \(|S|+1\) 这一个元素的时候,它是新产生的串。
现在任务变成了:找到 \(\text{endpos}\) 中只包含 \(|S|+1\) 这一个元素的串有几个。
显然,整个新串 \(S+x_i\) 的 \(\text{endpos}\) 一定只包含 \(|S|+1\) ,它是符合条件的一个串。考虑串 \(S+x_i\) 所属的等价类 \(cur\)(在 SAM 中,\(S+x_i\) 所属的结点是新建的 \(cur\) ,这里索性叫 \(cur\) 吧),\(cur\) 中包含的其他字符串的 \(\text{endpos}\) 一定和串 \(S+x_i\) 相同,这些串显然也符合条件。根据引理 \(2.2\) ,如果一个串不是 \(S+x_i\) 的后缀,那么它的 \(\text{endpos}\) 与 \(\text{endpos}(cur)\) 无交,这些串不可能成为答案。考虑 \(S+x_i\) 的不属于 \(cur\) 的后缀,设这些串属于等价类 \(cur'\) 。根据引理 \(2.1\) 有 \(\text{endpos}(cur)\subsetneq\text{endpos}(cur')\) ,也就是 \(cur'\) 至少包含一个非 \(|S|+1\) 的元素,这些串也不可能成为答案。
综上所述,\(\text{endpos}\) 中只包含 \(|S|+1\) 的串的数量就是 \(cur\) 中包含的字符串数量。
根据引理 \(4.2\) 的 “恰好覆盖” 性质,我们可以得出 \(cur\) 内包含的串的数量就是这些串长度覆盖的值域区间的长度,即 \(\text{len}(cur)-\text{minlen}(cur)+1\)。再用引理 \(5.1\) 转化一下,得到 \(\text{len}(cur)-\text{len}(\text{link}(cur))\) ,于是每次插入产生的新串数量就是 \(\text{len}(cur)-\text{len}(\text{link}(cur))\) 。
回到本题上来,我们知道了每次加入字符后产生的新子串数目,于是每次的答案可以递推得到,即:
总时间复杂度 \(O(n)\) 。
Code
const int maxn=100005;
struct Suffix_Automaton{
int len,link;
std::map<int,int>nxt;
}SAM[maxn<<1];
int siz,last,n,ans;
int SAM_extend(int c){
int cur=++siz;
SAM[cur].len=SAM[last].len+1;
int p=last;
while(p!=-1 && !SAM[p].nxt.count(c)){
SAM[p].nxt[c]=cur;
p=SAM[p].link;
}
if(p==-1) SAM[cur].link=0;
else{
int q=SAM[p].nxt[c];
if(SAM[q].len==SAM[p].len+1) SAM[cur].link=q;
else{
int copy=++siz;
SAM[copy].len=SAM[p].len+1;
SAM[copy].link=SAM[q].link;
SAM[copy].nxt=SAM[q].nxt;
while(p!=-1 && SAM[p].nxt.count(c)){
if(SAM[p].nxt[c]==q) SAM[p].nxt[c]=copy,p=SAM[p].link;
else break;
}
SAM[q].link=SAM[cur].link=copy;
}
}
last=cur;
return SAM[cur].len-SAM[SAM[cur].link].len;
}
signed main(){
read(n);
SAM[0].link=-1;
for(int i=1,q;i<=n;++i){
read(q);
ans+=SAM_extend(q);
write(ans),putchar('\n');
}
return 0;
}
Problem C 最长公共子串
题目链接:Link
- 给你两个字符串 \(s_1,s_2\) ,求这两个字符串的最长公共子串。
- \(1\leq |s1|,|s_2|\leq 2.5\times 10^5\)
题外话
讲道理,这个题其实在放 \(O(n\log n)\) 的 SA 做法,甚至有神仙用 \(O(n\log^2 n)\) 的前缀哈希过了的。
如下是这个题在 SPOJ 的讨论区:

Solution
对于这类统计多串子串类题目,我们有一个比较通用的做法:(伪)广义 SAM 。
广义 SAM 是指把 SAM 搬到 Trie 树上,类似于把 KMP 搬到 Trie 上变成 AC 自动机的原理,不过笔者不会 GSAM ,这里不做过多讨论。
伪广义 SAM 是指把多串用特殊字符分隔开,拼在一起建立一个 SAM ,然后通过做特殊标记的方式区分各个串,并统计多串信息。
譬如两个串 “abcbc” 和 “cbcab” 拼接后变成 “abcbc{cbcab”(这里用 “{” 分隔的原因是它的 ASCII 值紧随 “z” 之后,方便写代码)。
我们把它拼接在一起之后,情况就变成了这样:
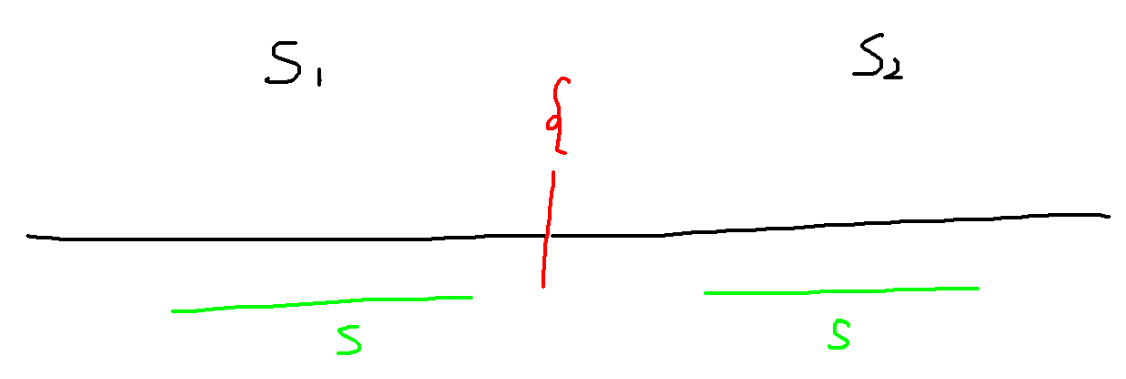
发现 “求公共子串” 变成了 “求出现 2 次及以上的最长子串” ,这个利用 \(\text{endpos}\) 的定义可以很简单的求出来。
写好代码,交了一发,WA 掉了,为什么呢?因为有这种毒瘤情况:
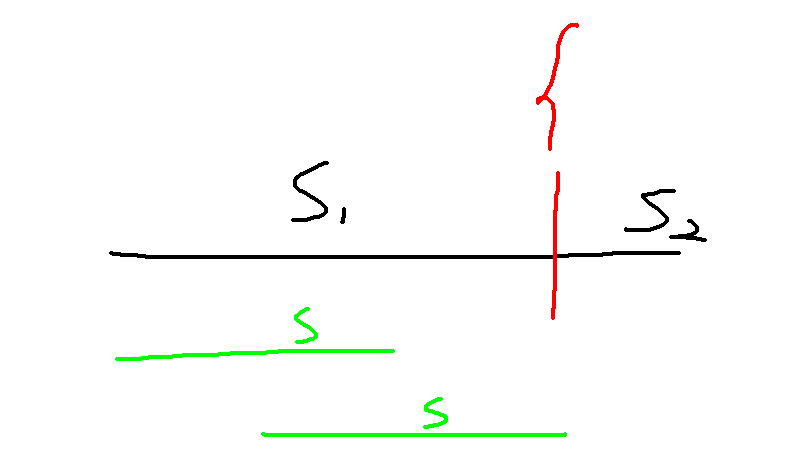
在这种情况下,这个出现两次的串都来自 \(s_1\) ,不能算作 “公共子串” ,但是我们的程序会把它统计上。
我们需要给来自 \(s_1,s_2\) 的串打上不同的标记,只有一个串的 \(\text{endpos}\) 内同时拥有两种标记,它才可以尝试去更新答案。
打标记和上传标记的方式和 “统计子串” 一节中提到的方式相同,即:树形 DP 。
这个算法的复杂度瓶颈在于树形 DP 的转移,对于 \(T\) 个串我们就要上传 \(T\) 种标记,花费 \(T\) 倍空间,不过由于这里 \(T=2\) 所以可以忽略掉啦。
如果 \(T\) 更多导致时空复杂度不可以接受,可以把标记数组压成一个 bitset ,带 \(\frac{1}{w}\) 的常数( \(w\) 是计算机位长),这是一个相当不错的优化。
总时间复杂度 \(O(\sum|s_i|+T\sum |s_i|)\) ,使用 bitset 则可以达到 \(O(\sum |s_i|+\frac{T\sum |s_i|}{w})\)。
Code
const int maxn=250005;
char s1[maxn],s2[maxn];
int ans;
struct Suffix_Automaton{
int len[maxn<<2],link[maxn<<2];
int ch[maxn<<2][27];
bool f[maxn<<2][2];
std::vector<int>v[maxn<<2];
int last,siz;
inline void init(){
link[0]=-1;
siz=last=0;
}
inline bool check(const int x){ return f[x][0]&f[x][1]; }//同时拥有两种标记
inline void extend(char *str,const int op){
int n=std::strlen(str);
for(int _=0;_<n;++_){
int c=str[_]-'a',p=last,cur=++siz;
len[cur]=len[p]+1;
f[cur][op]=1;
while(p!=-1 && !ch[p][c]){
ch[p][c]=cur;
p=link[p];
}
if(p==-1) link[cur]=0;
else{
int q=ch[p][c];
if(len[q]==len[p]+1) link[cur]=q;
else{
int copy=++siz;
len[copy]=len[p]+1;
link[copy]=link[q];
for(int i=0;i<27;++i) ch[copy][i]=ch[q][i];
while(p!=-1 && ch[p][c]==q){
ch[p][c]=copy;
p=link[p];
}
link[q]=link[cur]=copy;
}
}
last=cur;
}
}
inline void dfs(const int x){
for(int i=0;i<v[x].size();++i){
int y=v[x][i];
dfs(y);
f[x][0]|=f[y][0],f[x][1]|=f[y][1];//合并所有儿子的标记
}
if(check(x)) ans=std::max(ans,len[x]);//更新答案
}
}sam;
signed main(){
scanf("%s%s",s1,s2);
sam.init();
sam.extend(s1,0);
char qwq[1]={'{'};
sam.extend(qwq,0);
sam.extend(s2,1);
for(int i=1;i<=sam.siz;++i) sam.v[sam.link[i]].push_back(i);
sam.dfs(0);
write(ans),putchar('\n');
return 0;
}
Problem D 【TJOI 2015】弦论
题目链接:Link
-
给你一个字符串 \(s\) ,和两个参数 \(t,k\) ,求 \(s\) 中字典序第 \(k\) 小的子串,若不存在,输出 -1 。
若 \(t=0\) ,表示不同位置的相同子串算作一个。
若 \(t=1\) ,表示不同位置的不同子串算作多个。
-
\(1\leq |s|\leq 5\times 10^5,1\leq k\leq 10^9,0\leq t\leq 1\)
Solution
先构建 SAM 。我们知道,从 \(P\) 出发的 DAG 上的所有不同路径构成了字符串的所有子串,那么询问相当于找到 DAG 中第 \(k\) 小的路径。
考虑维护经过一个结点 \(v\) 的不同子串的数量,设为 \(f_v\) 。
在下面的过程中,初始的 \(u=P\) 。
-
初始的时候,要扫描 \(P\) 的每个儿子 \(v\) ,若 \(\sum f_v< k\) ,则无论如何也找不到 \(k\) 个不同的串,这说明无解,输出 -1 。
-
假设现在在点 \(u\) ,枚举 \(u\) 的每条出边,假设出边到达的结点是 \(v\) 。检查经过 \(v\) 的串的数量 \(f_v\) 是不是大于 \(k\) ,如果大于等于 \(k\) ,说明走 \(v\) 结点至少可以找到 \(k\) 个串,也就是第 \(k\) 小的串经过了 \(v\) ,去 \(v\) 继续寻找;否则说明经过 \(v\) 结点的不到 \(k\) 个串,第 \(k\) 小的串不经过 \(v\) 。如果 \(k\) 小串不经过 \(f_v\) ,那么 \(k\) 要减去 \(f_v\) ,表示我们已经找到了 \(f_v\) 个串,还要再找 \(k-f_v\) 个(这类似于使用主席树查询 \(k\) 小的原理)。
-
如果在某个结点,\(k=0\) ,说明我们已经找到了答案,退出程序即可。
到这里这个题就差不多了,现在考虑参数 \(t\) 对 \(f_v\) 的影响:
- 若 \(t=0\) ,那么对于每个串 \(m\) ,它所有的出现只算一次,也就是把它的 \(\text{endpos}\) 集合大小视为 1 。
- 若 \(t=1\) ,那么对于每个串 \(m\) ,它所有的出现每次都算,也就是按照正常的方式计算 \(\text{endpos}\) 大小。
最后一步,算 \(f_v\) 。根据定义,我们要求所有经过点 \(v\) 的路径的终点结点的 \(\text{endpos}\) 大小的和,这可以通过拓扑或者记忆化搜索快速求出。
总时间复杂度 \(O(n)\) 。
Code
char ch[maxn];
int t,k;
int f[maxn<<1],g[maxn<<1];//f 意义同上,g 表示 endpos 大小
struct Suffix_Automaton{
int link,len;
int ch[27];
}SAM[maxn<<1];
int siz,last;
void SAM_extend(const int c){
int cur=++siz,p=last;
g[cur]=1;
SAM[cur].len=SAM[p].len+1;
while(p!=-1 && !SAM[p].ch[c]){
SAM[p].ch[c]=cur;
p=SAM[p].link;
}
if(p==-1) SAM[cur].link=0;
else{
int q=SAM[p].ch[c];
if(SAM[q].len==SAM[p].len+1) SAM[cur].link=q;
else{
int copy=++siz;
SAM[copy].len=SAM[p].len+1;
SAM[copy].link=SAM[q].link;
for(int i=0;i<26;++i) SAM[copy].ch[i]=SAM[q].ch[i];
while(p!=-1 && SAM[p].ch[c]==q){
SAM[p].ch[c]=copy;
p=SAM[p].link;
}
SAM[q].link=SAM[cur].link=copy;
}
}
last=cur;//正常构建 SAM
}
bool vis[maxn<<1];
std::vector<int>to[maxn<<1];
void dfs(const int x,const int type){
for(int i=0;i<to[x].size();++i){
int y=to[x][i];
dfs(y,type);
if(type) g[x]+=g[y];//根据参数 t 求出 endpos 的大小
else g[x]=1;
}
}
int memory_search(const int x){//记忆化搜索,求 f
if(vis[x]) return f[x];
vis[x]=1;
for(int i=0;i<26;++i){
int y=SAM[x].ch[i];
if(y) f[x]+=memory_search(y);
}
f[x]+=g[x];//最后别忘了加上自己的 endpos 值!
return f[x];
}
void Build_parent(const int type){
for(int i=1;i<=siz;++i)
to[SAM[i].link].push_back(i);//建立后缀树
dfs(0,type);
g[0]=f[0]=0;//初始结点的 endpos 应该是空才对(虽然根据 SAM 的定义它应该是全集)
memory_search(0);
}
void Query(const int x){
if(k>f[x]){//实际上这个只有 x=P 的时候才会执行,因为 f[P] 最大,如果 k<f[P] ,那么一定有解
puts("-1");
exit(0);
}
if(k<=g[x]) exit(0);//到这个点之后已经找到了 k 个串,退出
k-=g[x];//减掉自身包含的串的数量
for(int i=0;i<26;++i){
int y=SAM[x].ch[i];//扫描每个儿子
if(!y) continue;
if(k>f[y]) k-=f[y];//减掉该儿子的 f 值
else{
putchar(i+'a');//目标串在这个儿子里,输出这条转移边对应的字母
Query(y);
}
}
}
signed main(){
scanf("%s",ch);
int len=std::strlen(ch);
read(t),read(k);
SAM[0].link=-1;
for(int i=0;i<len;++i) SAM_extend(ch[i]-'a');
Build_parent(t);
Query(0);
return 0;
}
Problem E 【AHOI 2013】差异
题目链接:Link
-
给定一个长度为 \(n\) 的字符串 \(S\) ,令 \(T_i\) 为它从第 \(i\) 个字符开始的后缀。求:
\[\sum_{1\leq i<j\leq n}\text{lenth}(T_i)+\text{lenth}(T_j)-2\times \text{lcp}(T_i,T_j) \]其中 \(\text{lenth}(a)\) 表示字符串 \(a\) 的长度,\(\text{lcp}(a,b)\) 表示字符串 \(a,b\) 的最长公共前缀。
-
\(1\leq n\leq 5\times 10^5\) 。
Solution
上面那个式子简单来说就是求所有子串长度之和减去所有子串的最长公共前缀之和。
由于 \(\sum_{1\leq i <j\leq n}\text{lenth}(T_i)+\text{lenth}(T_j)\) 是定值,可以先求出它来,剩下要处理的就是 \(2\times \text{lcp}(T_i,T_j)\) 。
至于定值的求法,利用高中数学 “数列” 一节中的知识可以得到,前面的式子等价于 \(\frac{n^3-n}{2}\) 。
现在考虑 \(2\times \text{lcp}(T_i,T_j)\) 怎么求,这个式子与 “所有子串” 相关,很自然的可以想到 SAM ,但是问题在于后缀树求的是 “最长公共后缀”,并不是题目中所求的 “最长公共前缀” 。
这个时候,如果我们把整个串翻转一下再插入 SAM ,就可以把 “最长公共后缀” 转换成 “最长公共前缀” 了,这也是 SAM 相关题目中的一个常用做法。
前面我们提到,后缀树上的每个结点包含的最长串是它不同子树中任意两个结点包含的所有串的最长公共后缀。那么显然可以考虑树形 DP ,即把每个点作为 LCA 考虑,求出这个结点对答案的贡献,然后对每个结点的贡献求和,就是所需的答案了。
注意到这个方法其实会重复计入答案,也就是说 \(T_i,T_j\) 和 \(T_j,T_i\) 都对答案有贡献,不过介于 \(T_i,T_j\) 和 \(T_j,T_i\) 的贡献相同,而题目中所求恰好是 2 倍的贡献。所以我们在求最后答案的时候,做树形 DP 求出来的这个差值不用乘 2 ,直接用定值减去即可。
总复杂度 \(O(n)\) 。
Code
const int maxn=500005;
int lenth;
char ch[maxn];
struct Suffix_Automaton{
int link,len;
int ch[27];
}SAM[maxn<<1];
int siz,last;
int f[maxn<<1],g[maxn<<1],sumdif;//f 标记了 endpos ,g 是子树求和
std::vector<int>Suffix_Tree[maxn<<1];//后缀树
void SAM_extend(const int c){
int cur=++siz,p=last;
SAM[cur].len=SAM[p].len+1;
f[cur]++;//标记
while(p!=-1 && !SAM[p].ch[c]){
SAM[p].ch[c]=cur;
p=SAM[p].link;
}
if(p==-1) SAM[cur].link=0;
else{
int q=SAM[p].ch[c];
if(SAM[q].len==SAM[p].len+1) SAM[cur].link=q;
else{
int copy=++siz;
SAM[copy].len=SAM[p].len+1;
SAM[copy].link=SAM[q].link;
for(int i=0;i<26;++i) SAM[copy].ch[i]=SAM[q].ch[i];
while(p!=-1 && SAM[p].ch[c]==q){
SAM[p].ch[c]=copy;
p=SAM[p].link;
}
SAM[q].link=SAM[cur].link=copy;
}
}
last=cur;
}//SAM 板子
void DP_on_Suffix_Tree(const int x){
g[x]=f[x];//先把子树和赋值为自己的 endpos
for(int i=0;i<Suffix_Tree[x].size();++i){
int y=Suffix_Tree[x][i];
DP_on_Suffix_Tree(y);
g[x]+=g[y];//子树求和
}
sumdif+=(g[x]-f[x])*f[x]*SAM[x].len;
//先算自己和所有子树之间产生的贡献
for(int i=0;i<Suffix_Tree[x].size();++i)
sumdif+=g[Suffix_Tree[x][i]]*(g[x]-g[Suffix_Tree[x][i]])*SAM[x].len;
//再算每一个子树和根以及其他子树的贡献
}
signed main(){
SAM[0].link=-1;
scanf("%s",ch);
std::reverse(ch,ch+(lenth=std::strlen(ch)));
for(int i=0;i<lenth;++i) SAM_extend(ch[i]-'a');
for(int i=1;i<=siz;++i) Suffix_Tree[SAM[i].link].push_back(i);
//翻转,建 SAM ,建后缀树
DP_on_Suffix_Tree(0);
//DP
write((lenth*lenth*lenth-lenth)/2-sumdif),putchar('\n');
// write(pow(lenth,3)/2-sumdif),putchar('\n');
//这样写就炸了 qwq
return 0;
}
最后提示一下大家,大整数幂千万不要偷懒使用 pow 函数。这是因为 pow 函数的实现基于牛顿迭代法,它求出的是一个逐渐逼近的近似解,如果答案过于巨大,便会由于精度问题,产生较大的误差(别问我为什么知道的,我对拍+Debug了 3h 才查出这个错来)。
Part 6 尾声
知识是无上限的,但是笔者的精力有。其实一开始我也只是想做一个简单的总结,不过本着 “做学问要严谨” 的信条,为了讲明白某些东西,这篇文章被一次又一次的加长、修改,直到今天的 18k 多字。
联赛在即,退役在即,我不想就这么无声无息的离去。我希望在我 OI 生涯的最后一段时光里,留下点什么……至少证明我存在过。
不知道以后看到这篇博文的我会不会对以前的自己竖起大拇指呢?不管怎么说,2 年的 OI 生涯,总是一段难忘的时光。
修改了保送政策以后,现在大部分老师家长都把竞赛扔进了垃圾堆,尤其是 OI 这种对文化课几乎无帮助的科目。我在身边人一遍又一遍重复着 “竞赛无用” 的情况下,坚持了两年。其实我心里很清楚,我并不具备保送的资格和潜质,OI 于我来说确实好像无用,但是这又有什么关系呢?
毕竟,人如果不趁着年轻去追求自己的热爱,那要青春做什么?这是一种热爱,一种信仰,而不是单纯的利益相关。
如果一个人是真正热爱 OI 的话,那么他应该是幸福的。因为他有机会放肆地去追求自己的热爱并为其献上最美好的年华。恰好,你我都是这样的人。
仅以此文,献给我的 17 岁。祝诸位 CSP 2021,NOIp 2021,rp++ 。

