二次扫描与换根法

在一类树上问题中，需要我们以每个结点为根统计一些信息。如果我们暴力枚举每个点为根，假设统计复杂度是 \(O(P)\) 的，那么总复杂度会达到 \(O(NP)\) 的级别，这样显然太慢了。这种问题我们一般通过两次扫描、换根的方法来优化复杂度，具体分为两步：

第一次扫描，任选一个结点为根进行树形 DP （也就是进行有根树 DP），此时我们回溯时自底向上统计信息到根。
第二次扫描，从刚才选择的根出发，进行一次 DFS 。这时需要推算出把根从当前结点换到儿子结点造成的影响，也就是转移方程。在进行递归前按照方程自顶向下把状态转移到儿子结点。

这样总复杂度就是 \(O(N)\) 的，大大优化了程序的效率。下面结合例题详细分析这个方法的应用。

Problem A [POI2008]STA-Station

给你一棵 \(N\) 个结点的树，求出一个结点，使得以这个结点为根的时候，所有结点的深度之和最大。
\(2\leq N \leq 10^6\)

一个很简单的暴力是从每个根出发进行一遍暴力 DP ，统计深度之和。

设 \(sum[x]\) 表示以 \(x\) 为根的子树中所有结点的深度之和，\(dep[x]\) 表示 \(x\) 的深度，那么可以写出如下的转移方程：

\[sum[x]=\sum_{y\in Son(x)} sum[y]+dep[x] \]

最后对 \(sum[x]\) 取 max 得到答案，不过这样复杂度是 \(O(N^2)\) 的，显然会超时，考虑优化。

不妨先随便假定一个根，进行一遍如上的树形 DP ，现在考虑“换根”操作造成的影响。

这里假定根是 5 。

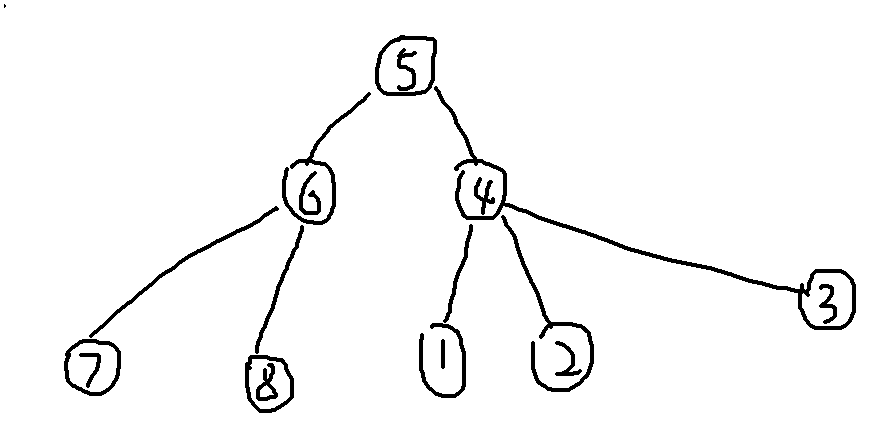
如果现在把根换到 4 呢？

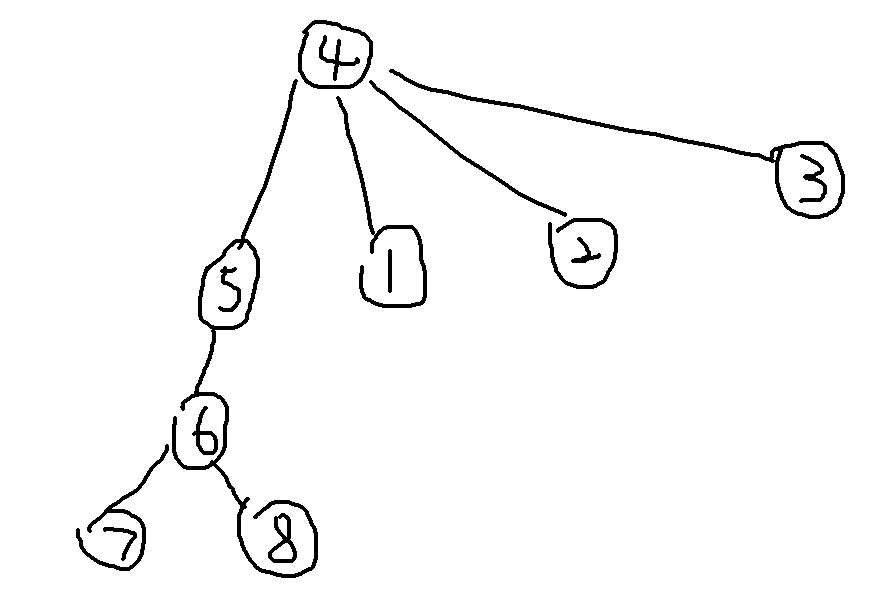
仔细观察，你就会发现 5 及其不包括 4 的子树内部的结点的深度都增加了 1 ，而 4 及其子树中的结点深度都减少了 1 。

于是可以写出换根的转移方程：

\[sum[y]=sum[x]-siz[y]+n-siz[y],y\in Son(x) \]

其中 \(siz[x]\) 表示在以 5 为根的时候，\(x\) 和他的子树内的结点数量。

于是可以写出代码：

const int maxn=1000005;

int n;
std::vector<int>v[maxn];

int dep[maxn],siz[maxn],f[maxn];//这里的f就是上面的sum数组
void dfs1(const int x,const int fa){
  dep[x]=dep[fa]+1;
  siz[x]=1;
  for(int i=0;i<v[x].size();++i){
    int y=v[x][i];
    if(y==fa) continue;
    dfs1(y,x);
    siz[x]+=siz[y];//统计出siz数组
  }
}
void dfs2(const int x,const int fa){
  for(int i=0;i<v[x].size();++i){
    int y=v[x][i];
    if(y==fa) continue;
    f[y]=f[x]+n-2*siz[y];//从父亲向儿子转移
    dfs2(y,x);
  }
}

signed main(){
  // freopen("simpleinput.txt","r",stdin);
  read(n);
  for(int i=1,x,y;i<n;++i){
    read(x),read(y);
    v[x].push_back(y),v[y].push_back(x);
  }
  dfs1(1,0);
  for(int i=1;i<=n;++i)
    f[1]+=dep[i];//统计出根的sum来
  dfs2(1,0);
  int ans,mx=0;
  for(int i=1;i<=n;++i)
    if(f[i]>mx) ans=i,mx=f[i];
  write(ans),putchar('\n');
  return 0;
}

Problem B CF1187E Painting

给定一棵 \(Ｎ\) 个结点的树，初始每个结点都是白点。

要求你做 \(N\) 次操作，每次选定一个与一个黑点相邻的白点，获得它所在的白点组成的连通块的大小的价值。

第一次操作可以任意选点，求可以获得的最大价值。
\(2\leq N\leq 2\times 10^5\)

分析一下题目性质，发现一旦选定初始点，不管我们之后扩展的顺序是怎样的，得到的权值都不会变（这个性质画画图很容易就可以发现）。

现在问题又转变成选择一个初始点，最大化从它扩展到全树所得的价值，经典二次扫描换根问题。

考虑每个结点，假设要扩展这个结点，可以得到多少权值，设这个值为 \(sum[x]\)，另外，设以 \(x\) 为根的子树大小为 \(siz[x]\) 。

那么很简单的，可以得到转移方程：

\[sum[x]=\sum_{y\in Son(x)}siz[y]+siz[x] \]

我们利用这个方程，求出任意一个结点为根时的 \(sum\) 值，然后进行换根，假设现在求出了 \(sum[1]\) 。

请看下图

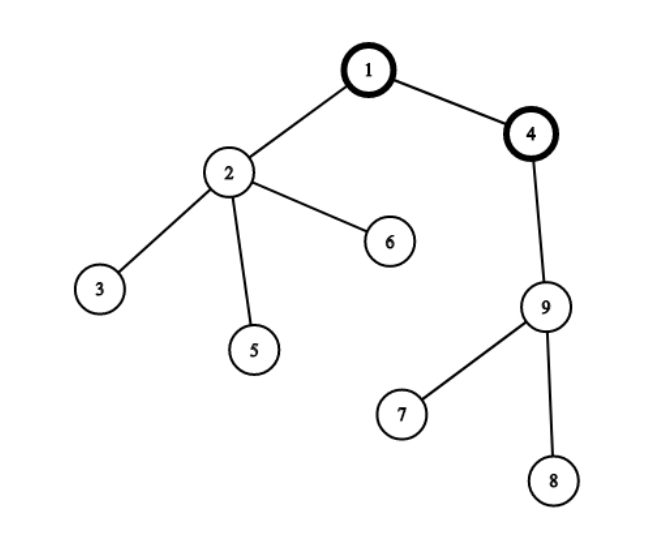
假设我们现在把根从 1 换到 4 ，然后扩展，那么我们多得到的权值就是 {1,2,3,5,6} 这个连通块的价值，但是同样我们失去了 {4,9,7,8} 这个连通块的价值。

因为我们是 dfs 进行转移，于是我们可以从父亲到儿子推出转移方程：

\[sum[y]=sum[x]-sum[y]+n-sum[y],y\in Son(x) \]

也就是说，我们从父亲转移到儿子的时候，得到了这个儿子子树大小的价值，损失了非该儿子子树的价值。

于是可以写出代码：

const int maxn=1000005;

int n;
std::vector<int>v[maxn];

int dep[maxn],siz[maxn],f[maxn];
void dfs1(const int x,const int fa){
  dep[x]=dep[fa]+1;
  siz[x]=1;
  for(int i=0;i<v[x].size();++i){
    int y=v[x][i];
    if(y==fa) continue;
    dfs1(y,x);
    siz[x]+=siz[y];
    f[1]+=siz[y];
  }
}
void dfs2(const int x,const int fa){
  for(int i=0;i<v[x].size();++i){
    int y=v[x][i];
    if(y==fa) continue;
    f[y]=f[x]-siz[y]*2+n;
    dfs2(y,x);
  }
}

signed main(){
  // freopen("simpleinput.txt","r",stdin);
  read(n);
  for(int i=1,x,y;i<n;++i){
    read(x),read(y);
    v[x].push_back(y),v[y].push_back(x);
  }
  f[1]=n;
  dfs1(1,0);
  dfs2(1,0);
  int mx=0;
  for(int i=1;i<=n;++i)
    mx=_max(f[i],mx);
  write(mx),putchar('\n');
  return 0;
}

Problem C Great Cow Gathering G

给定一棵 \(N\) 个结点的树，每个结点有点权 \(C_i\) ，每条边有长度 \(L_i\) 。

现在你要选择一个结点 \(j\) ，使得 \(\sum_{i\in tree} dis(i,j)\times C_i\) 最小，其中 \(dis(i,j)\) 表示两结点 \(i,j\) 之间的最短距离。
\(1\leq N\leq 10^5,0\leq C_i,L_i\leq 10^3\)

题目中每个结点都有可能成为结点 \(j\) ，可以通过换根法解决。

钦定 1 为根，于是通过一次 dfs 先求出当 1 为根时目标式子的值。

考虑把一个结点的 \(C_i\) 移动到它的父亲结点的花费，显然有 \(f=C_i\times val_{i,j},i\in Son(j)\) ，然后父亲结点 \(j\) 就有 \(C_i+C_j\) 个人，这些人再一起移动，不停的向父节点走，走到根，就可以得到目标式子的值，于是得到转移方程：

\[C_j=C_j+C_i,j\in Son(j) \]

\[f[1]=f[1]+C_i\times val_{i,j},i\in Son(j) \]

现在考虑换根造成的影响，假设现在根从 1 换到了它的一个儿子 \(x\) 。

那么不在 \(x\) 的子树中的结点就要多走 \(val_{1,x}\) 的距离才能到新的根 \(x\) ，而 \(x\) 的子树中的结点则少走 \(val_{1,x}\) 的距离，得到方程：

\[sum[y]=sum[x]+(C_1-C_y)\times val_{x,y} -C_y\times val_{x,y},y\in Son(x) \]

于是可以写出代码：

const int maxn=100005;

int n;
int w[maxn],f[maxn];//w就是上面的C_i
struct edge{ int y,val; };
std::vector<edge>v[maxn];

void dfs1(const int x,const int fa){
  for(int i=0;i<v[x].size();++i){
    int y=v[x][i].y;
    if(y==fa) continue;
    dfs1(y,x);
    w[x]+=w[y];//儿子的点权上传
    f[1]+=w[y]*v[x][i].val;//花费累积到根中
  }
}
void dfs2(const int x,const int fa){
  for(int i=0;i<v[x].size();++i){
    int y=v[x][i].y;
    if(y==fa) continue;
    f[y]=f[x]-w[y]*v[x][i].val+(w[1]-w[y])*v[x][i].val;
    dfs2(y,x);
  }
}

signed main(){
  // freopen("simpleinput.txt","r",stdin);
  read(n);
  for(int i=1;i<=n;++i)
    read(w[i]);
  for(int i=1,x,y,z;i<n;++i){
    read(x),read(y),read(z);
    v[x].push_back((edge){y,z}),v[y].push_back((edge){x,z});
  }
  dfs1(1,0);
  dfs2(1,0);
  int mi=999999999999999999999999999999;//会爆int，开大一点
  for(int i=1;i<=n;++i)
    mi=std::min(mi,f[i]);
  write(mi),putchar('\n');
  return 0;
}

Problem D Nearby Cows G

给一棵 \(N\) 个结点的树，每个结点的权值为 \(C_i\) ，边的长度为 1 ，对于每个结点 \(i\) 求出 \(\sum_{dis(i,j)\leq k}C_j\) ，其中 \(dis(i,j)\) 表示两节点之间的最短距离。
\(1\leq N \leq 10^5,1\leq k\leq 20\)

这题的出题人是老实人，直接把“求每个结点的值”写了出来，考虑换根法。

换根的转移思路并不难想，当根从 \(x\) 转移到他的儿子 \(y\) 时，答案加上 \(y\) 的子树中到 \(y\) 的距离为 \(k\) 的权值和，减去非 \(y\) 子树中到 \(x\) 的距离为 \(k\) 的结点的权值和。下图的例子展示了根从 1 转换到 4 ，\(k=1\) 的情况，红圈内为构成 4 的答案的结点，黑圈内为构成 1 的答案的结点。

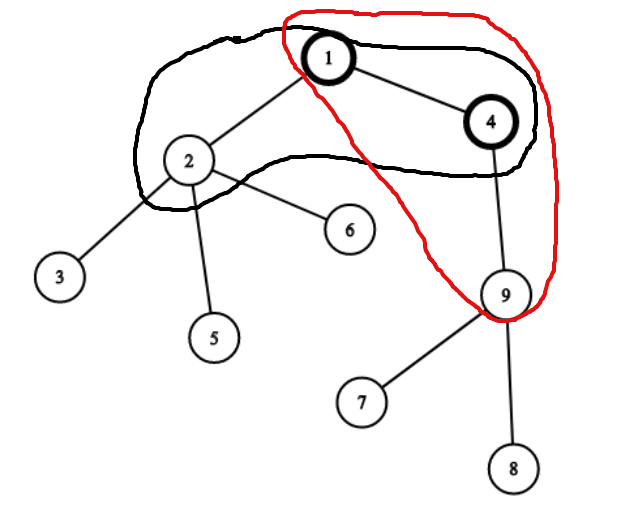
然而问题出现了，“\(x\) 的子树内到 \(x\) 距离为 \(k\) 的结点的权值和”这个东西维护起来比较鬼畜，因为距离大于 1 ，我们在 dfs 的时候没办法直接从儿子推导到父亲。

这时发现题目中给定的 \(k\) 比较小，只有 20 。可以考虑先维护“\(x\) 的子树内到 \(x\) 距离为 1 的结点的权值和”，这样我们就可以直接转移。假设 \(y\in Son(x)\) ，那么 \(y\) 的子树中到 \(y\) 的距离为 \(k\) 的结点到父亲 \(x\) 的距离就是 \(k+1\) 。然后可以通过 \(y\) 中维护的“距离为 \(k\) 的结点权值和”更新 \(x\) 中维护的“距离为 \(k+1\) 的结点的权值和”，这样我们的状态就可以从儿子推导到父亲啦！

设 \(f[x][k]\) 表示 \(x\) 的子树内到 \(x\) 的距离为 \(k\) 的结点的权值和，那么有如下转移方程：

\[f[x][k]=\sum_{y\in Son(x)}f[y][k-1] \]

通过这个方程，我们可以求出以一个结点为根的答案为 \(ans[i]=\sum^{k}_{i} f[x][i]\) 。

现在考虑换根转移，上面已经说过了转移的大体思路了，现在我们尝试把它写成方程的形式。

\[ans[y]=ans[x]+f[y][k]-f[x][k-1]+f[y][k-2] \]

为什么要加上 \(f[y][k-2]\) 呢？还记得我们对 \(f[x][k]\) 的定义吗？它表示的是 \(x\) 的子树内到 \(x\) 的距离为 \(k\) 的权值和，那么我们在减去 \(f[x][k-1]\) 的时候，其实把 \(y\) 子树内距离 \(y\) 距离为 \(k-2\) 的结点减掉了，而这些结点实际上应该被计入答案，所以我们要再加上这部分的贡献（简单容斥一下）。

于是可以愉快的写出代码了：

const int maxn=100005;

int n,k;
int f[maxn][22];
std::vector<int>v[maxn];

void dfs1(const int x,const int fa){
  for(int i=0;i<v[x].size();++i){
    int y=v[x][i];
    if(y==fa) continue;
    dfs1(y,x);
    for(int j=1;j<=k;++j)
      f[x][j]+=f[y][j-1];
  }
}
void dfs2(const int x,const int fa){
  for(int i=0;i<v[x].size();++i){
    int y=v[x][i];
    if(y==fa) continue;
    for(int j=k;j>=2;--j)//一定一定倒序循环，因为我们要用f[y][k]被更新之前的值做容斥
      f[y][j]+=f[x][j-1]-f[y][j-2];
    f[y][1]+=f[x][0];//距离为1不需要容斥
    dfs2(y,x);
  }
}

signed main(){
  // freopen("simpleinput.txt","r",stdin);
  read(n),read(k);
  for(int i=1,x,y;i<n;++i){
    read(x),read(y);
    v[x].push_back(y),v[y].push_back(x);
  }
  for(int i=1;i<=n;++i)
    read(f[i][0]);
  dfs1(1,0);
  dfs2(1,0);
  for(int i=1;i<=n;++i){
    int ans=0;
    for(int j=0;j<=k;++j)
      ans+=f[i][j];
    write(ans),putchar('\n');
  }
  return 0;
}

End

总的来说，DP 类问题需要的是思路的灵活变通，细节处理，最重要的是多练。

希望这篇博客能给大家带来一些灵感。

posted @ 2021-09-14 21:28 ZTer 阅读(413) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

欢迎光临 ZTer 的家！

二次扫描与换根法

二次扫描与换根法

Problem A [POI2008]STA-Station

Problem B CF1187E Painting

Problem C Great Cow Gathering G

Problem D Nearby Cows G

End

公告