虚实链剖分(LCT)
虚实链剖分 (Link-Cut-Tree)
公元 20XX 年,序列上的数据结构题已经被出题人玩烂了。这些毒瘤们凑在一起,想着如何更新题目的套路。突然,一位毒瘤出题人大开脑洞:“我们为什么不把序列问题搬到树上呢?”
于是树上毒瘤数据结构从此诞生,不过我们也有应对方法——树链剖分。
树链剖分分为三种:轻重链剖分、长链剖分、虚实链剖分(Link-Cut-Tree)。
这三种树链剖分本质上都是对树形结构的一种划分方式,不同的是这三者划分方式不同。
今天介绍一种树链剖分的方式——虚实链剖分。
Part 1 Problem
您需要写一种数据结构,维护 \(N\) 个点,点有点权,要求支持以下操作:
- 查询 \(u,v\) 两个点之间路径上点的权值的异或和,保证 \(u,v\) 连通。
- 连接 \(u,v\) ,如果已经连通,则无需再连接。
- 删除 \(u,v\) 之间的边,但不保证这条边存在。
- 把点 \(x\) 上的点权改为 \(y\) 。
Part 2 工作原理
比起轻重链剖分,虚实链剖分比较难理解,如果遇到凭看不能理解的地方,建议画个图帮助一下。
下面先介绍它的基本定义,然后一些基本操作,最后再说说代码实现细节。
一些基本定义
类似轻重链剖分,虚实链剖分的做法是把一个结点连向至多一个儿子的边划分为实边,连向其他儿子的边划分为虚边(可以全部划分为虚边)。
区别在于这个虚实可以动态变化(这就是语文里常讲的虚实结合),于是需要用更灵活的 Splay 来维护每一条由众多实边构成的实链。
因为我们可以动态划分这棵树,虚实链剖分的性质也更加优秀且灵活多变。
实际上,虚实链剖分维护的东西是一个森林而不是一棵树,它并不要求所有点之间连通。
在虚实链剖分的基础下,可以支持这些操作:
- 拎出一条链的信息以及修改这条链。
- 指定一个结点,使其成为树根。
- 连接、删除两节点之间的边(合并、分裂两棵树)。
- 维护两节点连通性(可以当高端的并查集使)。
- 另外一些牛逼的操作。
虚实链剖分(下面称为 LCT )的主要性质如下:
- 每一个 Splay 维护一条实链。要求这条实链上的结点深度序严格单调递增(显然为了满足这个要求,我们在一个结点深度相同的多个儿子中,最多只能选一个结点划分到实链上,可以一个都不选)。我们按照这个深度由小到大建立 Splay (也就是中序遍历这棵 Splay ,得到的每个点的深度递增啦)。容易发现,满足上面要求的划分方式不唯一。
- 每个结点包含且仅包含于一个 Splay 中。
- 上面说了,边分为实边和虚边,实边我们维护在 Splay 中,而虚边总是由一棵 Splay 指向另一个结点(这棵 Splay 中序遍历得到深度最小的点在原树中的父亲)。为了维护 Splay ,每一条虚边只可以由儿子访问父亲,而不可以由父亲访问儿子(一棵 Splay 中的结点不能有超过 2 个子节点,所以认父不认子)。
用一张图来说,对于一棵树,一种划分方式是这样的:
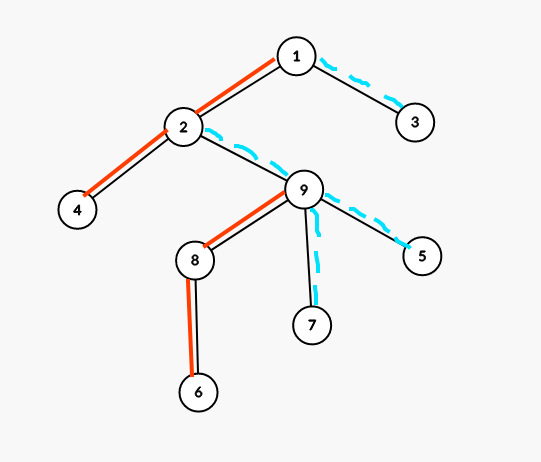
其中红色直线边表示实边,蓝色虚线边表示虚边。
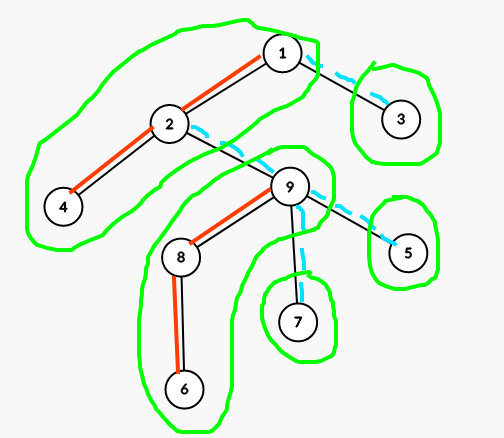
那么你应该建立如下图的 5 棵 Splay (每一棵都被绿色圈圈起来了):
一些基本操作
我写数据结构喜欢打包到结构体里,这里我们结合代码(针对上面问题),一个一个函数介绍吧。
首先创建一个结构体:
struct LCT{
int v,sum,tag;//v表示这个结点的权值,sum为异或和,tag是翻转标记(一会会说)
LCT *fa,*son[2];//splay要用的父亲和儿子
}*null,*ptr[maxn];//null用来防止访问NULL导致RE,*ptr[]是每个结点的指针
void access(LCT *x)
它是 LCT 最最核心的操作,其他操作都要基于它哦~
这个操作表示“打通 \(x\) 到根的路径”,即使得一棵中序遍历从根开始,到 \(x\) 结束的 Splay 出现。
一个更形象的说法是:使得一条以根为开头,到 \(x\) 结束的实链出现。
下面的图片参考了 YangZhe 的论文 。(有这么好的图干嘛还自己画呢?)
假设现在有一棵树,对实边和虚边的划分是这样的(虚线为虚边)。
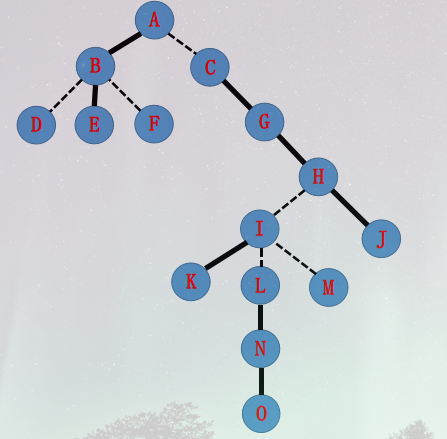
那么所构成的LCT可能会长这样(只是举个例子,实际上有很多种划分方式,不过只要满足上面的 3 条性质,就没问题)。

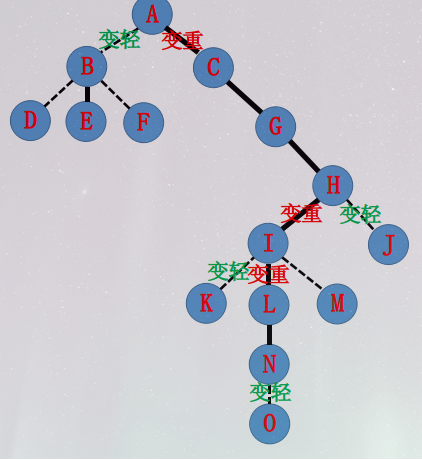
假设我们要 access(N) ,把 \(A-N\) 的路径拉起来变成一条实链。
因为性质 1 ,每个结点只能有一条实边,所以我们要把 \(A-N\) 路径上的虚边变为实边,再把每个点到该路径以外的实边变虚。
所以最后,这棵树的实虚边应该这样划分:
怎么实现呢?应该从 \(N\) 一步步往上拉。
首先 splay(N) 把 \(N\) 变成当前 Splay 的根。
因为我们希望出现的这条链的结尾是 \(N\) 而不是 \(O\) ,所以要把 \(N-O\) 的这条实边变虚。
按深度 \(O\) 在 \(N\) 下面,那么 splay(N) 之后,\(O\) 应该在 \(N\) 的右子树,单方面把 \(N\) 的右儿子置为空(认父不认子)。
现在应该是这样( \(O\) 的父亲还是 \(N\) ,但是 \(N\) 不认 \(O\) 这个儿子了):
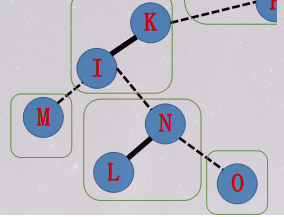
\(N\) 这棵 Splay 的虚边指向 \(I\) ,splay(I)(原树上是 \(L\) 的父亲)。
为了满足性质 1 ,原来在 \(I\) 下方的实边 \(I-K\) 要变虚,同样是去掉右儿子。
现在 \(I-L\) 可以变实了。因为 \(L\) 的深度应该大于 \(I\) ( \(L\) 的虚边指向 \(I\) ),应该把 \(I\) 的右儿子置为 \(N\) 。
然后就变成这样:
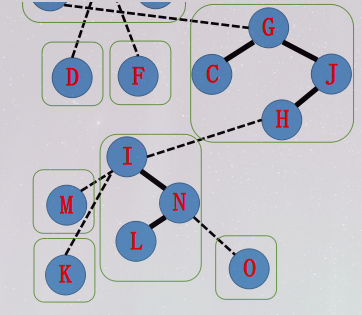
然后如法炮制,\(I\) 指向 \(H\) ,splay(H),把 \(H-J\) 变虚( \(H\) 单方面不认右儿子 \(J\) ),然后把右儿子置为 \(I\) 。
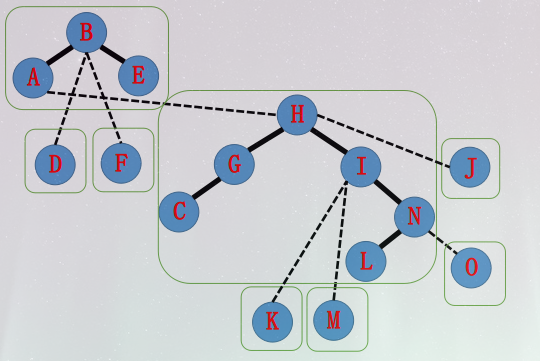
\(H\) 指向 \(A\) ,splay(A),把 \(A-B\) 变虚( \(A\) 单方面不认右儿子 \(B\) ),然后把右儿子置为 \(H\) 。
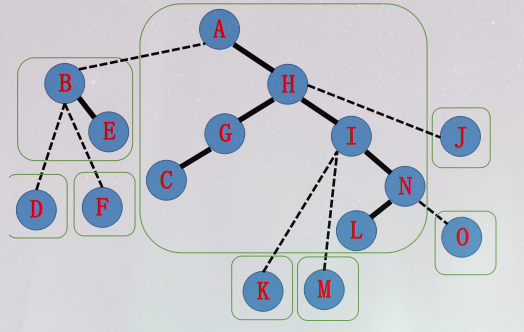
现在 \(A-N\) 的路径已经在一个 Splay 里啦!好耶!
这个过程看似很复杂,其实代码写起来挺简单的。
总结一下,上面的操作一共有 4 步:
- 转到根。
- 改右儿子。
- 更新信息。
- 把操作结点变成当前结点的父亲。
- 重复 1 。
代码:
inline void access(LCT *x){
LCT *y=null;
while(x!=null){
splay(x);
x->son[1]=y;
update(x);
y=x,x=x->fa;
}
}
void makeroot(LCT *x)
void split(LCT *x,LCT*y)
把一个结点到根的路径拉起来还不够,因为我们又不一定只查询某个点到根的路径。
这个时候就用到了“换根”操作,也就是 makeroot 。
如果把根换成 \(x\) ,然后再把 \(y\) 到根的路径拉起来,那不就是相当于拉出来 \(x,y\) 之间的路径吗?
Q:为什么不能直接拉出 \(x,y\) 的路径?
A:因为 \(x,y\) 不一定是祖孙关系,也就是这两个点的 LCA 既不是 \(x\) ,也不是 \(y\) ,那么这两个点之间的路径深度就不是单调递增的,根据性质 1 ,这样的实链不可以出现在一个 Splay 中,这时就要用 makeroot 操作改一下深度关系,然后再拉起来。
注意到 access(x) 之后,\(x\) 显然一定是这个 Splay 中深度最大的点,splay(x) 之后,\(x\) 一定没有右子树(性质 1 )。这时翻转整个 Splay ,\(x\) 反倒没了左子树,这样它就成了深度最小的点(根结点)。这时我们就可以 access(y) ,把 \(x,y\) 的路径拉起来啦!
代码:
inline void Rev(LCT *x){ LCT *t=x->son[0];x->son[0]=x->son[1],x->son[1]=t;x->tag^=1; }//打翻转标记
inline void makeroot(LCT *x){ access(x),splay(x),Rev(x); }
inline void split(LCT *x,LCT *y){ makeroot(x),access(y),splay(y); }//先换根,然后拉起
void findroot(LCT *x)
作用是找结点 \(x\) 原树(在森林中)的树根是谁,主要是用来判断连边和断边操作是否合法,如果保证合法,则不需要这个函数(事实证明这玩意挺慢的)。
要找原树的树根,可以先打通 \(x\) 到根的路径,这个时候 \(x\) 和树根一定在一棵 Splay 中,我们只要找到中序遍历第一个结点就是原树的树根了。
代码:
LCT *findroot(LCT *x){
access(x),splay(x);
while(x->son[0]!=null)
push_down(x),x=x->son[0];//push_down(x) 下传翻转标记,否则可能出错
splay(x);
return x;
}
void Link(LCT *x,LCT *y)
作用是连接 \(x,y\) 两个结点(合并森林中两棵树)。
森林中一棵树的树根的父亲一定是空结点,我们可以先把 \(x\) 结点变成根,然后向 \(y\) 连一条虚边。
代码:
inline void Link(LCT *x,LCT *y){ makeroot(x);if(findroot(y)!=x) x->fa=y; }
//如果已经在一个树中,不再连边,如果连边合法,splay(x)之后,从x到y连一条虚边
//如果你能保证连边合法,不 findroot(x) 更快
inline void Link(LCT *x,LCT *y){ makeroot(x),x->fa=y; }
void Cut(LCT *x,LCT *y)
作用是断开 \(x,y\) 两个结点(断开一条边以分裂一棵树)。
我们可以先把 \(x,y\) 搞到一条实链上,如果 \(x,y\) 有连边的话,那么应该满足如下性质:
- \(y\) 没有左儿子,如果 \(y\) 有左儿子,那么中序遍历 \(x\) 的下一个结点就不是 \(y\) ,即原树上 \(x,y\) 没有连边。
- \(y\) 的父亲是 \(x\) ,这个没什么好说的吧。
findroot(y)==x这表明 \(x,y\) 在森林中同一棵树上。
如果给出的 \(x,y\) 满足这三条性质,那么把 \(x\) 的右儿子,\(y\) 的左儿子置为空结点即可。
代码:
inline void Cut(LCT *x,LCT *y){
makeroot(x);
if(findroot(y)==x && y->fa==x && y->son[0]==null){
y->fa=x->son[1]=null;
update(x);//因为删掉了x的一个儿子,更新一下它
}//注意findroot的时候有access和splay操作,此时x为根,y和x在同一实链上
}
//同样,如果你可以保证删除边合法的话,可以不判断,减小常数
inline void Cut(LCT *x,LCT *y){ split(x,y),y->fa=x->son[1]=null,update(x); }
Part 3 代码实现
Q:听了这么多,好像明白了,不过我还有一个问题:为什么要用 Splay 维护区间翻转呢?FHQ-Treap 也支持区间翻转,而且代码短也好写,为什么不用呢?
A:没错,我们使用平衡树的目的就是为了区间翻转,不用 FHQ-Treap 是因为它会导致复杂度错误。正常情况下,LCT 操作一次的复杂度应该是 \(O(logn)\) 的,如果使用 FHQ-Treap ,则复杂度会多一个 \(log\) ,变成 \(O(log^2n)\) ,加上自带的巨大常数,这是我们不能接受的。 Splay 的复杂度经过了系统证明(势能分析法),如果你想深入了解一下,可以看这个。
好了,问题差不多都解决了,下面可以上代码啦!
// 本代码针对洛谷P3690 动态树,也就是Part 1中的问题
const int maxn=300005;
using namespace zhangtao;
int n,m;
struct LCT{
int v,sum,tag;
LCT *fa,*son[2];
}*null,*ptr[maxn];
inline bool notroot(LCT *x){ return x->fa->son[1]==x || x->fa->son[0]==x; }
inline void update(LCT *x){ x->sum=x->son[0]->sum^x->son[1]->sum^x->v; }
inline void Rev(LCT *x){ LCT *t=x->son[0];x->son[0]=x->son[1],x->son[1]=t;x->tag^=1; }
//如果你维护的信息与具体来自左右儿子中哪一个有关,那么也要交换这个信息哦
//我已经踩了 SDOI 2011 染色 的坑了
inline void push_down(LCT *x){
if(x->tag){
if(x->son[0]!=null) Rev(x->son[0]);
if(x->son[1]!=null) Rev(x->son[1]);
x->tag=0;
}
/*
一些题目需要打更多的标记,这时你可以写在这里哦
记住无论是什么题,都要先下传翻转标记!
if(x->tag2){
do sth.
}
*/
}
inline bool get_which(LCT *x){ return x->fa->son[1]==x; }
void rotate(LCT *x){
LCT *y=x->fa,*z=y->fa;
int k=get_which(x);
LCT *w=x->son[!k];
if(notroot(y)) z->son[get_which(y)]=x;x->son[!k]=y,y->son[k]=w;
if(w!=null) w->fa=y;y->fa=x,x->fa=z;
update(y),update(x);//如果你要更新信息的话,写在这里
}
void splay(LCT *x){
LCT *now=x;
std::stack< LCT* >st;
st.push(now);
while(notroot(now)) st.push(now=now->fa);
while(st.size()) push_down(st.top()),st.pop();
//splay之前先把到根路径上的标记下传干净,如果写在rotate里容易错,这么写是我感觉最保险的写法
//建议普通splay区间翻转的时候也这么写
while(notroot(x)){
LCT *y=x->fa,*z=y->fa;
if(notroot(y)) rotate(get_which(y)^get_which(x)?x:y);
rotate(x);
}
update(x);//最后更新一下
}
inline void access(LCT *x){
LCT *y=null;
while(x!=null){
splay(x);
x->son[1]=y;
update(x);
y=x,x=x->fa;
}
}
inline void makeroot(LCT *x){ access(x),splay(x),Rev(x); }
LCT *findroot(LCT *x){
access(x),splay(x);
while(x->son[0]!=null)
push_down(x),x=x->son[0];
splay(x);
return x;
}
inline void split(LCT *x,LCT *y){ makeroot(x),access(y),splay(y); }
inline void Link(LCT *x,LCT *y){ makeroot(x);if(findroot(y)!=x) x->fa=y; }
inline void Cut(LCT *x,LCT *y){
makeroot(x);
if(findroot(y)==x && y->fa==x && y->son[0]==null){
y->fa=x->son[1]=null;
update(x);
}
}//和上面说的都是一样的
void Init(){
read(n),read(m);
null=new LCT;
null->fa=null->son[0]=null->son[1]=null;
null->v=null->sum=null->tag=0;//经典防RE空指针
for(int i=1,v;i<=n;++i){
read(v);
ptr[i]=new LCT;
ptr[i]->v=v;//初始化点权
ptr[i]->sum=ptr[i]->tag=0;
ptr[i]->fa=ptr[i]->son[0]=ptr[i]->son[1]=null;
}
}
signed main(){
// freopen("simpleinput.txt","r",stdin);
Init();
while(m--){
int type,x,y;
read(type),read(x),read(y);
switch(type){
case 0 :{
split(ptr[x],ptr[y]);//拉出x->y的链,此时y为Splay的根,输出y的sum值
write(ptr[y]->sum),putchar('\n');
break;
}
case 1:{
Link(ptr[x],ptr[y]);//连边
break;
}
case 2:{
Cut(ptr[x],ptr[y]);//删边
break;
}
case 3:{
splay(ptr[x]);//如果要修改的话,先把这个结点转到所在Splay的根,这样它的值就不会再用来更新他的祖先结点了
ptr[x]->v=y;//修改一下
update(x);//更新自己,搞定!
}
}
}
return 0;
}
本博客部分借鉴了 FlashHu's Blog 。我也是从那篇博客学会了 LCT ,那里有一些代码实现的细节,大家可以去看看。
如果这篇博客可以让您学会 LCT 的话,是我莫大的荣幸,期望您能高抬贵手点个赞或者评论一下。
如果您还是有一些疑问的话,欢迎在下方评论区提出您的问题,或者加博主 QQ 联系(在侧边栏有哦),我会尽力为您解答。

