Splay 详解
Splay (也许不)详解
前言
在我之前的博文中,已经介绍了平衡树的一种实现方式:树堆(Treap),今天再来介绍一种功能更强大,实现更方便,常数更大的平衡树——伸展树(Splay)。如果您还不知道平衡树是甚么,请移步这里。
背景介绍
伸展树 (Splay Tree),也叫分裂树,是一种自平衡二叉搜索树,它能在 \(O(log n)\) 内完成插入、查找和删除操作。它由丹尼尔·斯立特 (Daniel Sleator) 和 罗伯特·恩卓·塔扬 (Robert Endre Tarjan) 于 1985 年发明(怎么又是 Tarjan 巨佬)。
假设想要对一个二叉查找树执行一系列的查找操作。为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法, 在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。splay tree应运而生。Splay tree 是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去,这个操作称为“伸展”。
以上来自百度百科。
Part 1 Splay 原理
Splay 说到底是个平衡树,最终目的是要保持树高为 \(log\) 级别。Splay 实现平衡的方式和 Treap 大同小异——旋转!
借用一下我之前 Treap 博客中的图文:
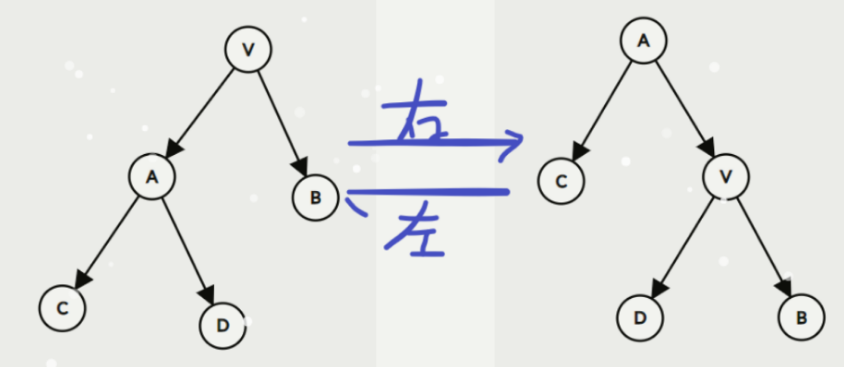
我们用一个数组 Val[x] 来表示节点 x 的权值,现在假设我们要交换 V 和 A 两个节点的位置。
根据 BIT 的性质,有: Val[C]<Val[A]<Val[D]< Val[V]<Val[B] 。
先不管那么多,直接交换 A 和 V 的位置一发,那么因为 Val[A]<Val[V],V 势必要成为 A 的右儿子。此时,C 为 A 的左儿子,B 为 V 的右儿子不需要调整,剩下一个 D 节点,因为 Val[D]<Val[V] ,D 成为 V 的左儿子。
这样一番操作之后,我们就把原来在上方的节点 V 转到了它左儿子 A 的下方(右旋)。同样的,也可以把上方节点转到右儿子下方(左旋)。
那么如上是二叉搜索树的旋转操作,对于任何一棵二叉搜索树,都满足这种可旋转的性质。
在背景介绍中提到过,Splay 的核心操作是“伸展”,也就是把某个节点搬到树根去。当然了,从树上某个节点出发,一定可以找到一条到树根的路径,只要不停的沿着这个路径一顿旋转,把所需节点转上去就行了。
但是事实没有这么简单。
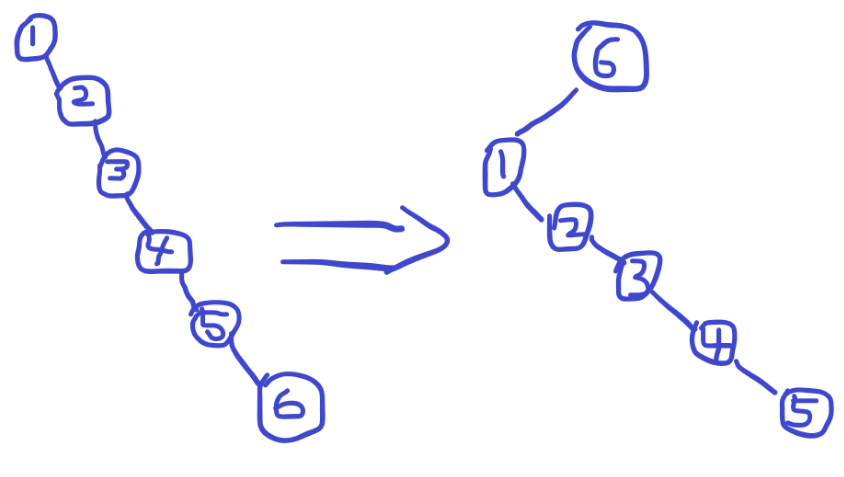
如果你面前是这样一棵树。假设你要把 6 转到根,发现转完之后,树高还是 \(n\) 级别,没有变化。

(本图来自平衡树与LCT讲课.ppt,作者:zyb)
解决办法是有的:现在引入一个重要操作——双旋
设当前点为 \(q\) ,父亲为 \(p\) 。如果 \(q\) 和 \(p\) 同是父亲的左儿子或同是右儿子,就先转 \(p\) 再转 \(q\),否则就转两次 \(q\) 。效果:将长链尽可能“折叠”,使得树高尽量减小,达到自平衡的目的(具体为什么您得问 Tarjan 老爷子了)。
同样是把 6 转到根:
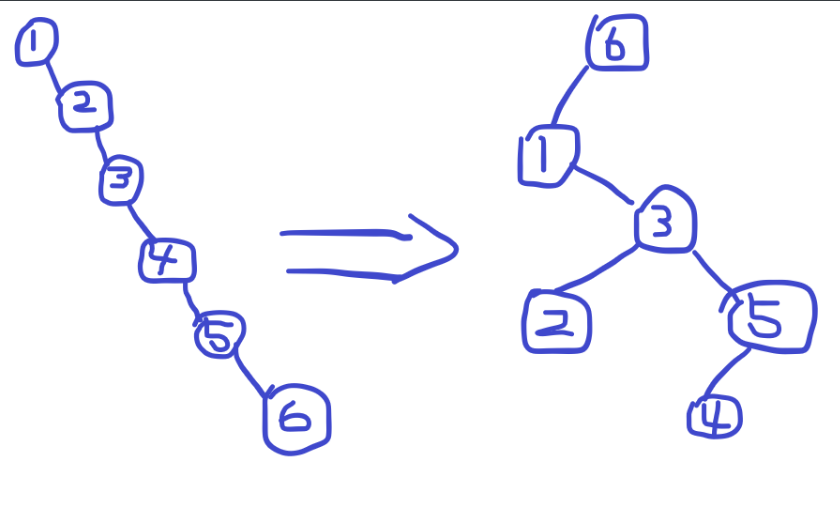
发现树变矮了(这个图变矮得不明显,这都怪 zyb)!于是我们可以使用这样的“双旋”来维持平衡。具体操作就是:在每次插入、查询之后,都把目标节点伸展调整到根节点。

(本图来自平衡树与LCT讲课.ppt,作者:zyb)
Part 3 Splay 的作用、构建 Splay
当然了,Splay 因为其优秀的可扩展性,获得了一个“序列之王”的美誉,不过今天我们只把他当作一棵平衡树来讨论。作为一棵平衡树,Splay 支持向数据库中插入一个数,删除一个数,查询数据库内排名为 \(k\) 的元素,元素 \(x\) 的排名,比 \(x\) 大的最小的数或比 \(x\) 小的最大的数。所有这些操作的复杂度都是 \(O(log(n))\) 。
首先声明一个结构体:
struct Splay{
int cnt,value,size;//cnt表示值为value的有几个,value为节点的关键码,size表示子树+该节点总大小
Splay *son[2],*fa;//表示左右儿子和父亲是谁
};
Splay *root,*null;//root是根,null是用来防止访问空节点导致RE用的
最重要的旋转操作:
因为我们要进行“双旋”,所以要知道儿子节点、父亲节点、爷爷节点之间的父子关系如何(为左儿子还是右儿子)。如果儿子节点和父亲节点同为其父亲的左儿子或右儿子,则需先转父亲,否则先转儿子。
inline bool get_which(Splay *x){
return x->fa->son[1]==x;
}//返回x是它父亲的左儿子还是右儿子
inline void update(Splay *x){
x->size=x->son[0]->size+x->son[1]->size+x->cnt;
}//更新x节点的子树信息
inline void rotate(Splay *x){
Splay *fa=x->fa;
Splay *grandfa=fa->fa;
int which_son=get_which(x);
if(grandfa!=null)
grandfa->son[get_which(fa)]=x;
x->fa=grandfa;
fa->son[which_son]=x->son[which_son^1];
x->son[which_son^1]->fa=fa;
x->son[which_son^1]=fa;
fa->fa=x;//调整一下父子关系,具体可以看上面的图理解
update(fa);//旋转之后父亲节点深度更深,先更新它
update(x);//然后更新儿子
}
inline void splay(Splay *x,Splay *target){//意为把x伸展为target的儿子
while(x->fa!=target){
Splay *fa=x->fa;
Splay *grandfa=fa->fa;
if(grandfa!=target)//如果爷爷就是目标位置,那么只要转一次就行了
rotate( get_which(fa)^get_which(x) ? x :fa );//根据父子关系判断先转谁
rotate(x);
}
if(target==null) root=x;//伸展到根,更新根是x
}
插入一个节点:
类似 Treap 的插入原理,先从根开始递归,依据关键码大小找到需要插入的位置,直接插入即可。唯一需要注意的是插入完了之后需要伸展一发,把新插入节点伸展到根的位置。
inline void insert(int x){
Splay *now=root,*fa=null;//从根开始比较
while(now!=null && now->value!=x){//没找到空位置或者没找到关键码为x的节点
fa=now;
now=now->son[x>now->value];
}
if(now!=null) now->cnt++;//代表找到关键码为x的节点,cnt++就行
else{//没找到,新建一个value为x的节点
Splay *p=new Splay;
if(fa!=null) fa->son[x>fa->value]=p;
p->fa=fa;
p->value=x;
p->size=p->cnt=1;
p->son[0]=p->son[1]=null;//这些都是初始化结构体里那些信息,不赘述
splay(p,null);//建完了,伸展到根
return;
}
splay(now,null);//伸展到根
}
查排名、查 k 小,查前驱、查后继:
平衡树基本操作,都是依靠二叉搜索树性质实现。如果不懂,可以看看这篇博客,在平衡树基于 Treap 的实现中我详细讲过了这几种操作,这里不再重复。
void search(int x){
Splay *now=root;
if(now==null) return;
while(now->son[x>now->value]!=null && x!=now->value)
now=now->son[x>now->value];
splay(now,null);
}//找到x的位置,并把它伸展到根
Splay* get_pre(int x){
search(x);//找到x,并把x伸展到根
Splay *now=root->son[0];//左子树里的都小于x,先去左子树。
while(now->son[1]!=null)//疯狂往右子树递归(右子树中的数更大)
now=now->son[1];
return now; //直到找不到右儿子,now即为x的前驱
}
Splay* get_back(int x){
search(x);
Splay *now=root->son[1];
while(now->son[0]!=null)
now=now->son[0];
return now;//后继同理
}
//这么写是基于树中有关键码为x的节点,找到这个节点并把它伸展到根。
//这时,比x小的树都在它左子树中,比x大的都在右子树中,于是递归左/右子树,找到最大/最小的数即为x的前驱、后继
//所以查x的前驱后继之前,要先插入一个x,查完了之后再删掉它
...在 main() 函数中{
insert(x);
get_pre(x);
get_back(x);
_delete(x);
}
int get_num(int x){//查k小
Splay *now=root;//从根出发
while(1){
if(x<=now->son[0]->size)//左子树有多于k个元素,去左子树找
now=now->son[0];
else{
x-=(now->son[0]->size+now->cnt);//减掉左子树和当前节点元素数
if(x<=0) return now->value;
//如果x<=0,有 son[0]->size < x <= son[0]->size+now->cnt,也就说明k小就是当前节点的value
else now=now->son[1];//去右子树找
}
}
}
int get_rank(int x){//查x的排名
search(x);
return root->son[0]->size+1;//找到x,旋转到根,左子树中的节点都比他小,他的排名自然是son[0]->size+1
}
最后是删除操作:
为什么把删除操作放到最后呢?因为这个是全 Splay 中最复杂的一个操作,我当时理解了好久才明白。。。
假设要删除 x ,先找到 x 的前驱、后继。把 x 的前驱调整到根,x 的后继调整到根的右儿子,然后直接干掉根的右儿子的左儿子。此时,被干掉的一定是 x ,而且 x 一定没有儿子,不用讨论更新子节点的问题。

其实上面的操作分为两条:
- 按上述方法调整之后,根的右儿子的左儿子一定是 x 。
- 按上述方法调整之后,x 没有儿子。
我们一条一条来看,先来证明第一条性质。
证明:
设上述一顿操作之后的根节点是 p ,根的右儿子是 q ,q 的左儿子是 v 。
依据二叉搜索树的性质,p 右子树中的节点一定比 p 大。v 在右子树中,v 一定大于 p ,同时 v 又在 q 的左子树中,同理可得 v 一定小于 q ,即 p<v<q 。
而我们是根据 x 求出的前驱、后继 p、q 。根据前驱、后继的定义,满足 p<v<q 的 v 的值有且仅有一个,那就是 x ,所以,此时 v 代表的节点一定是 x 。
证毕。
再来证明第二条性质。
反证法:
设上述一顿操作之后根节点是 p ,根的右儿子是 q ,q 的左儿子是 v 。
如果 v 有左儿子,设其为 u ,则 u<v 。
又因为 v 在 p 的右子树中,则 u 也在 p 的右子树中,有 p<u<v 。
根据第一条性质,p 是 v 的前驱。如果 p,u,v 同时满足上面的不等式,那么 v 的前驱应该为 u ,与事实矛盾,不成立。故不存在这样的节点 u ,也就是 x 没有左子树。
同理,如果 v 有右儿子,设其为 u ,则 u>v 。
又因为 v 在 q 的左子树中,则 u 也在 q 的左子树中,有 v<u<q 。
根据第一条性质,q 是 v 的后继。如果 q,u,v 同时满足上面的不等式,那么 v 的后继应该为 u ,与事实矛盾,不成立。故不存在这样的节点 u ,也就是 x 没有右子树。
如果您还没理解,可以尝试画画图。证明部分我自认为是比较充分了。
如果找到了 x 的位置,并且它还没有左右子树,就可以直接删除它了。
inline void clear(Splay* &x){
x->son[0]=x->son[1]=x->fa=null;
x->value=x->cnt=x->size=0;
}//删除x节点,如果使用内存池的话,可以顺便回收一下内存,这里我没有回收(懒
void _delete(int x){
Splay *pre=get_pre(x),*back=get_back(x);//找到前驱后继
splay(pre,null);
splay(back,pre);//伸展,调整位置
if(back->son[0]->cnt>1){
--back->son[0]->cnt;
splay(back->son[0],null);//如果关键码为x的节点有多个,删掉其中一个,然后把x调整到根
}else{//只有一个,直接删掉即可
back->son[0]=null;
clear(back->son[0]);
}
}
Part 4 后记
其实我从 7 月 14 号就开始尝试写 Splay ,中间无数次写挂,无数次鸽掉,直到 7 月 21 号才调出来,今天才来写博客。感觉写的也不是很清楚,不过个人水平有限暂且这样吧。
没明白并且毫无帮助?那就对了。
丑陋的完整代码:Link
ps:上面给出的完整版和 Part 3 中的部分变量名不同。大家凑合凑合???

