可持久化线段树

可持久化数据结构（线段树）

Part 1 可持久化数据结构

这个世界上有众多的毒瘤数据结构，但是他们维护的大多是“数据库的最新状态”。如果想知道数据库在任意时间的历史状态（即 \(\forall i\in [1,M]\) ，执行完操作 \(i\) 后数据库的状态）。一种暴力的做法是多花费 \(M\) 倍空间，每次操作之后把整个数据结构 Copy 一遍，存储在 \(\text {hestory[i]}\) 中。但是每次修改对数据结构造成的影响可能很小，这就导致我们 Copy 了大量相同的状态，“可持久化”提供了一种思想，在每项操作结束后，仅创建数据结构中发生改变的部分的副本，不 Copy 其他部分。这样一来，维护数据结构的时间复杂度没有增加，空间复杂度仅增长为与时间同级的规模、换言之，可持久化数据结构能够高效的记录一个数据结构的所有历史状态。

Part 2 可持久化数组

有了（例题）可持久化数组，便可以实现很多衍生的可持久化功能（比如可持久化并查集）。

可持久化数组的内部实现是一棵可持久化线段树（函数式线段树）。

对于一棵普通的线段树，其树高为 \(log n\) ，如果对其单点修改，那么只有 \(logn\) 个节点发生了信息更新。对于每个被更新的节点 \(p\) ，要创建该节点的副本 \(p'\) 。只要 \(p\) 不是叶子节点，那么 \(p\) 的左右儿子中一定且最多有一个发生更新。假设发生更新的是 \(p\) 的左儿子 \(ls\) ，那么在 \(ls\) 中递归，返回时令 \(p'\) 的左儿子为新创建的副本 \(ls'\) ，右儿子和 \(p\) 的右儿子相同（因为右儿子没有发生更新），然后利用左右儿子的信息更新 \(p'\) 的信息即可。

如下图：黄色即为递归路径。原图来自这里，侵删。

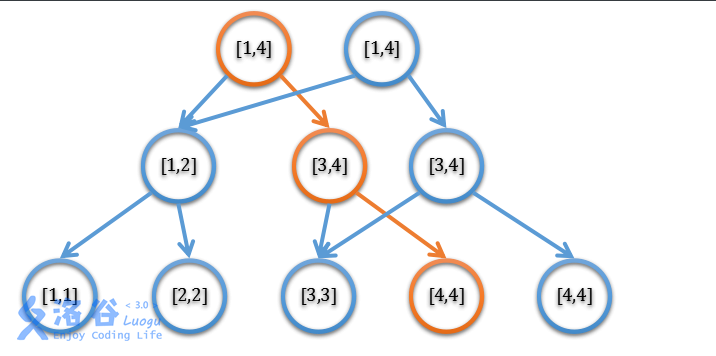
假设修改了位置 4 。从根节点开始访问，根被修改，创建副本。左儿子 [1,2] 没改，副本的左儿子设置为 [1,2] 。向右儿子 [3,4] 访问，创建副本。发现左儿子 [3,3] 没改，把副本的左儿子设置为 [3,3] 。向右儿子访问，创建副本，[4,4] 是叶子节点，无需再递归访问，于是回溯更新副本的信息。

回到例题中来，先在给出的原序列 \(A\) 上建立一棵普通的线段树。

对于每个单点修改操作，像上面叙述的一样新建一些节点，把根记录下来以便后续访问。

Code：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>

//using namespace std;

const int maxn=1000005;
#define ll long long 

inline int read(){
  int x=0,fh=1;
  char ch=getchar();
  while(!isdigit(ch)){
    if(ch=='-')
      fh=-1;
    ch=getchar();
  }
  while(isdigit(ch)){
    x=(x<<3)+(x<<1)+ch-'0';
    ch=getchar();
  }
  return x*fh;
}

int n,m,tot;
int A[maxn];

struct segment_tree{
  int value,l,r;
  segment_tree *ls,*rs;
};

struct segment_tree byte[maxn*21],*pool=byte,*root[maxn];

segment_tree* New(){
  return ++pool;
}

segment_tree* Build(const int L,const int R){
  segment_tree *u=New();
  u->l=L,u->r=R;
  if(L==R){
    u->value=A[L];
    u->ls=u->rs=NULL;
  }else{
    int mid=(L+R)>>1;
    u->ls=Build(L,mid);
    u->rs=Build(mid+1,R);
  }
  return u;
}//创建一棵普通线段树

inline bool outofrange(segment_tree* &node,const int L,const int R){
  return (node->r<L)||(R<node->l);
}

void modify(segment_tree* &pre,segment_tree* &now,const int p,const int value){
  *now=*pre;//先创建副本
  if(pre->l==p && pre->r==p){
    now->value=value;//找到位置，直接赋值
  }else{
    if(!outofrange(pre->ls,p,p)){//修改在左区间里
      now->ls=New();//给副本创建一个左儿子
      modify(pre->ls,now->ls,p,value);//继续调整
    //因为这里只要求访问，所以不用更新
    }else{//同上创建右儿子
      now->rs=New();
      modify(pre->rs,now->rs,p,value);
    }
  }
}

int query(segment_tree* &node,const int p){//正常的线段树访问
  if(node->l==p && node->r==p)
    return node->value;
  if(!outofrange(node->ls,p,p))
    return query(node->ls,p);
  else return query(node->rs,p);
}

signed main(){
  n=read(),m=read();
  for(int i=1;i<=n;++i)
    A[i]=read();
  root[0]=Build(1,n);
  for(int i=0,op,v,p,val;i<m;++i){
    v=read(),op=read(),p=read();
    if(op==1){
      val=read();
      root[++tot]=New();//新建一个根节点
      modify(root[v],root[tot],p,val);
    }else{
      printf("%d\n",query(root[v],p));
      root[++tot]=New();
      *root[tot]=*root[v];//题目要求输出后也创建一个对应版本
    }
  }
  return 0;
}

Part 3 主席树

主席树名字的由来：

第一位创造并使用这种数据结构的选手是黄嘉泰，他的名字缩写为 HJT ，所以这种数据结构本来叫 HJT 树。但是碰巧的是，当时某位共和国主席的名字缩写也是 HJT ，后来名字就渐渐变成了“主席树”......

主席树能做什么

最初版本的主席树非常 real 和 simple。它的出现只是为了解决这样一个问题：静态区间第 \(k\) 小。

解法1：线段树套平衡树

一般的静态区间第 \(k\) 小的做法是离散化之后在值域上建立权值线段树，然后线段树内再套一棵平衡树用来维护 \([L,R]\) 内数的下标。在线段树上左子节点利用平衡树查询 \(\leq r_i\) 和 \(\leq l_i-1\) 的数的个数，作差然后与 \(k\) 比较，决定递归线段树的左子树还是右子树。这种做法时间复杂度 \(O\left((N+M)log^2N\right)\)，空间复杂度 \(O(nlogn)\) 。因为平衡树支持插入删除，它可以直接支持动态区间 \(k\) 小问题，这里不再多做讨论。

解法2：主席树

先把原序列 \(A\) 离散化，离散化后 \(H[A[i]]\in [1,T]\)，然后再在 \([1,T]\) 上建立可持久化权值线段树，线段树上的每一个节点保存一个值 \(cnt\) ，表示该节点代表的值域 \([L,R]\) 内有多少个数，最初版本的 \(cnt\) 全为 0 。

扫描序列 \(A\) ，对于每个 \(A[i]\) 在可持久化线段树上对 \(H[A[i]]\) 进行单点修改，把其 \(cnt\) 值 +1 。同时，线段树内每个非叶子节点的 \(cnt\) 由左右儿子相加得到。这样，这棵可持久化线段树的第 \(i\) 个版本就维护了 \(H[A[1]]\) 到 \(H[A[i]]\) 这 \(i\) 个数的信息。

在查询区间 \([l,r]\) 的第 \(k\) 小数时，显然这个数一定来自 \([l,r]\) （废话） ，那么 \([1,l]\) 之间的数一定对答案没有影响。因为所有的版本都是来自于最初的 0 号版本，故所有的版本对值域的划分都是相同的，所以拿第 \(r\) 个版本 \([L,R]\) 区间的 \(cnt\) 减去第 \(l-1\) 个版本 \([L,R]\) 区间的 \(cnt\) 就可以得到大小在 \([L,R]\) 之间的数有几个（也就是可持久化线段树中划分相同的两个节点具有可减性）。把这个差值和 \(k\) 比较，决定递归左子树还是右子树，直到递归到某一个叶子节点时，这个差值为 \(k\) 此时这个叶子节点代表的数就是区间 \([l,r]\) 的第 \(k\) 小数。

Code：

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>

//using namespace std;

const int maxn=200005;
#define ll long long

template <typename T>
inline T const& read(T &x){
  x=0;int fh=1;
  char ch=getchar();
  while(!isdigit(ch)){
		if(ch=='-')
			fh=-1;
		ch=getchar();
	}
	while(isdigit(ch)){
		x=(x<<3)+(x<<1)+ch-'0';
		ch=getchar();
	}
  x*=fh;
  return x;
}

int n,N,m,tot;
int A[maxn],B[maxn];

void Init(){
  read(n),read(m);
  for(int i=1;i<=n;++i)
    B[i]=read(A[i]);
  std::sort(B+1,B+n+1);
  N=std::unique(B+1,B+1+n)-B-1;
  for(int i=1;i<=n;++i)
    A[i]=std::lower_bound(B+1,B+N+1,A[i])-B;
  //B[A[i]]为原值
  //A[i]为离散化值
}

struct chairman_tree{
  int l,r,cnt;
  chairman_tree *ls,*rs;
};

struct chairman_tree byte[maxn*19],*pool=byte,*root[maxn];

chairman_tree* New(){
  return ++pool;
}

inline void update(chairman_tree* &node){
  node->cnt=node->ls->cnt+node->rs->cnt;
}

inline bool outofrange(chairman_tree* &node,const int L,const int R){
  return (node->r<L)||(R<node->l);
}
//这一堆都同可持久化数组
chairman_tree* Build(const int L,const int R){
  chairman_tree *u=New();
  u->l=L,u->r=R;
  if(L==R){
    u->ls=u->rs=NULL;
    u->cnt=0;//建树时 cnt 为 0
  }else{
    int Mid=(L+R)>>1;
    u->ls=Build(L,Mid);
    u->rs=Build(Mid+1,R);
    update(u);
  }
  return u;
}

void modify(chairman_tree* &pre,chairman_tree* &now,const int p){
  *now=*pre;
  if(pre->l==p && pre->r==p){
    now->cnt++;
    return;
  }
  if(!outofrange(pre->ls,p,p)){
    now->ls=New();
    modify(pre->ls,now->ls,p);
    update(now);//回溯时更新 cnt 值
  }else{
    now->rs=New();
    modify(pre->rs,now->rs,p);
    update(now);
  }
}

//找区间 k 小相当于选 k 个最小的数，这 k 个数的最后一个就是答案
int query(chairman_tree* &Ltree,chairman_tree* &Rtree,const int k){
  if(Ltree->l==Ltree->r)//递归到叶子节点，此时一定找到 k 小
    return Ltree->l;//返回这个值
  int lcnt=Rtree->ls->cnt-Ltree->ls->cnt;
    //查询 l,r 版本左儿子中数的数量差多少
    //如果相差多于 k 个元素，那么去左儿子中选，否则去右儿子
  if(lcnt>=k) return query(Ltree->ls,Rtree->ls,k);
  else return query(Ltree->rs,Rtree->rs,k-lcnt);
    //注意递归右儿子相当于已经选了左儿子中所有的数，查询应该变为 k-lcnt
}

signed main(){
  Init();
  root[0]=Build(1,N);
  for(int i=1;i<=n;++i){
    root[++tot]=New();
    modify(root[tot-1],root[tot],A[i]);//用离散化值创建 n 个版本
  }
  for(int i=1,l,r,k;i<=m;++i){
    read(l),read(r),read(k);
    printf("%d\n",B[query(root[l-1],root[r],k)]);//查询区间 k 小
  }
  return 0;
}

写在最后

特别鸣谢：

感谢 @LSQ 耐心给我讲解关于可持久化线段树和主席树，并给出代码实现。（（并帮我 debug

本博客部分解法与定义叙述参考《算法竞赛进阶指南》，作者李煜东，特此注明。