最大异或路径

最大异或数对

在《算法竞赛进阶指南》 by 李煜东一书中，我看到了这个问题，但是某洛谷 OJ 上没有此题，（书上给出原题题号 CH1602 ，我压根不知道这个是哪个 OJ ，就放弃了 AC 原题的想法，知道原题网址的朋友可以在下方评论）所以我找到了洛谷上另一个题意相似的题目代替它。

Part 1 按位异或

按位异或有非常多的理解方式，这也导致围绕着“异或”运算的题目层出不穷，变化多端。今天先从“最大异或数对”这一题的角度，来看看异或运算的性质。另外，在下文中，\(a\) 异或 \(b\) 记作 \(a\oplus b\) 。

对于任意一个十进制 int 类型整数，它有一个自己对应的二进制表示法。假设这个数是 \(x\) ，那么它的二进制表示为 \((x)_2\) 。

例如整数 998244353 ，它的二进制表示为 \((\text{998244353})_2=00111011100000000000000000000001\) ，这里为了把它的二进制形式补全为 32 位 ( int 范围 )，在前面添加两个前导 0 。

给定另一个整数 114514 ，它的二进制表示为 \((\text{114514})_2=00000000000000011011111101010010\) 。

现在，求 \(\text{998244353} \oplus \text{114514}\) 。

进行异或运算时，先把这两个数的二进制表示“对齐”。刚才我们把这两个数的位数补到 32 位就是为了方便 “对齐” 。

对齐之后，观察对应的每一位数，若相同，则异或结果的二进制表示的这一位为 0 ，否则为 1 。

具体看下面示例：

998244353:00111011100000000000000000000001
   114514:00000000000000011011111101010010
   result:00111011100000011011111101010011
   result=998358867

再把得到结果转换为 10 进制，得到结果：\(\text{998358867}\) 。

Part 2 最大异或数对

给你包含 \(N(N\leq 2e5)\) 个 int 类型非负整数的序列 \(A\) ，最大化 \(A_i \oplus A_j\) 。

朴素的做法就是枚举每一个数，然后再枚举其他数与它异或，更新最大值，复杂度 \(O(N^2)\) 。

现在来介绍一种更快的做法：

根据上面阐述的异或运算的性质，发现两个运算数二进制下更高数位上的数不同，会导致结果更大。也就是说，这两个运算数在二进制意义下，左向右第一个不同的位置出现的越早，异或结果就越大。

更直白的，其实就是让两个数的二进制表示的公共前缀最短。处理字符串公共前缀问题，字典树 \(\text{Trie}\) 当仁不让。

先把这 \(N\) 个数都拆成二进制 01 字符串，并补全到 32 位，然后全部插入 \(\text{Trie}\) 中。

对于 \(A_i\) 对应的二进制串，在 \(\text{Trie}\) 中进行一次与检索类似的操作，尽可能往与 \(A_i\) 当前位不同字符的方向向下访问。当然了，如果与 \(A_i\) 当前位不同的指针是空的，那么只好访问与它相同的指针。如果选择了与 \(A_i\) 当前位不同的指针，记录当前位答案为 1 ，否则记录当前位答案为 0 。

如图，假设在一棵 \(\text{Trie}\) 中，插入了 2(010) , 5(101) , 7(111) 三个数，查询与 6(110) , 3(011) 异或运算结果最大的数。（为了方便画图，我们暂时使用 3 位二进制位代替 32 位二进制位）

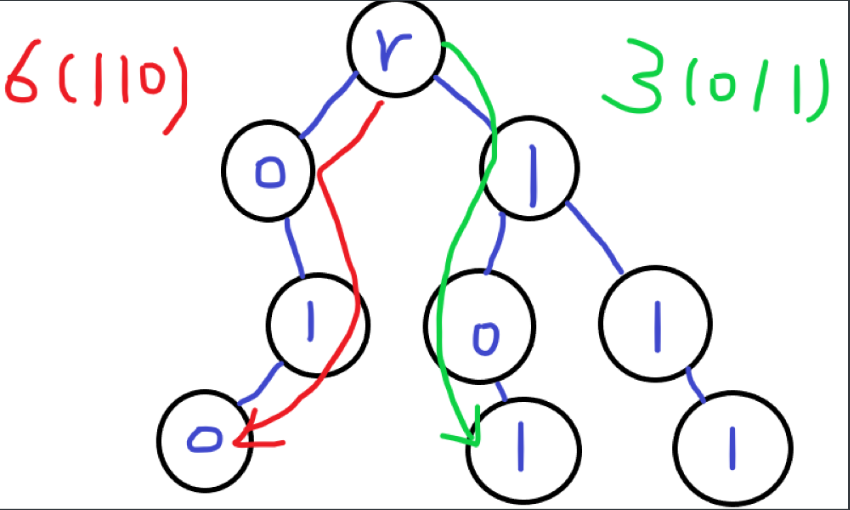
像这样，查询 6(110) 时访问路线为红色标出，查询 3(011) 时访问路线为绿色标出。答案分别为 4(100) , 6(110) 。

字典树 \(\text{Trie}\) 的插入，查询复杂度都为 \(O(L)\) ，这里字符串长度为 32 ，故 \(L=32\) 。总复杂度 \(O(NL)\) 。

Part 3 最大异或路径

题目链接

给定一棵 \(N(N\leq 1e5)\) 个节点的无根树，每个边有一个权值 \(k(0\leq k< 2^{31})\) 。从树中任意选两个点 \(x\) 和 \(y\) ，把 \(x\) 到 \(y\) 路径上的所有边权异或起来，得到的结果最大是多少？

任意选取一个点为根（假设根为 1 ），那么树上所有路径被分为两种：

1. 经过根节点的（ \(x,y\) 在根的不同子树中）
2. 不经过根节点的（ \(x,y\) 在根的相同子树中）

设 Depth[x] 表示根节点到 \(x\) 路径上所有边权的异或值，那么 Depth[x] 可以根据下式通过从根出发的 BFS 求出：

\[\text{Depth[x]=Depth[father(x)]}\oplus k \left( x,father(x) \right) \]

对于情况 1 ，直接 \(\text{Depth[x]}\oplus \text{Depth[y]}\) 得到答案。

情况 2 ，根到 \(x\) 与根到 \(y\) 的路径会有重叠部分，但是根据异或运算的性质（ \(a \oplus a =0\) ），假设把 Depth[x] 和 Depth[y] 异或起来，它们到根的路径上的重复边权异或后恰好为 0 。其实还是直接 \(\text{Depth[x]}\oplus \text{Depth[y]}\) 得到答案。

如果对于情况 2 不理解，请看下图：

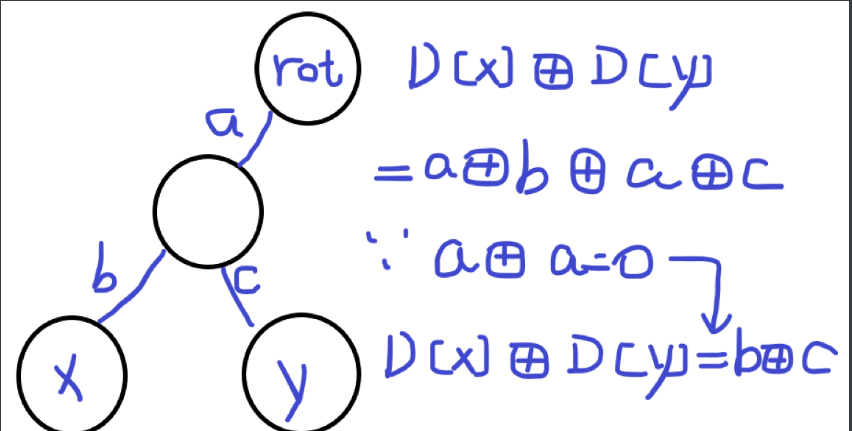
综上，问题就变成了从 Depth[1] 到 Depth[N] 中选择 2 个数，使得这两个数异或结果最大，也就是“最大异或数对”问题，可以使用 \(\text{Trie}\) 在 $O(NL) $ 的复杂度内求解。

代码：

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>

//using namespace std;

inline int read(){
	int fh=1,x=0;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')
			fh=-1;
		ch=getchar();
	}
	while('0'<=ch&&ch<='9'){
		x=(x<<3)+(x<<1)+ch-'0';
		ch=getchar();
	}
	return fh*x;
}

const int maxn=100005;

struct Trie{//01Trie
  int tag;
  Trie *s[2];
  Trie(){
    tag=0;
    s[0]=s[1]=NULL;
  }
};

struct Trie *root;//root is an empty node

Trie* New(){
  Trie *node=new Trie;
  //按道理来说应该使用内存池而不是new，因为new速度慢
  //但是在使用内存池时，我一发精妙空间计算后MLE了，索性改成new，这样不用计算内存池大小了
  node->s[0]=node->s[1]=NULL;
  return node;
}

void Insert(const int *str,const int len){
  Trie *p=root;
  for(int i=0;i<len;++i){
    if(p->s[str[i]]==NULL)
      p->s[str[i]]=New();
    p=p->s[str[i]];
  }
  p->tag++;
}

int Get_maxxor(const int *str,const int len){
  Trie *p=root;
  int ans[50],it=0,sum=0;
  for(int i=0;i<len;++i){//尝试向不同数字方向访问
    if(p->s[str[i]^1]==NULL)
      p=p->s[str[i]],ans[it++]=0;
    else p=p->s[str[i]^1],ans[it++]=1;
  }
  for(int i=0,j=it-1;i<32;++i,--j)//还原答案为10进制
    sum+=ans[i]*pow(2,j);
  return sum;
}

int n;
int D[maxn],visit[maxn];
std::vector< std::pair<int,int> >v[maxn];

void bfs(const int s){//预处理Depth数组
  std::queue<int>Q;
  Q.push(s);
  visit[s]=1;
  D[s]=0;
  while(Q.size()){
    int x=Q.front();
    Q.pop();
    for(int i=0;i<v[x].size();++i){
      int y=v[x][i].first;
      if(visit[y]) continue;
      Q.push(y);
      visit[y]=1;
      D[y]=D[x]^v[x][i].second;
    }
  }
}

int turn[35];
inline void Turn(int x){//改为32位2进制数
  memset(turn,0,sizeof turn);
  int i=31;
  while(x){
    if(x&1) turn[i--]=1;
    else turn[i--]=0;
    x>>=1;
  }
}

signed main(){
  root=New();
  n=read();
  for(int i=1,x,y,z;i<=n-1;++i){
    x=read(),y=read(),z=read();
    v[x].push_back(std::make_pair(y,z));
    v[y].push_back(std::make_pair(x,z));
  }
  bfs(1);
  for(int i=1;i<=n;++i){
    Turn(D[i]);
    Insert(turn,32);
  }
  int ans=0;
  for(int i=1;i<=n;++i){
    Turn(D[i]);
    ans=std::max(ans,Get_maxxor(turn,32));
  }
  printf("%d\n",ans);
  return 0;
}

本博客部分证明、例题参考了《算法竞赛进阶指南》，作者李煜东，特此注明。