最近公共祖先
Part 1:了解LCA
\(LCA\)(Least Common Ancestors),中文翻译是“最近公共祖先”
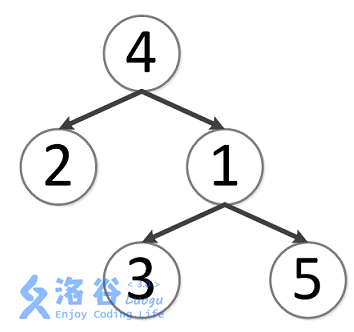
(原图来自洛谷)
对于给定的一棵树和这棵树的树根(如上图)
给定两个节点,他们的最近公共祖先(以下简称\(LCA\))就是这两个点分别到树根的简单路径中经过的所有点的交集中,深度最深的一个
以上面的图为例子,点对\((3,5)\)的\(LCA\),我们按照定义来求:
\(step 1\):求出\(3\)到树根的路径是\(3 \rightarrow 1 \rightarrow 4\)
\(step 2\):求出\(5\)到树根的路径是\(5 \rightarrow 1 \rightarrow 4\)
所以点对\((3,5)\)的\(LCA\)就是点\(1\)
Part 2:\(LCA\)的求法
\(LCA\)的定义很好理解,相信大家很容易就明白了,现在我们讨论怎么求两个节点的\(LCA\)
法一:向上标记法
向上标记法是最简单的求\(LCA\)的暴力算法
算法主要思路:对于两个给定节点\((a,b)\),我们任意挑选一个,这里我们假设选择\(a\)节点
\(step 1:\)从\(a\)节点到树根一个一个节点的遍历,对遍历到的节点进行标记
\(step 2:\)从\(b\)节点到树根一个一个节点的遍历,如果遍历到一个被标记的节点,那么这个点就是点对\((a,b)\)的\(LCA\)
向上标记法既是按照定义求\(LCA\)——求出简单路径交集的最深节点
但是这是一个赤裸裸的暴力,它的复杂度是\(O(n)\),其中\(n\)是点的深度
但是对于一棵比较高大威猛的树来说,仅仅线性的复杂度显然不够优秀,所以代码就不再给出了,我们考虑优化
法二:倍增求\(LCA\)
还是考虑给定一棵树和根节点,求树上点对\((a,b)\)的\(LCA\)
上面的算法慢的主要原因是每次仅仅向上标记\(1\)个节点,那么我们想到了倍增算法,每次向上跳\(2^k\)个点
如果想实现这个算法,我们就得记录每个点向上\(2^k\)步的父节点,我们可以用如下的预处理方式解决
预处理:记录各个点的深度和他们\(2^i\)级的的祖先,用数组\(\rm{depth}\)表示每个节点的深度,\(fa[i][j]\)表示节点\(i\)的\(2^j\) 级祖先。
\(LCA\) \(prework\) \(code:\)
void dfs(int now, int fath) { //now表示当前节点,fath表示它的父亲节点
fa[now][0] = fath; depth[now] = depth[fath] + 1;
for(int i = 1; i <= lg[depth[now]]; ++i)
fa[now][i] = fa[fa[now][i-1]][i-1];
//这个转移可以说是算法的核心之一
//意思是now的2^i祖先等于now的2^(i-1)祖先的2^(i-1)祖先
//原理显而易见,根据初中数学,可以得到这个式子:2^i = 2^(i-1) + 2^(i-1)
for(int i = head[now]; i; i = e[i].nex)
if(e[i].t != fath) dfs(e[i].t, now);
}
然后是怎么倍增的问题,如果我们拿到点对\((a,b)\)就直接开始向上跳的话,由于初始时\(a,b\)的深度不一样,这样使得跳跃步数难以控制,增大了思维量(其实几乎不可做。
为了解决这个问题,我们考虑先把\(a,b\)中深的那一个跳到浅的那一个同一深度,然后一起向上倍增跳跃,这样我们对于边界条件的处理会方便许多
调整深度也很简单,我们假设\(a\)的深度大于\(b\)的深度,那么先把\(a\)向上跳\(2^k\)步,如果到达的深度比\(b\)浅,那么尝试跳\(2^{k-1}\)步,以此类推,直到跳到与\(b\)的深度相等
调整完了,下面是倍增求\(LCA\)的步骤
\(step 1:\)把\(a,b\)调整到同一深度的祖先后,如果这两个点相同,说明其中深度浅的是\(LCA\),如果不同,执行\(2\)
\(step 2:\)如果他们的\(2^k\)祖先是同一个点,说明跳多了,我们就“反悔”,看看\(2^{k-1}\)是不是同一个点,如果不是同一个点,就向上跳\(2^{k-1}\)步
\(step 3:\)重复\(2\),直到跳到某一个深度,此时\(a\)和\(b\)的父节点重合了,那么这个父节点就是所求\(LCA\)
倍增求\(LCA\)核心代码:
inline int LCA(int x, int y) {
for(int i=1; i<=n; i++){
lg[i]=lg[i-1];
if(i==1<<lg[i-1])lg[i]++;
}//预处理一下2^k,小小的常数优化
if(depth[x] < depth[y]) //用数学语言来说就是:不妨设x的深度 >= y的深度
swap(x, y);
while(depth[x] > depth[y])
x = fa[x][lg[depth[x]-depth[y]] - 1]; //先跳到同一深度,方便处理
if(x == y) //如果x是y的祖先,那他们的LCA肯定就是x了
return x;
for(int k = lg[depth[x]] - 1; k >= 0; --k)
if(fa[x][k] != fa[y][k]) //因为我们要跳到它们LCA的下面一层,所以它们肯定不相等,如果不相等就跳过去。
x = fa[x][k], y = fa[y][k];
return fa[x][0]; //返回父节点
}
这样查询一次\(LCA\)的复杂度是\(O(logn)\),其中\(n\)是点的深度,比向上标记法快了不少
剩下的建树就不用讲了吧,用邻接表然后把上面的代码\(copy\)一下直接调用\(LCA()\)函数即可
2020/8/22 update
更新了一下,因为觉得上面的那个方法虽然常数小,但是对初次接触\(LCA\)的童鞋不太友好,因为要预处理东西的太多了
这里给出一个常数比较大但是好写易懂一点的做法:
首先,还是要预处理父子关系,但是在\(dfs\)里我们只处理一个节点的父亲是谁,不再倍增处理
然后我们的\(dfs\)就会简化成这个样子:
void dfs(const int x){
vis[x]=true;//标记已经遍历过这个节点
for(int i=0;i<v[x].size();i++){//扫描这个边的所有儿子,这里v是vector邻接表
int y=v[x][i];//儿子是y
if(vis[y]) continue;//如果y已经访问过了,continue掉
dep[y]=dep[x]+1;//儿子的深度比父亲大1
fa[y][0]=x;//儿子的2^0祖先是他的父亲
dfs(y);//递归预处理
}
}
\(dfs\)里只预处理了每个节点的\(2^0\)级祖先,然后我们在调用完\(dfs\)预处理之后,在主函数里暴力倍增预处理:
for(int i=1;i<=20;i++)//枚举2的1-20次方
for(int j=1;j<=n;j++)//枚举每个点
fa[j][i]=fa[fa[j][i-1]][i-1];//同上,一个点的2^i祖先等于他的2^(i-1)祖先的2^(i-1)祖先
然后,用来常数优化的\(lg\)数组也不要了,在\(LCA()\)里也暴力处理:
inline int LCA(int x,int y){
if(dep[x]>dep[y]) std::swap(x,y);
for(int i=20;i>=0;i--)//枚举跳2^20到2^0步,暴力的向上跳到与x相同的位置
if(dep[fa[y][i]]>=dep[x])
y=fa[y][i];
if(y==x) return x;
for(int i=20;i>=0;i--)//枚举一起跳2^20到2^0步,暴力向上爬树
if(fa[x][i]!=fa[y][i]){
x=fa[x][i];
y=fa[y][i];
}
return fa[x][0];//返回最后的父节点就是LCA
}
下面是完整的代码,看起来非常的简洁清爽(代价就是常数大
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<algorithm>
#include<set>
#include<map>
#include<utility>
#include<iostream>
#include<list>
#include<ctime>
#include<cmath>
#include<cstdlib>
#include<iomanip>
typedef long long int ll;
inline int read(){
int fh=1,x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-') fh=-1;ch=getchar(); }
while('0'<=ch&&ch<='9'){ x=(x<<3)+(x<<1)+ch-'0';ch=getchar(); }
return fh*x;
}
inline int _abs(const int x){ return x>=0?x:-x; }
inline int _max(const int x,const int y){ return x>=y?x:y; }
inline int _min(const int x,const int y){ return x<=y?x:y; }
inline int _gcd(const int x,const int y){ return y?_gcd(y,x%y):x; }
inline int _lcm(const int x,const int y){ return x*y/_gcd(x,y); }
const int maxn=500005;
const int inf=0x3f3f3f3f;
int n,rot,q;
std::vector<int>v[maxn];
int fa[maxn][25],dep[maxn];
bool vis[maxn];
void dfs(const int x){
vis[x]=true;
for(int i=0;i<v[x].size();i++){
int y=v[x][i];
if(vis[y]) continue;
dep[y]=dep[x]+1;
fa[y][0]=x;
dfs(y);
}
}
inline int LCA(int x,int y){
if(dep[x]>dep[y]) std::swap(x,y);
for(int i=20;i>=0;i--)
if(dep[fa[y][i]]>=dep[x])
y=fa[y][i];
if(y==x) return x;
for(int i=20;i>=0;i--)
if(fa[x][i]!=fa[y][i]){
x=fa[x][i];
y=fa[y][i];
}
return fa[x][0];
}
int main(){
n=read(),q=read(),rot=read();//n个点,q次询问,根为rot
for(int i=1,x,y;i<=n-1;i++){
x=read(),y=read();
v[x].push_back(y);
v[y].push_back(x);
}
dep[rot]=1;//根节点深度为1,不然LCA调整深度时会出错
dfs(rot);//根是rot
for(int i=1;i<=20;i++)
for(int j=1;j<=n;j++)
fa[j][i]=fa[fa[j][i-1]][i-1];
for(int i=0,x,y;i<q;i++){
x=read(),y=read();//查询x,y的LCA
printf("%d\n",LCA(x,y));
}
return 0;
}
上面简化版的做法具体慢多少?
在同样的评测环境(无\(O_2\)下),\(n、q\leq500000\)的数据,优化常数的版本\(10\)个测试点一共跑了\(1.03s\),而暴力简化版跑了\(2.13s\)
所以大概要慢一半以上,这里还是建议写常数小的版本啦\(qwq\)
法三:\(RMQ\)(Range Minimum/Maximum Query)求LCA
算法原理
其实,这种做法算的上是一个奇技淫巧吧
先普及一个小知识点:欧拉序(怎么又是欧拉

(其实我尝试过自己画图但是真的太丑了所以还是用洛谷的图叭
欧拉序,其实和深度优先遍历序(先序遍历)非常的相似:
为了方便大家理解,我们先写出这棵树的\(dfs\)序:\(4,2,1,3,5\)
那么我先写出欧拉序,然后再解释:\(4,2,4,1,3,1,5,1,4\)
大家可能已经看出来了,欧拉序其实就是\(dfs\)序在回溯时又重新记录了一下遍历的点而已
现在给出这样一张图:
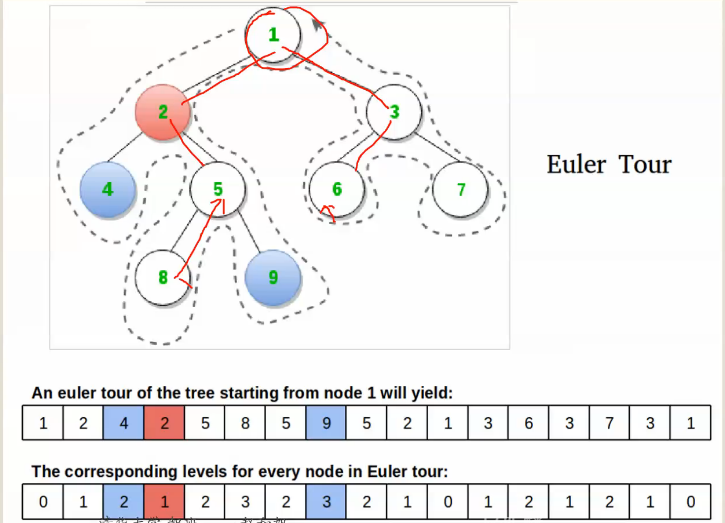
图中给出了一棵以\(1\)为根的树,下面的第一个序列是欧拉序,第二行是欧拉序中各点在树中的深度(深度序)
我们发现一个有趣的现象——我们查询\(x,y\)的\(LCA\)其实就是在深度序中\(x\)的下标和\(y\)的下标之间的最小值的下标在欧拉序中所对应的节点
如果上面的语言描述不够简洁,我们用严格的数学语言描述一遍:
\(1、\)找到查询点\(x,y\)在欧拉序中找到这两个点第一次出现的下标,记作\(l,r\)。
\(2、\)在深度序上对区间\([l,r]\)上查询最小值,记下标为\(qwq\)
\(3、\)那么\(x,y\)的\(LCA\)就是欧拉序中下标为\(qwq\)的点
是不是很玄学奇妙,又比倍增\(LCA\)更加易于理解呢?
这个算法的核心原理在于:对于欧拉序遍历,任意一棵非空子树的根节点一定在其所有儿子节点的前面和后面各出现一次,而根节点的深度一定比儿子节点的深度浅,那么两个点之间出现的深度最小值就是这棵子树的根节点,也就是包含\(x,y\)最小子树的根节点,同时也是他们的\(LCA\)
预处理
\(1、\)欧拉序当然要先预处理啦!同时为了保证珂爱的复杂度不被破坏,我们还要记录第\(i\)个点在欧拉序中的下标,这样我们单点查询欧拉序下标的时候就是\(O(1)\)而不是遍历的\(O(n)\)
\(2、\)深度序,表示第\(i\)个点在\(dfs\)中的层数,这个可以在求欧拉序的时候顺便求出来
预处理\(Code\):
void dfs(const int x,const int depth){
vis[x]=1;//标记一下已经走过x号节点
dis[id]=depth;//id是迭代器,depth为当前深度
eula[id][0]=x;//记录欧拉序
if(eula[x][1]==0) eula[x][1]=id;//这一维代表第i个点的欧拉序下标
id++;//完成记录后迭代器++
for(unsigned int i=0;i<v[x].size();i++)//因为懒,所以用的vector存图
if(vis[v[x][i]]==0){//如果没有被访问过
dfs(v[x][i],depth+1);//递归遍历就好
dis[id]=depth;//再记录一遍
eula[id][0]=x;//再记录一遍
id++;//完成记录后迭代器++
}
}
下面的问题将变成一个赤裸裸的\(RMQ\)问题,对于\(RMQ\)问题我们有一大堆优秀的算法,比如\(st\)表,线段树……等等都是优秀的\(RMQ\)算法
由于弱,我选择了使用建树和查询都是\(log\)级且自带大常数的线段树来求\(RMQ\)
求出了\(RMQ\)之后,我们把这个下标对应到欧拉序中,输出即可
蒟蒻代码展示:
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<algorithm>
#include<set>
#include<map>
#include<utility>
#include<iostream>
#include<list>
#include<ctime>
#include<cmath>
#include<cstdlib>
inline int read(){
int fh=1,x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-') fh=-1;ch=getchar(); }
while('0'<=ch&&ch<='9'){ x=(x<<3)+(x<<1)+ch-'0';ch=getchar(); }
return fh*x;
}
inline int _abs(const int x){ return x>=0?x:-x; }
inline int _max(const int x,const int y){ return x>=y?x:y; }
inline int _min(const int x,const int y){ return x<=y?x:y; }
//以上全是缺省源,无视即可,另外自己写几个很简单的函数可以优化常数哦
const int maxn=500005;
std::vector<int>v[maxn];//vector代替了邻接表建图
int n,m,s,vis[maxn],dis[maxn*4],eula[maxn*4][2],id=1;
std::pair<int,int>querynum;//第一维记录下标,第二维记录最小值,用于更新
//eula[i][1]是第i个点的欧拉遍历下标,eula[][0]是欧拉遍历序
//dis[i]第i个点的深度
void dfs(const int x,const int depth){
vis[x]=1;
dis[id]=depth;
eula[id][0]=x;
if(eula[x][1]==0) eula[x][1]=id;
id++,vistimes++;
for(unsigned int i=0;i<v[x].size();i++){
if(vis[v[x][i]]==0){
dfs(v[x][i],depth+1);
dis[id]=depth;
eula[id][0]=x;
id++;
}
}
}//上面有注释了
struct seg{//线段树的结构体,使用指针建树比*2,*2+1建树方法省下一半空间,强烈安利
int l,r,v,num;//l,r是这个区间的左右端点,v是区间最小值,num,最小值下标,和最小值一起维护
seg *ls,*rs;//左儿子指针,右儿子指针
inline bool in_range(const int L,const int R){ return (L<=l)&&(r<=R); }//判断是否是子集
inline bool outof_range(const int L,const int R){ return (R<l)||(r<L); }//判断是否无交集
inline void push_up(){
v=_min(ls->v,rs->v);//区间最小值=左儿子最小值和右儿子最小值取min
num=(ls->v<=rs->v)?(ls->num):(rs->num);//维护最小值下标
}
int query(const int L,const int R){
if(in_range(L,R)){
if(v<querynum.second){//区间最小值<已知最小值
querynum.first=num;//记录下标
querynum.second=v;//更新已知最小值
}
return v;//是查询区间的子集,返回区间最小值
}
if(outof_range(L,R)) return 0x3f3f3f3f;//与查询区间无交集,返回极大值
return _min(ls->query(L,R),rs->query(L,R));//递归查询最小值,维护更新下标
}
};
seg byte[maxn*4],*pool=byte;//使用内存池建立线段树
seg* New(const int L,const int R){
seg *u=pool++;
u->l=L,u->r=R;
if(L==R){
u->v=dis[L];
u->num=L;
u->ls=u->rs=NULL;
}else{
int Mid=(L+R)>>1;
u->ls=New(L,Mid);
u->rs=New(Mid+1,R);
u->push_up();
}
return u;
}
int main(){
n=read(),m=read(),s=read();
for(int i=1,x,y;i<=n-1;i++){
x=read(),y=read();
v[x].push_back(y);
v[y].push_back(x);
}//建立邻接表
dfs(s,0);//预处理欧拉序和深度序
seg *rot=New(1,id-1);//建树
for(int i=1,x,y;i<=m;i++){
querynum.first=0;//用来记录最小值下标
querynum.second=0x3f3f3f3f;//用来更新最小值,所以先赋值极大
x=read(),y=read();//读入查询点
int l=eula[x][1],r=eula[y][1];//查询这两个点的下标
if(l>r) std::swap(l,r);//如果l>r,交换,因为线段树不支持查询l>r的情况
int qwq=rot->query(l,r);//查询区间最小值下标
printf("%d\n",eula[querynum.first][0]);//输出这个下标在欧拉序中的对应节点
}
return 0;
}
好了,今天关于\(LCA\)算法的分享就到这里了(跪求三连

