深度优先搜索（dfs）与出题感想

在3月23号的广度优先搜索（bfs）博客里，我有提到写一篇深搜博客，今天来把这个坑填上。

第一部分：深度优先搜索（dfs）

以上来自百度百科。

简单来说，深度优先搜索算法就是——穷举法，即枚举所有情况，找寻可能的解法。

问题一：如何穷举？

假设我们对于1~4这些连续的自然数，我们需要求他的全排列。（不能用STL函数啊喂！！！）

显然，我们要做出3次选择：

第一步，我们需要从1~4这4个数里选出一个，作为全排列的第一个数，然后标记他（假设我们选择1）。

第二步，我们需要从剩下没标记的3个数中选出一个，作为第二个数，标记他（假设选择2）。

第三步，选择3，第四步，选择4。

这时我们回过头来，看看已经选过的数（1 2 3 4），发现在第3次选择中，我们可以选择其他的数。

显然在第3次选择中，我们除了3，还可以选择4，这样我们的三个选择就是（1 2 4）第四次可以选择3。这样就是（1 2 4 3）。

再回头看，第二次选择中，我们除了2，还可以选择3或4，假设我们选择3，这时我们的数列是（1 3），重做第三次对于两个数的选择，这时生成两个排列（1 3 2 4）和（1 3 4 2）。

如此再回到第一次选择，选2，选3，选4……直到枚举结束，我们就获得了1~4的全排列。

我们把我抽象的描述转化成这样一颗搜索树，就变得形象了：

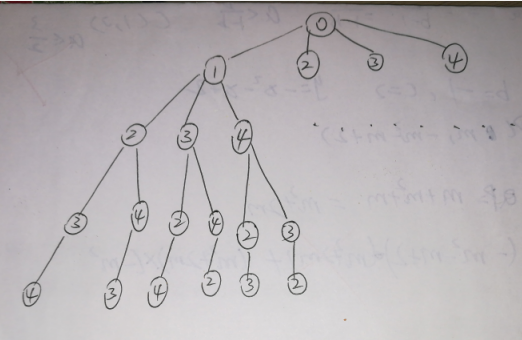
我们对全排列的搜索就像上图的树一样。（从0开始第一次有4个选择，第二次有3个选择，第三次有2个选择，第四次有一个选择，到第四次，搜索结束）

其实就像初中的统计概率的题目一样画树状图。。。

问题二：知道如何穷举了，那么dfs是怎样的一种穷举方法？

很简单，对于一个图来说：

我们首先访问一个节点v，对与v节点相连的所有节点进行检索，检索到第一个之后（假设叫v2），对v2这个节点相连的（除了v）所有节点检索……

直到检索到vn这个节点，再没有新节点与他相连，这时，回到vn-1，检索除了vn-2和vn有没有别的节点与他相连，如果有，对该点进行检索。

如此反复，直到整个图的所有节点（也就是所有状态）都被访问过了，搜索算法结束。

还是上图帮助理解：

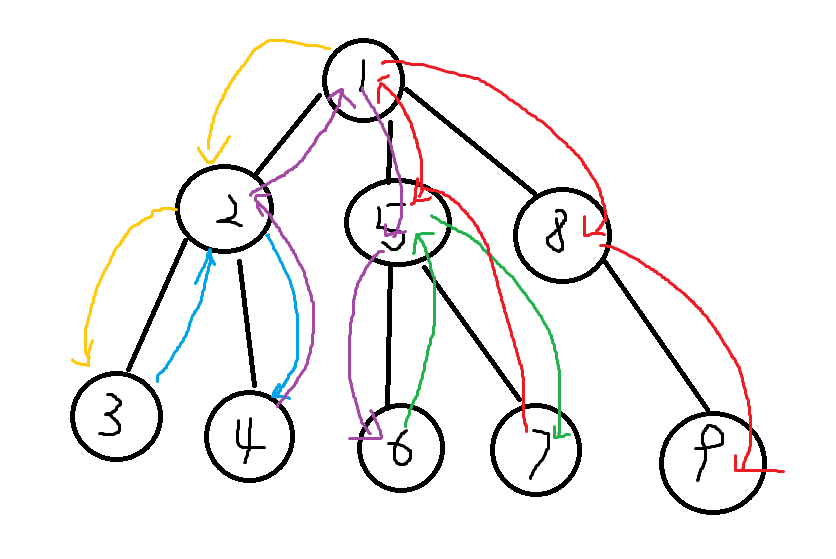
黄色：第一次搜索，返回枚举情况。（1 2 3）

蓝色：返回并进行第二次搜索，返回枚举情况。（1 2 4）

紫色：返回并进行第三次搜索，返回枚举情况。（1 5 6）

绿色：返回并进行第四次搜索，返回枚举情况。（1 6 7）

红色：返回并进行第五次搜索，返回枚举情况。（1 8 9）

至此，对整个图的遍历结束。

你可以认为dfs是优先对一个节点的所有儿子节点进行遍历，直到找到一个没有儿子节点的节点，即完成一次枚举，他如此重复直到完成对整个图的遍历。

 Part 2：深度优先搜索代码实现

我们先看看几个例题来熟悉一下dfs的代码

洛谷P1644

 

 

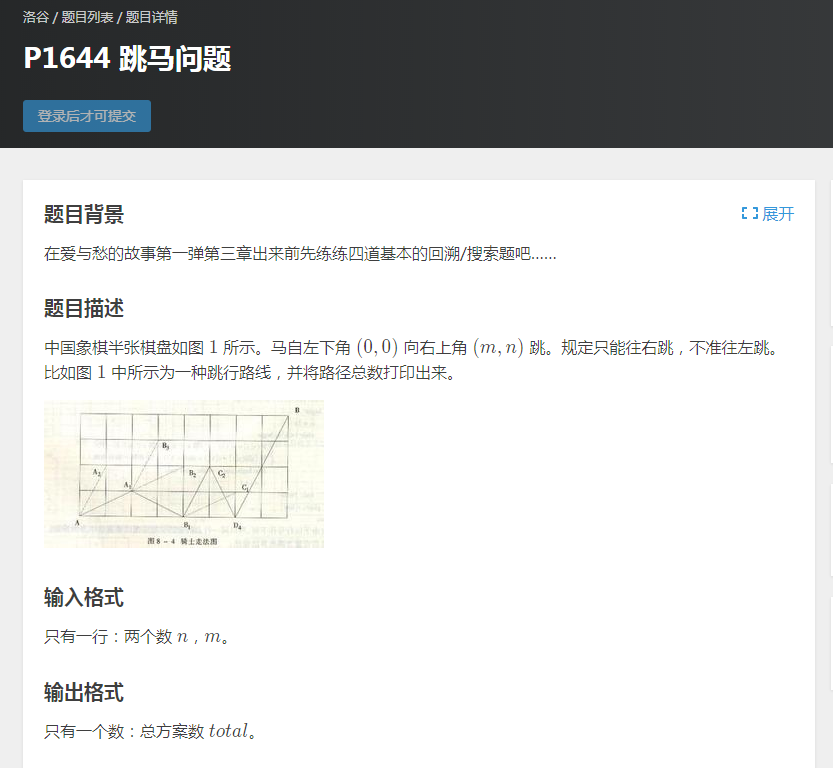
很经典的一道深度优先搜索的题目，下面我来说说具体思路：

本题我们可爱的马只能向右边跳，所以降低了很大的复杂度，dfs可以轻松AC本题。

我们需要枚举所有可能的路径，（即马向4个方向走，直到无法再走一步）然后判断这条路走到最后是不是合法的，如果合法，方案总数+1，然后回溯，如果不合法，直接回溯即可。

看看代码（我尽量给注释）

//P1644
//#include<zhangtao.std>
//zhangtao AK IOI 
#include<iostream>
using namespace std;
int go[5][2]={{0,0},{-1,2},{-2,1},{1,2},{2,1}};//初始化马的四个方向 
int mapp[20][20];//小地图 
int m,n,way;
void dfs(int x,int y)
{
    if(x==0&&y==n)
    {
        way++;//如果到达终点，路径总数++ 
        return;
    }
    mapp[x][y]=1;//标记已经走过的点 
    for(int i=1;i<=4;i++)
    {
        if(x+go[i][0]<0||x+go[i][0]>m||y+go[i][1]<0||y+go[i][1]>n)
        {
            continue;
        }
        if(mapp[x+go[i][0]][y+go[i][1]]==1)
        {
            continue;
        }//这两句都是判断被搜到的点是否合法 
        dfs(x+go[i][0],y+go[i][1]);//合法，dfs之！ 
        mapp[x+go[i][0]][y+go[i][1]]=0;//回溯(重新标记为0) 
    }
}
int main()
{
    cin>>m>>n;
    dfs(m,0);
    cout<<way;
    return 0;//调用函数解决问题即可！ 
}

具体做法代码里已经详细解释了，这里我重点讲一下回溯。

什么是回溯？

很简单，当我们搜到终点，或者是一个不合法的结果的时候，就要进行回溯，继续对别的点进行搜索。

不同于树，在地图中搜索，我们可能有好几种方法搜到同一个点。

我们上一次搜过一个点之后，再尝试别的方法，如果这个点没有被重新标记为没有走过，我们的程序就不会对它进行搜索，导致枚举总数不够，这也是回溯的必要性。

那么，怎么回溯？

首先看我们的dfs函数，它的特性是它是一个递归函数，就是自己嵌套自己，所以说，我们的程序执行起来大概是这样的：

第一次进行dfs的时候，进行第一次for循环，搜到了第一个点，进入第二层dfs，第二次for，第三层dfs……

假设我们进行到了第n次dfs，没有找到合法的点，这时就要回溯了。

注意，我们在进行到第n次dfs时，上面的第n-1个for循环并没有执行完，所以我们只需要在进行完第n次dfs之后，把所有变量还原到第n-1次的时候的大小，程序自动回到第n-1次for的时候，就可以再次使用这些变量而不受第n次搜索的影响。具体操作也很简单，下面是伪代码：

dfs(x+go[i][0],y+go[i][1]);//合法，dfs函数下方是回溯区域
mapp[x+go[i][0]][y+go[i][1]]=0;//在dfs下面都是回溯区，你可以不止对一个变量进行回溯，可以是多个，你想回溯几个就回溯几个！

Part 3：我成为毒瘤出题人之后的一些感想与该题题解

众所周知，洛谷不光满足OIer们刷题的需求，我们甚至可以和同学或者小伙伴们互相出题来做做，一起进步，所以我就尝试性的出了一个题。（正好教练鼓励过我们自己出几个题）

但是同学们直呼毒瘤！！！

我们先看看这个题，这是网址https://www.luogu.com.cn/problem/U115344

 

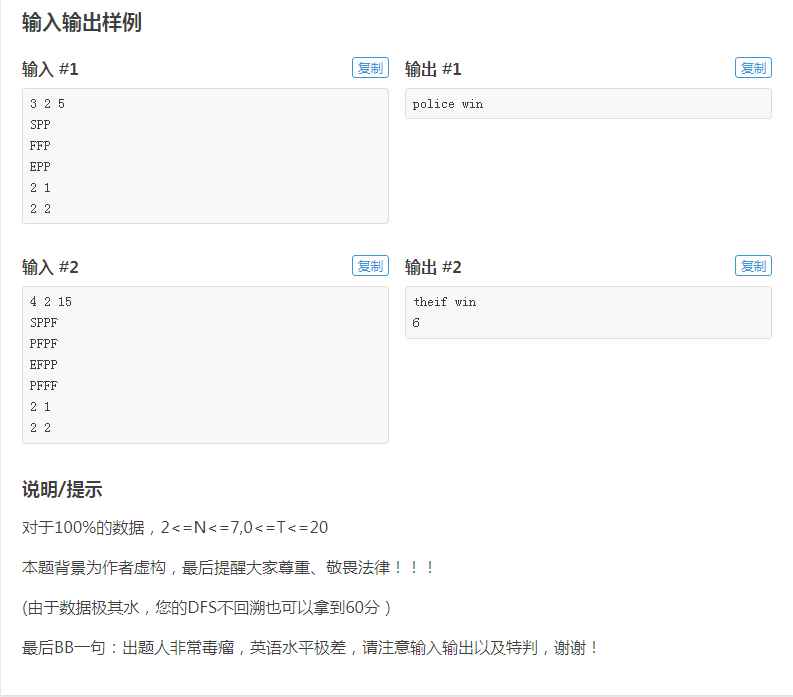
 我们先来看看这个题我故意埋的一个坑，可以注意到：输出样例中的theif win 和thief win（小偷获胜）的英文并不一样，有些没有注意到的同学就会被卡掉。

其次，由于题目数据比较小，所以我对时间复杂度和空间复杂度的要求提高了很多（截图中没有），我改成了100ms时间限制，1MB内存限制。

（这不是很毒瘤吧……）

不多BB，我们把它当做一个例题来讲：

首先，我们要初始化小地图，题目中给出的S是出发点，E是终点，这两个点需要标记好。P是漂移点，需要进行标记，F的话看您个人喜好，不标记也没啥事。

初始化被警察拦住的点。

之后，我们从出发点进行dfs，这次我们有时间限制，搜索树的高度限制为T+1，我们再开一个参数，如果这个参数比T要大，我们需要return。

走到P点，漂移数要+1，回溯时要-1，当前搜索高度（时间）-1。

如果搜到终点，比较搜到终点已经进行的漂移数，如果比之前的大，更新这个值。

最后，输出最大值即可。（这很简单嘛！）

//逮虾户De jaVu
//#include<zhangtao.std>
#include<iostream>
using namespace std;
int mapp[15][15];
char dd[15][15];
int go[5][2]={{0,0},{1,0},{-1,0},{0,1},{0,-1}};
int N,M,T,sx,sy,ex,ey,way,a,b,flag;
void dfs(int x,int y,int t,int drift)//x，y为坐标，t为时间，drift为已经进行的漂移数 
{
    if(t>T) return;//超出时间，return 
    if(x==ex&&y==ey)
    {
        if(drift>way)
        {
            way=drift;//更新最大值 
        }
        flag=1;//搜到终点，flag=1 
        return;
    }
    mapp[x][y]=1;//标记已经走过 
    for(int i=1;i<=4;i++)
    {
        if(N<x+go[i][0]||x+go[i][0]<=0||N<y+go[i][1]||y+go[i][1]<=0) continue;
        if(mapp[x+go[i][0]][y+go[i][1]]==1) continue;//判断是否合法 
        t++;
        if(dd[x+go[i][0]][y+go[i][1]]=='P') drift++;
        dfs(x+go[i][0],y+go[i][1],t,drift);
        mapp[x+go[i][0]][y+go[i][1]]=0;//回溯区，路径标记为0 
        t--;//时间-1 
        if(dd[x+go[i][0]][y+go[i][1]]=='P') drift--;//如果走过的点是P，漂移数-1 
    }
}
int main()
{
    cin>>N>>M>>T;
    for(int i=1;i<=N;i++)
    {
        for(int j=1;j<=N;j++)
        {
            cin>>dd[i][j];
            if(dd[i][j]=='S')
            {
                sx=i;
                sy=j;
            }
            if(dd[i][j]=='E')
            {
                ex=i;
                ey=j;
            }//记录起始点和终点，初始化 
        }
    }
    for(int i=1;i<=M;i++)
    {
        cin>>a>>b;
        mapp[a][b]=1;//记录路障点 
    }
    if(ex==0&&ey==0)
    {
        cout<<"police win";
        return 0;//特判终点是否被路障标记 
    }
    dfs(sx,sy,0,0);//进行搜索 
    if(flag==0) cout<<"police win";//没搜到终点，输出答案 
    else cout<<"theif win"<<endl<<way;//搜到终点，输出方案数 
    return 0;
}

代码注释已经很详细了，相信各位可以看懂，那么今天的分享就到这里了，希望我的分享能让大家对dfs算法有更深的理解！

老规矩——祝大家，身（少）体（掉）健（头）康（发）。