比较基础的广度优先搜索算法!!!
公告:在2020/3/24 0:20之前把最短路模板拿走的同志们,看这里!
如果你回来了请仔细阅读公告!
真的对不起大家!是我误人子弟了,我在2020/3/24 0:20前发布的博客所给出的最短路模板是错误的。
因为我是临时拿一个一维的广搜改的,所以好多地方数组都是写的一维的,没有改过来。
在之前的拿走模板的同志们真的抱歉了。我以后一定检查好自己的文章再发布,不再犯这样的错误了
广度优先搜索算法的定义!!!
憋了四天了,本蒟蒻终于学会了广搜,即刻与大家分享学习经历!
先上广搜的定义!
宽度优先搜索算法(又称广度优先搜索)是最简便的图论的搜索算法之一,这一算法也是很多重要的图论算法的原型。
Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。
其别名又叫BFS,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。
换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
——来自百度百科
个人的理解
百度百科的解释一塌糊涂,上面说的好多知识我也不会,怕各位弄不明白,(瞎JB操心)就写一个我个人对广搜的理解。
广度优先搜索算法,与深度优先搜索算法不同的是,他从一个节点出发,会优先遍历这一个点的所有子节点,
然后再从这个点的第一个子节点遍历所有子节点,再是第二个……第三个……(废话)
下面举个栗子:
就像一个庞大的家族,我们要查家族中某个人的户口,就先从祖宗查起,先找祖宗有几个孩子。
如果你要找的人不是祖宗的孩子,那就从老大的第一个孩子……第二个孩子……,老二的第一个孩子……第二个孩子,
一直循环往复,一定可以返回一个值(你要查的那个人)。
既然名字那么像,广搜和深搜各自有什么特点和不同呢?
其实这俩哥们虽然都叫搜索,但是实现方法完全不同,深搜是依靠递归,广搜是依靠队列。
这也导致了双方特点和应用上的不同。
深搜呢,最大的优势就是——不!占!空!间!
写起来也简单,深搜有回溯算法,如果在这一棵子树中没有得到结果,就去另一棵。
深搜被广泛用于限定条件求方法种数的问题,比如八皇后问题,显然广搜对每个节点只遍历一次的方法是不能解决问题的。
深搜也有很明显的缺点,容易TLE,大家每次写暴力的时候都会与这个TLE作斗争,运行效率低也是深搜的一大短板。
广搜呢,优势在于寻找最短路!
广搜与深搜不同的是,整张图的每个子节点都只会被搜到一次,每个节点总是以最短路径的形式被访问。
所以广搜对于寻找最短路来说有奇效。
因为广搜对于每个子节点只会搜索一次,所以程序运行效率也会提升。(当然深搜可以优化复杂度,比如记忆化、完全剪枝这些,不多BB)
缺点也很明显,因为广搜依赖队列,如果子节点太多,会爆系统栈,所以可能会MLE。
对于某一些问题,深搜和广搜都能胜任。
因为都是枚举所有可能,所以这两个都只适用于数据规模较小的情况。
广搜怎么实现呢?
我的上一篇博客已经提到了队列,广搜就是依靠队列来实现。
具体请看图:这是具体的思路了

广搜的应用之一——寻找最短路。
找最短路是一类模板感特别强的题,所以套模板可以应付大多数的最短路问题!!!(一个蒟蒻瞎比比啥)
下面我提供一个最短路模板,不一定是最好的,仅供参考。
#include<iostream> #include<queue>//STL队列头文件 using namespace std; int mapp[110][110];//小地图,记录路径用 int step[110][110];//记录步数用的 int go[5][2]{{0,0},{1,0},{-1,0},{0,1},{0,-1}};//定义可以走的方向 struct STU{//定义一个结构体,包括横纵坐标 int xx; int yy; }; queue<STU>q;//定义一个结构体类型的队列 int n,m,sx,sy,ex,ey,qx,qy,tx,ty;//n,m是题目要求的地图边界 //我个人建议固定自己喜欢的变量名,建立模板化的体系,这样写最短路的时候会更加井井有条! int bfs(int x,int y)//x,y是初始结点 { q.push((STU){x,y});//坐标入队 mapp[x][y]=1;//标记路径已经走过 while(q.size()!=0)//当队列不为空的时候,说明还没遍历完 { qx=q.front().xx;//qx,qy为当前坐标 qy=q.front().yy; q.pop();//弹出初始坐标,进行对该坐标的搜索 if(qx==ex&&qy==ey)//如果qx,qy的数值满足终止条件,停止搜索并返回值 { return step[qx][qy];//返回计步数组的值 } for(int i=1;i<=4;i++)//枚举方向(对于可以向左右的数轴问题,对于别的你可以看情况枚举路径可能) { tx=qx+go[i][0];//go是方向数组,tx,ty是向这个方向走后的坐标 ty=qy+go[i][1]; if(1>tx||tx>m||1>ty||ty>n)//我个人习惯,地图是从(1,1)开始 { continue; } if(mapp[tx][ty]==1)//如果超出边界或者已经被搜过,即视为不合法,continue掉 { continue; } step[tx][ty]=step[qx][qy]+1;//如果合法,计步数组的值为上一步+1 mapp[tx][ty]=1;//记录路径,避免重复搜索 q.push((STU){tx,ty});//把tx,ty入队 } } return -1;//如果没搜到结果,返回-1 }
核心就是while里的弹出,判断和入队操作。
如果您们如果觉得广搜难,可以慢慢体会。简单的题目前只有求最短路非用广搜不可。其他深搜都可以胜任(如果您深搜也不太会的话,我如果过几天闲的没事会更新深搜博客,大概吧)
到了后期,广搜就很重要了,图论算法的常客。所以一定要扎实!(瞎操心*2)
行了,理论知识都齐备了,下面看看几个最短路的题(都是一本通上的)
真题实战
ybt1249(该题可以深搜替代!!!)
(因为之前复制题目的时候出了点bug,这里放图片)
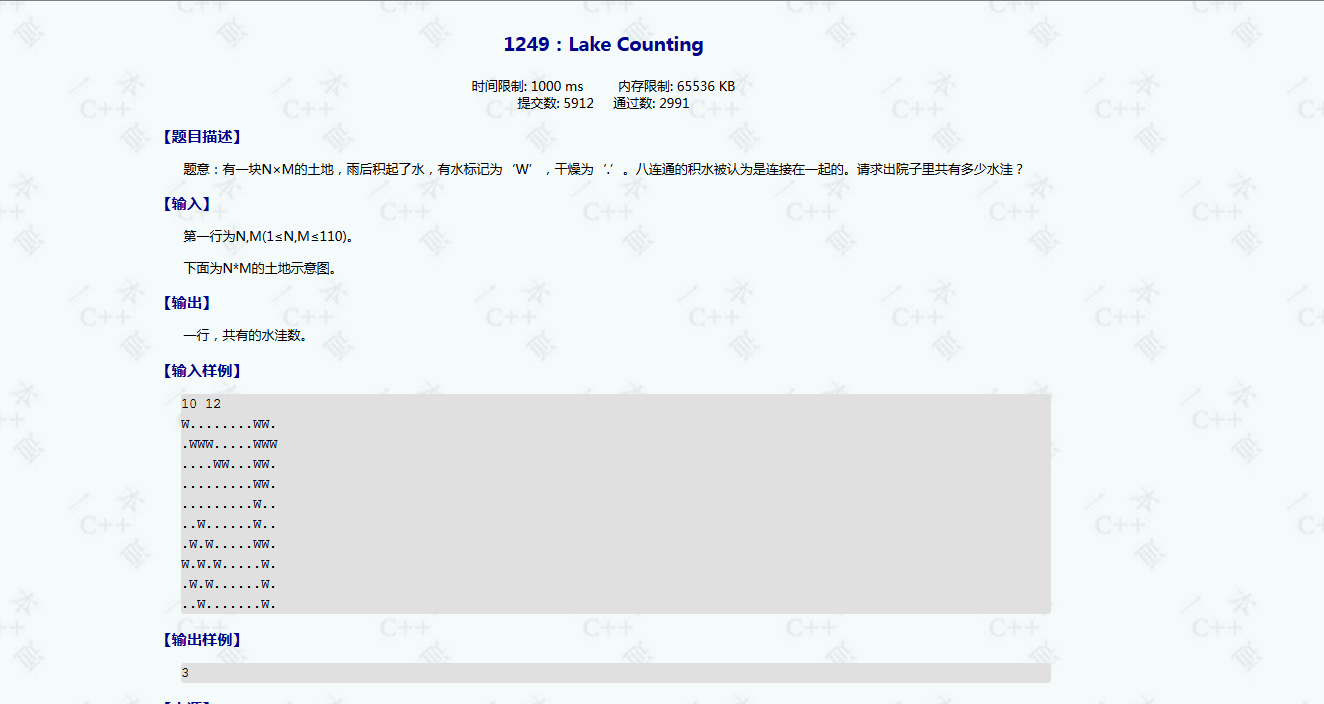
我先来BB两句思路!
首先,题目中说W是水坑,然后每一个水坑的八个方向中如果有另一个水坑,就视为一个大水坑。
最后问给出的矩阵中有几个水坑。
这个题和那个细胞的例题大同小异。
我们要for嵌套循环一遍整个图,找到一个W点就开始一次广搜,把和他连在一起的W变成句号
这样会把一个水坑完全变成旱地,实现了统计个数的操作。
上代码!
//1249 #include<iostream> #include<queue> using namespace std; char dd[115][115];//字符数组,用来读入 int mapp[115][115]; int go[9][2]{{0,0},{1,1},{1,0},{1,-1},{0,1},{0,-1},{-1,1},{-1,0},{-1,-1}}; struct STU{ int xx; int yy; }; int m,n,qx,qy,tx,ty,ans; queue<STU>q; void bfs(int x,int y) { q.push((STU){x,y}); mapp[x][y]=0;//把初始的点变成0 while(q.size()!=0) { qx=q.front().xx; qy=q.front().yy; q.pop(); for(int i=1;i<=8;i++) { tx=qx+go[i][0]; ty=qy+go[i][1]; if(tx<1||tx>n||ty<1||ty>m) { continue; } if(mapp[tx][ty]==0) { continue; } mapp[tx][ty]=0;//搜到的1变成0 q.push((STU){tx,ty});//全都是模板操作 } } } int main() { cin>>n>>m; for(int i=1;i<=n;i++)//这里变成1和0是我个人喜欢,因为我字符串渣一个 { for(int j=1;j<=m;j++) { cin>>dd[i][j]; if(dd[i][j]=='W') { mapp[i][j]=1;//读入数据,如果输入W,变为1 } } } for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { if(mapp[i][j]==1)//如果是1,开始搜索 { ans++;//答案+1 bfs(i,j); } } } cout<<ans; return 0; }
这是这道题的写法,看下一类(最短路问题)
ybt1254
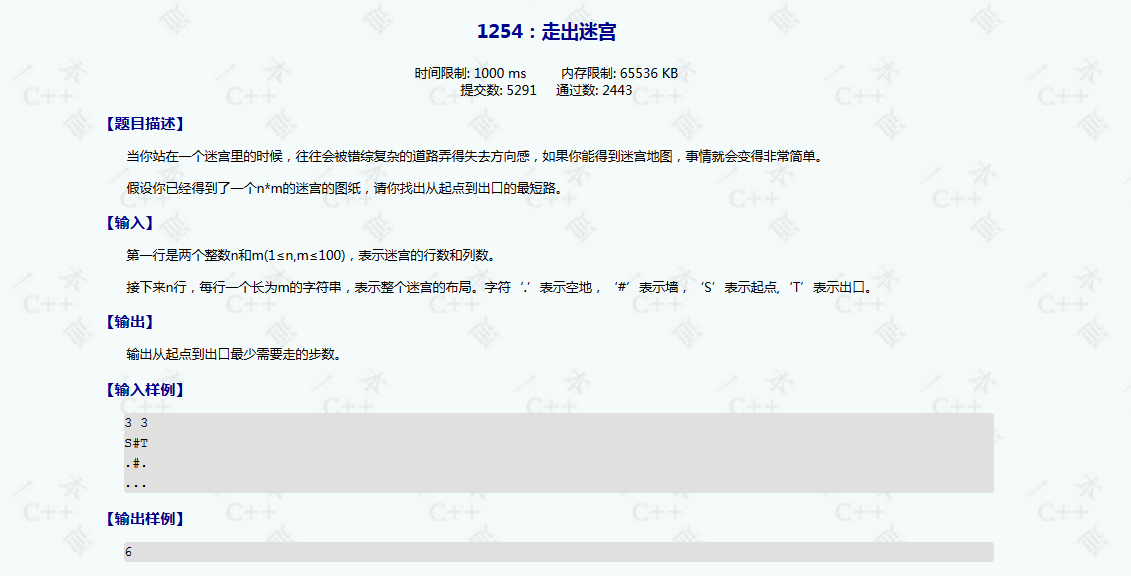
非常经典的最短路问题,可以用广搜解决!
上代码!
//1254 #include<iostream> #include<queue> using namespace std; char dd[110][110]; int mapp[110][110]; int step[110][110]; int go[5][2]{{0,0},{1,0},{-1,0},{0,1},{0,-1}}; struct STU{ int xx; int yy; }; queue<STU>q; int n,m,sx,sy,ex,ey,qx,qy,tx,ty; int bfs(int x,int y) { q.push((STU){x,y}); mapp[x][y]=1; while(q.size()!=0) { qx=q.front().xx; qy=q.front().yy; q.pop(); if(qx==ex&&qy==ey) { return step[ex][ey]; } for(int i=1;i<=4;i++) { tx=qx+go[i][0]; ty=qy+go[i][1]; if(tx<1||tx>m||ty<1||ty>n) { continue; } if(mapp[tx][ty]==1) { continue; } mapp[tx][ty]=1; step[tx][ty]=step[qx][qy]+1; q.push((STU){tx,ty});//以上模板操作,变量名都没换,不需要注释 } } } int main() { cin>>m>>n; for(int i=1;i<=m;i++)//这个操作是记录障碍,起点和终点 { for(int j=1;j<=n;j++) { cin>>dd[i][j]; if(dd[i][j]=='S') { sx=i; sy=j; } if(dd[i][j]=='#') { mapp[i][j]=1; } if(dd[i][j]=='T') { ex=i; ey=j; } } } cout<<bfs(sx,sy);//输出广搜返回的值 return 0; }
最短路问题到这就说的差不多了,大家应该也都找到门道了。
只要套模板,再稍微处理一下主程序就好了。
然而,我做题的时候踩了一个大坑,卡了我好长时间,我花了一个小时才搞明白,跟大家分享一下,希望大家不会像我这个蒟蒻一样踩坑叭。
(这里BB一句,还有一个小细节:起数组名的时候,不要和函数库里的函数同名,不然本地跑没事,交到评测网站上会显示CE,比如time,map等等)
ybt1256
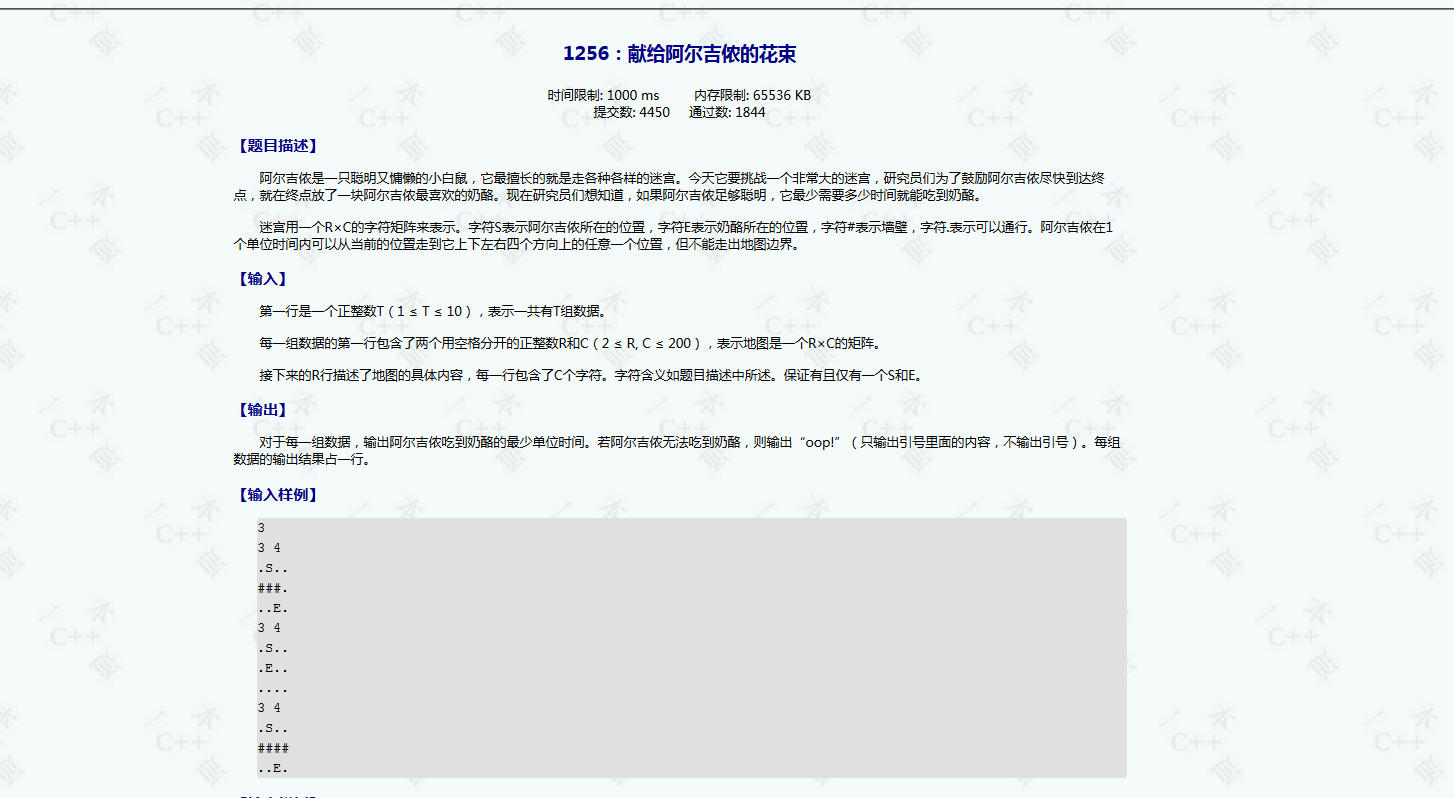
这个题也是最短路问题,唯一不同的是他有多组输入数据,所以在进行一次广搜之后需要注意:
清空你的数组和队列!!!
如果没有清空,你的队列里可能会有一些上次搜索的遗物,
数组里可能还记录着上次的路径和步数!!
我就是这么被卡的,然后知道我的队列没清空之后,用了一个错误的方法清队列,导致没清干净,还是WA。
上AC代码(我太难了)
//1256 #include<iostream> #include<cstdio> #include<cstring> #include<queue> using namespace std; char dd[210][210]; int mapp[210][210]; int step[210][210]; int go[5][2]={{0,0},{1,0},{-1,0},{0,1},{0,-1}}; struct STU{ int xx; int yy; }; queue<STU>q; int T,m,n,sx,sy,ex,ey,qx,qy,tx,ty,ans,big; int bfs(int x,int y) { q.push((STU){x,y}); mapp[x][y]=1; while(q.size()!=0) { qx=q.front().xx; qy=q.front().yy; q.pop(); if(qx==ex&&qy==ey) { return step[ex][ey]; } for(int i=1;i<=4;i++) { tx=qx+go[i][0]; ty=qy+go[i][1]; if(tx<1||tx>m||ty<1||ty>n) { continue; } if(mapp[tx][ty]==1) { continue; } mapp[tx][ty]=1; step[tx][ty]=step[qx][qy]+1; q.push((STU){tx,ty});//以上模板操作,不BB } } return -1;//如果不行,返回-1 } int main() { cin>>T; for(int i=1;i<=T;i++) { cin>>m>>n; for(int j=1;j<=m;j++)//地图记录到mapp数组中 { for(int k=1;k<=n;k++) { cin>>dd[j][k]; if(dd[j][k]=='S') { sx=j; sy=k; } if(dd[j][k]=='E') { ex=j; ey=k; } if(dd[j][k]=='#') { mapp[j][k]=1; } } } ans=bfs(sx,sy);//ans记录广搜的返回值,如果返回-1,说明没搜到结果,输出oop! if(ans!=-1) { cout<<ans<<endl;//返回答案 } else { cout<<"oop!"<<endl; } memset(mapp,0,sizeof(mapp));//清空数组 memset(step,0,sizeof(step)); big=q.size();//就是这里卡的我!这里必须用一个变量记录队列大小,不能放到for的终止条件里 for(int l=0;l<big;l++)//如果q.size()放到终止条件里,它会随着你弹出元素改变大小,导致不能清空队列 { q.pop();//如果没清空队列,里面会有奇怪的东西,干扰结果 } m=0,n=0,sx=0,sy=0,ex=0,ey=0,qx=0,qy=0,tx=0,ty=0,ans=0;//无视就好了,当时确实是被卡着急了,写了个这个 } return 0; }
我再多说一句:
(如果您是while用户,可以写while(q.size!=0)q.pop();)并且我上面说的您可以无视。
我再重申一遍,有多组数据的时候记得清空你的数组和队列!!!
好了,今天的学习分享就到这里,喜欢的别忘了一键三连!!!


