6.赫夫曼树与赫夫曼编码

实验6-赫夫曼树与赫夫曼编码

实验目的

• 掌握赫夫曼树的构成造算法与实现；
• 掌握赫夫曼编码的构成及实现。

说明

• 参考代码里面使用 char[] 保存赫夫曼编码，倒着存，再复制到新的 char[]里面，太繁琐了，改用 string 代替了

代码

#include <iostream>
#include <limits.h>	 // UINT_MAX
#include <string>	 // std::string
#include <algorithm> // std::reverse

using std::cin;
using std::cout;
using std::endl;
using std::reverse;
using std::string;

//赫夫曼树定义
struct HTNode
{
	unsigned int weight;
	unsigned int parent, lchild, rchild;
};

typedef HTNode *HuffmanTree;

typedef string *HuffmanCode; // 存储赫夫曼编码， 用string方便

// 返回 i 个结点中权值最小的树的根结点序号，后面函数 select( )调用
int min(HuffmanTree HT, int i)
{
	int flag;
	unsigned int weight = UINT_MAX; // 一开始假设权值很大(输入的权值不可能比这个更大)
	// 从头开始找权值最小的、没有父节点的结点(parent==0)
	for (int j = 1; j <= i; j++)
		if (HT[j].weight < weight && HT[j].parent == 0)
		{
			weight = HT[j].weight; // 记录当前结点的权值
			flag = j;
		}
	HT[flag].parent = 1; //给选中的根结点的双亲赋 1，避免第 2 次查找该结点
	return flag;
}

//在 i 个结点中选择 2 个权值最小的树的根结点序号
void Select(HuffmanTree HT, int i, int &s1, int &s2)
{
	s1 = min(HT, i); //最小结点序号
	s2 = min(HT, i); //次小结点序号
}

//构造赫夫曼树 HT
void CreatHuffmanTree(HuffmanTree &HT, int n)
{
	int m, s1, s2, i;
	if (n <= 1)
		return;
	m = 2 * n - 1;			 // n 个结点需要 2n-1个存储单元
	HT = new HTNode[m + 1];	 //0 号单元未用，所以需要动态分配 m+1 个单元
	for (i = 1; i <= m; ++i) //将 1~m 号单元中的双亲、左孩子，右孩子的下标都初始化为 0
	{
		HT[i].parent = 0;
		HT[i].lchild = 0;
		HT[i].rchild = 0;
	}
	cout << "请输入叶子结点的权值: ";
	for (i = 1; i <= n; ++i)
		cin >> HT[i].weight;
	// 从第一个空位置开始，每次合并之前的两个权值最小的结点，构造哈夫曼树
	for (i = n + 1; i <= m; ++i)
	{
		Select(HT, i - 1, s1, s2);					  // 从当前位置之前找到两个权值最小的结点
		HT[s1].parent = HT[s2].parent = i;			  // 把它们合并, 当前位置就是合并后的新结点
		HT[i].weight = HT[s1].weight + HT[s2].weight; //合并后的结点的权值是两个两个子节点的和
		HT[i].lchild = s1;							  // 左孩子结点是小的这个
		HT[i].rchild = s2;
	}
}

//从叶子到根逆向求每个字符的赫夫曼编码
void CreatHuffmanCode(HuffmanTree &HT, HuffmanCode &HC, int n)
{
	int this_node, this_parent; // 当前结点序号, 当前结点的父节点序号
	HC = new string[n + 1];		// 0 号位置不用
	for (int i = 1; i <= n; i++)
	{
		this_node = i;
		this_parent = HT[this_node].parent;
		while (this_parent != 0) // 父节点不为 0 说明有父节点, 有就一路跟上去
		{
			if (HT[this_parent].lchild == this_node) // 当前结点是左孩子
				HC[i] += "0";						 // 编码字符串加个 0
			else
				HC[i] += "1"; // 右孩子则加个 1

			this_node = this_parent; // 当前结点指向父节点, 一路跟进，直到根节点
			this_parent = HT[this_node].parent;
		}
		reverse(HC[i].begin(), HC[i].end()); // 把字符串翻转过来(从叶子往根遍历上去的, 所以得到的编码是反的)
	}
}

//显示赫夫曼编码值
void Show(HuffmanTree &HT, HuffmanCode &HC, int n)
{
	for (int i = 1; i <= n; i++)
	{
		cout << "结点权值: " << HT[i].weight << "\t编码:" << HC[i] << endl;
	}
}

int main()
{
	HuffmanTree HT;
	HuffmanCode HC;
	int n;
	cout << "请输入叶子结点的个数: ";
	cin >> n;
	CreatHuffmanTree(HT, n);
	CreatHuffmanCode(HT, HC, n);
	Show(HT, HC, n); //输出编码
}

运行截图

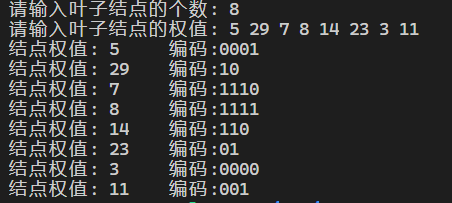
OOP 版

还没写。。。