一，专著研读（第三章-数据预处理）

一，专著研读（第三章-数据预处理）

• 数据预处理的主要任务
  主要步骤：数据清理---数据集成---数据规约---数据变换
  
• 数据清理
  缺失值处理（忽略元组，人工填充，全局常量填充，中心值填充，同一类中值填充，概率最大的值填充）
  噪声和离群点
  噪声（分箱法，回归方法平滑数据）
  离群点分析（通过聚类检测离群点，剔除离群点）
  
• 数据集成
  合并来自多个存储的数据，解决冗余和不一致问题等等。
  卡方检验
  统计样本的实际观测值预理论推断值之间的偏离程度。偏离程度决定卡方值的大小，值越大越不符合，值越小，偏差越小，趋于符合，为零完全符合
  标称数据的卡方检验
  数值数据的相关系数和协方差
  \(X^{2}=\sum_{i=1}^{I}\sum_{j=1}^{J}\frac{\left ( O_{ij}-E_{ij} \right )^{2}}{E_{ij}}\)
  对于数值数据，计算属性A,B相关系数，估计这两个属性的相关度rA,B，两个属性的相关度在-1和1之间，rA,B大于零则A，B是正相关的。pearson系数是用协方差的值/标准差的乘积
  \(r_{A,B}=\frac{\sum_{i=1}^{n}\left ( a_{i-\bar{A}} \right )\left ( b_{i-\bar{B}}  \right )}{n\sigma _{A}\sigma _{B}}=\frac{\sum_{i=1}^{n}\left ( a_{i}b_{i} \right )-n\bar{A}\bar{B}}{n\sigma _{A}\sigma _{B}}\)
  数值数据的协方差
  \(Cov\left ( A,B \right )=E\left ( \left ( A-\bar{A} \right )\left ( B-\bar{B} \right ) \right )=\frac{\sum_{i=1}^{n}\left ( a_{i}-\bar{A} \right )\left ( b_{i}-\bar{B} \right )}{n}\)
• 数据规约
  主要目的是得到数据的简化版，仍能起到同样的作用。方法有三种：维规约，数量规约，数据压缩。
  PCA
  用协方差矩阵计算特征向量降低维度，假设原始数据为M元素N特征(MXN)，则特征矩阵为（NXK），计算出（MXK）
  过程
  将数据标准化，数据排列成N行M列的矩阵A，求A的协方差矩阵C；
  求C的特征值和特征向量，即主成分；
  排列主成分（由大到小），选择前K行组成特征矩阵P(KXN)；
  结果矩阵B=PA，B(KXM);
  第一个新坐标轴的选择是原始数据中方差最大的方向，第二个新坐标轴的选择是与第一个新坐标轴正交且方差次大的方向，重复此过程（坐标轴正交，重复原始数据的所有特征维数）。
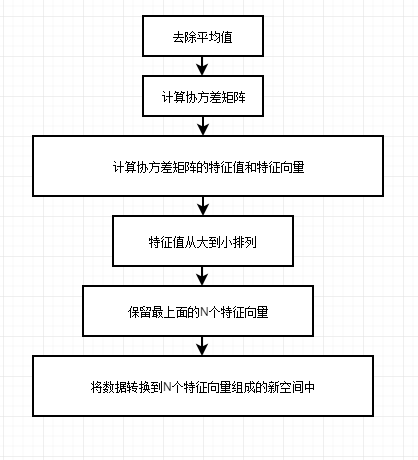
  如何得到包含最大差异性的主成分方向：
  计算数据矩阵的协方差矩阵的特征值及特征向量，选择特征值最大（包含方差最大）的N个特征所对应的特征向量组成的矩阵。
  

DWT（小波变换）

将向量X变换成不同的数值小波系数向量X`，是一种很好的有损压缩，和傅里叶变换（DFT）有关系，比傅里叶提供与原始数据更接近的近似数据。有待进一步学习理解。