算法基础番外:原码反码与补码
前言
位运算这东西其实我一直都是能避免就避免,但是前一段时间老师上课突然讲了一个位运算的用法,而今天刚好又在算法课上学到了位运算(算法课上没有深究,只是讲了两个用法),所以我想着干脆直接借着这次机会把这方面搞得全面一点一劳永逸得了,所以我查了大量的资料,也大概总结出来了一些知识。
这篇属于是番外篇了,并不是课上的内容,单纯是我出于好奇自己搜资料总结的知识点,所以单独列出来,位运算属于课程本篇,所以我会写在另一篇博客里,将两者区分出来。
正文
原码,反码与补码
原码
原码是最基本的一种数据方式,我们拿最常见的8位二进制数来举例。
原码的定义主要就是为了引入符号位这一概念
对于原码来说,第一位是符号位,0代表正,1代表负。而后面的7位则用来记录数据的二进制
比如对于19来说,原码为
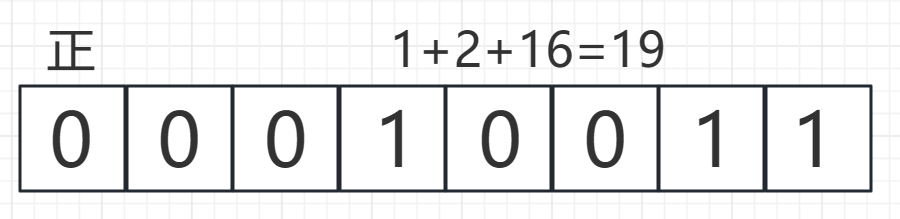
对于-19来说,原码为
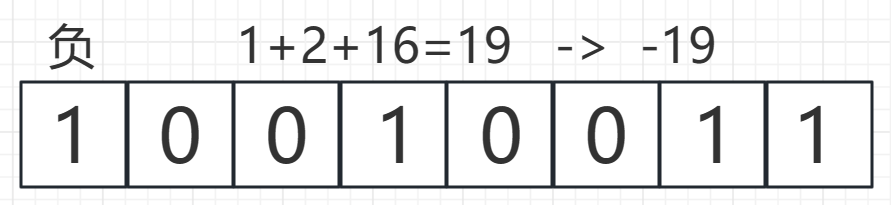
所以对于8位二进制数来说,我们也可以求出他的数值范围。由于有一位用来记录符号而非数值,所以实际有效位数为7,那么对于正号/负号来说就可以存放2^7=128个数,其中两边各有二进制表示为0(00000000与10000000),所以实际数值范围为[-127 , 127]
上面我们说两边各有一个0,其实分别为+0与-0,这就产生了二义性问题,这个我们后面再讲
反码
实际上,在计算器的数字电路中只有加法器,没有所谓的”减法器“,这是因为前人发现减法都可以转化为加法,所以没有必要再额外设计一个减法器。
对于a-b,我们都可以转换为a+(-b),然而如果我们使用原码进行这样的运算就会出现问题:比如2的原码为00000010,-2的原码为10000010,两者相加结果为10000100,也就是-4,这是错误的,所以我们需要改变一些规则来使我们的这种减法转换为加法的思想在实际运用中成立。
经过数学家的推导(我不会,所以不细讲),发现如果让正数的原码保持不变,让负数的原码除了符号位余下的所有位取反(1变0,0变1),就可以实现了,至于为什么可能就比较高深了。在进行反码的运算时,与原码不同,反码的符号位是要与数值一起参与运算的。
需要注意的是,如果我们采用了反码,那么运算完得到的结果也是反码,如果我们想计算出结果的十进制答案,就需要将这个反码转换为原码(只有负数需要转换,正数的原码反码一样所以不需要)。
虽然原码也能表示出负数,但是并不符合a - b = a + (-b)这个基本数学规律,所以其实原码的负数并不是真正意义上的。因此,部分文章中才会说反码的作用相当于数学中的负数,这是因为他符合了基本数学规律,是真正的负数。
由于负数反码是由正数原码通过取反得出来的,而正数原码的取值范围是[0 , 128],所以反码的最终取值范围是[-127 , 127]。
原码与反码的问题
上面我们在计算取值范围的时候就会发现,正数与负数中都会存在一个二进制去代表0。对于原码来说是00000000与10000000。对于反码来说是00000000与11111111。
这样的话数值0就会产生二义性。一个数值有两种编码方式对于计算机来说是不合理的,所以我们需要进一步调整来解决这个问题。
补码
为了解决上述问题,就有人想到了让正数不变,让负数区间从[-127 , 0]移动至[-128 , -1],也就是集体向后移动一位。
举一个例子:-3的反码为11111100,-4的反码为11111011。那么根据上面的思想,我们就应该让11111100来代表-4,这种移动后的表示方法我们成为补码(可以理解为对反码打了个补丁)。
所以我们得出对于-4来说,反码为11111011,补码为11111100,这里我们就发现了规律,一个数的补码=反码+1 。求一个十进制数的补码流程为:得出原码,取反得到反码(符号位不去反),反码+1
反码的11111111表示0,现在我进行补码转化,也就是让他加1,那么他就会变成100000000,这显然是超过我们8位二进制的范围的(他是9位),我们则直接省略进位的1,也就是当作00000000来处理,而这也是正数0的补码(正数的原码,反码,补码相同),我们就成功将正0和负0的二进制表示结果转化为一个式子了。
原理再深入:”模“
现在我们再来浅显的研究一下其中的数学原理。
模,在计算器里叫做MOD,在C语言中我们使用%来进行取模运算。而此处模”是指一个计量系统的计数范围。如时钟等。计算机也可以看成一个计量机器,它也有一个计量范围,即都存在一个“模”。
以时钟为例,加入现在是9点,我们想让时针回退四,其实有两种方法:
- 将时钟往回拨4,也就是一种减法
- 将时钟往前拨,把这一圈走完后再让时针指向5,这是在”模“体系中的加法
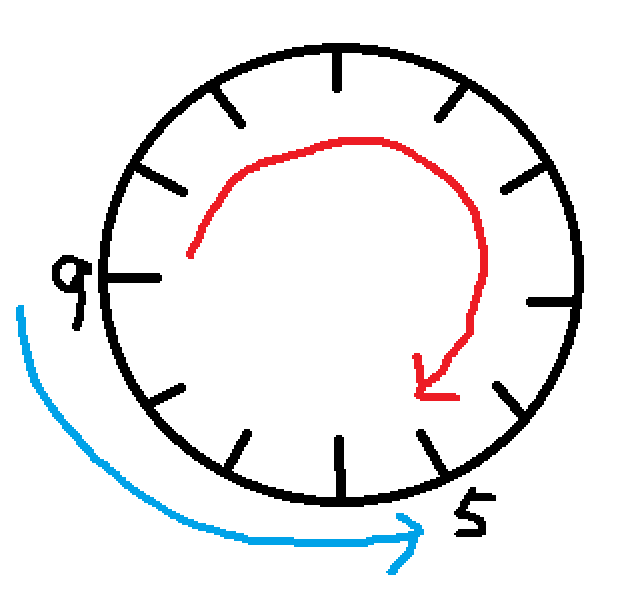
我们再引入一个概念同余数:如果a和b满足a%c == b%c那么我们就称a和b是同余数。
现在我们就可以大致理解出反码是怎么想出来的了:我们认为我们的8位二进制是一个模,那么下面这个例子:
2-1=2+(-1) = [0000 0010]原+ [1000 0001]原= [0000 0010]反+ [1111 1110]反
如果我们先暂时认为1111 1110是一个原码,那么他代表的其实是126 。那么就变成了2 + 126 = 128,现在由于我们把二进制认为是一个模,也就是127作为钟表的12点,那么很明显,128代表的其实是1 。而这正是这个计算式的正确答案。
所以我们就能初步理解反码从何而来了,其实就是将负数转化为正数,而这个正数是取值范围内的最大值。
我们先讨论a与b为正值,a-b >0的情况,对于8位二进制可以写出等式a-b = a+(127-b) = 127+(a-b),由于a-b >0,所以一定会利用到模的性质,所以a+(127-b) = [127+(a-b)]%127 = 127%127+(a-b)%127 = a-b 。所以反码的目的就是将a-b变为a+(127-b),而正好如果将负数原码m除去符号位全部取反,我们得到的数就是我们需要的最大正同余数n的原码(我不会证明),我们把这个最大正同余数m的原码称为n的反码。
同样的对于补码这种分析也成立,由于补码+1,所以我们这里认为模是128而不是127,然后再经过上述分析,依然成立。我们认为补码每128刻度为一轮,也就是[-128 , 128],只不过由于0的特殊性所以128无法表示。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号