汉诺塔I && II
汉诺塔I
题目链接:https://www.nowcoder.com/questionTerminal/7d6cab7d435048c4b05251bf44e9f185
题目大意:
略
分析:
利用汉诺塔与二进制的关系来做。
如何用二进制解汉诺塔:https://www.bilibili.com/video/av7398130/
代码如下:

1 class Hanoi { 2 public: 3 // 计算x的二进制位数 4 inline int getBits(int x) { 5 int cnt = 1; 6 while(x >>= 1) ++cnt; 7 return cnt; 8 } 9 10 vector<string> getSolution(int n) { 11 vector< string > ans; 12 string s[3] = {"left", "mid", "right"}; 13 vector< int > arr; 14 arr.resize(n, 0); 15 // tot表示总移动次数 16 int tot = (1 << n) - 1; 17 int cnt = 0; 18 while(cnt++ < tot) { 19 int lowbit = cnt & (-cnt); 20 int bitlen = getBits(lowbit) - 1; 21 int b = 1 + (n - bitlen) % 2;// 偏移,b = 1往右,b = 2往左 22 ans.push_back("move from " + s[arr[bitlen]] + " to " + s[(arr[bitlen] + b) % 3]); 23 arr[bitlen] = (arr[bitlen] + b) % 3; 24 } 25 return ans; 26 } 27 };
汉诺塔II
题目链接:https://www.nowcoder.com/questionTerminal/b2d552cd60b7415fad2612a32e799812?toCommentId=2927834
题目大意:
略
分析:
先给出4个盘子的表(三根柱子的序号分别为0, 1, 2):
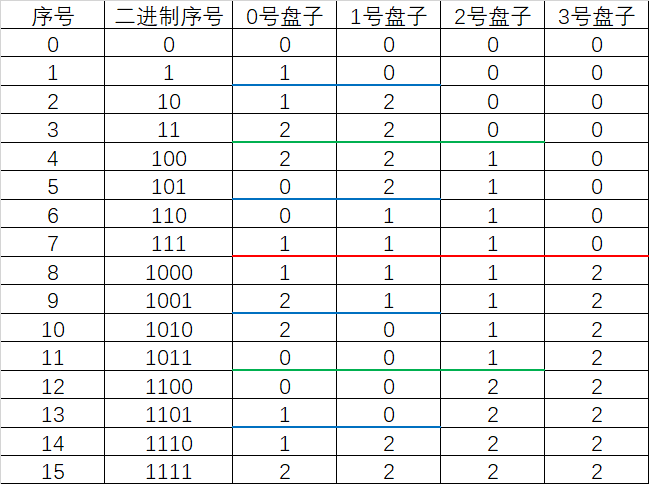
容易看出n个盘子需要移动2n次。
首先我们看红线分割的两块,令8~15行的0号,1号,2号盘子的位置加上2再模3,他们的数值刚好等于0~7行的0号,1号,2号盘子的位置。
再看绿线分割的0~7行,另4~7行的0号,1号盘子的位置加上1再模3,他们的数值刚好等于0~3行的0号,1号盘子的位置。
发现规律了没有?
比如有汉诺塔的位置序列[2, 1, 1, 2],序列最后一个数为2,于是step([2, 1, 1, 2])就等于1000B + step([(2 + 2) % 3, (1 + 2) % 3, (1 + 2) % 3]) = 1000B + step([1, 0, 0]),然后step([1, 0, 0])的最后一个数为0,于是step([1, 0, 0]) = step([1, 0]),直接往前进,并不需要上移,同理step([1, 0]) = step([1]), 对于step([1]),只有一个数字,直接取值,所以step([2, 1, 1, 2])最终等于1001B。
再比如有汉诺塔的位置序列[2, 0, 1, 2],序列最后一个数为2,于是step([2, 0, 1, 2])就等于1000B + step([(2 + 2) % 3, (0 + 2) % 3, (1 + 2) % 3]) = 1000B + step([1, 2, 0]),然后step([1, 2, 0])的最后一个数为0,于是step([1, 2, 0]) = step([1, 2]),step([1, 2])的最后一个数字是2,于是step([1, 2]) = 10B + step([(1 + 2) % 3]) = 10B + step([0]), 对于step([0]),只有一个数字,直接取值,所以step([2, 1, 1, 2])最终等于1010B。
简单来说,就是末尾数字为0,就不变;末尾数字不为0,就让前面的数字加上这个数字再模3,然后求子问题,同时要加上这一位的权值,比如它是第5个数字,就要加上10000B;如果是第3个数字,就要加上100B。
不要问我原理,我是结合二进制找规律找出来的。
代码如下:

1 class Hanoi { 2 public: 3 int chkStep(vector<int> &arr, int n, int b = 0) { 4 if(n == 0) return 0; 5 int tmp = (arr[n - 1] + b - 1) % 3 ; 6 return (1 << (n - 1)) * (tmp != 0) + chkStep(arr, n - 1, b + tmp); 7 } 8 };



