小流域设计洪水计算

       小流域通常是指集水面积不超过数百平方公里的小河小溪，但并无明确限制，一般认为流域面积在300～500km²以下可认为是小流域。从水文角度看小流域具有流域汇流以坡面汇流为主、水文资料缺乏、集水面积小等特性。小流域设计洪水计算，与大中流域相比，有许多特点，并且广泛应用于铁路、公路的小桥涵、中小型水利工程、农田、城市及厂矿排水等工程的规划设计中，因此水文学上常常作为一个专门的问题进行研究。小流域设计洪水计算的主要特点是：

（1）绝大多数小流域都没有水文站，即缺乏实测径流资料，甚至降雨资料也没有。因此小流域设计洪水计算一般为无资料情况下的计算。

（2）小流域面积小，自然地理条件趋于单一，拟定计算方法时，允许作适当的简化，即允许作出一些概化的假定。例如假定短历时的设计暴雨时空分布均匀。

（3）小流域分布广、数量多。因此，所拟定的计算方法，在保持一定精度的前提下，将力求简便，一般借助水文手册即可完成。

（4）小型工程一般对洪水的调节能力较小，工程规模主要受洪峰流量控制，因此对设计洪峰流量的要求高于对洪水过程线的要求。

 

       小流域设计洪水的计算方法较多，归纳起来主要有：推理公式法、地区经验公式法、历史洪水调查分析法和综合瞬时单位线法。其中应用最广泛的是推理公式法和综合瞬时单位线法。它们的思路都是以暴雨形成洪水过程的理论为基础，并按设计暴雨→设计净雨→设计洪水的顺序进行计算。

 

1．小流域设计暴雨的计算

        针对小流域水文资料缺乏的特点，设计暴雨推求常采用以下步骤：

        ①根据省（区）水文手册（包括有关的水文图集，如《暴雨径流查算图表》）中绘制的暴雨参数等值线图，查算出统计历时的流域设计雨量，如24h设计暴雨量等；

        ②将统计历时的设计雨量通过暴雨公式转化为任一历时的设计雨量；

        ③按分区概化雨型或移用的暴雨典型同频率控制放大，得设计暴雨过程。

（1）统计历时的设计暴雨计算

       由各省区的《暴雨径流查算图表》和《水文手册》查取。例如湖北省1985年印发的《暴雨径流查算图表》中，就提供了7d、3d、24h、6h、1h及10min的暴雨参数等值线图，C_s/C_v值全省统一用3.5。据此，便可由设计流域中心点位置查出那里的某统计历时暴雨的均值、C_v 及C_s/C_v，进而求得该统计历时设计频率的雨量。

（2）用暴雨公式计算任一历时的设计雨量

      大量资料的统计成果表明，暴雨强度和历时的关系可用指数方程来表达，它反映一定频率情况下所取历时的平均降雨强度与t的关系，称为短历时暴雨公式。暴雨公式最常见的形式为：

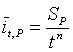  （5.4-1）

 

 

式中：为历时为t，频率为P的最大平均暴雨强度（mm/h）；S_P为t =1.0h的最大平均暴雨强度，与设计频率P有关，或称雨力（mm/h）；t为暴雨历时（h）；n为暴雨衰减指数。

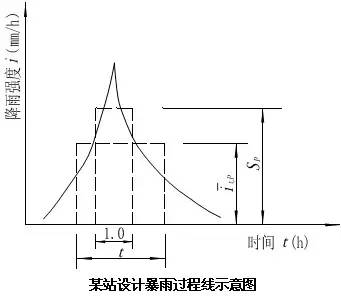
暴雨衰减指数n与历时长短有关，随地区而变化。根据自记雨量资料分析，大多数地区n在t=1h的前后发生变化，t＜1h为n₀，1～24h为n₂。n₀、n₂各地不同，各省区已根据每个站所分析的n₀、n₂绘成了等值线图或分区查算图。

雨力S_P与设计频率P有关，可由该站的设计24h雨量H_24,P推求。因为任一历时t的设计雨量H_t,P为：

 

当t＝24h时，H_t,P＝H_24,P ，n＝n₂，代入上式，得：

 

 

有了S_P和n（n₀或n₂），就可按式（5.4-2）和式（5.4-3）求得设计所需的任一历时的最大平均降雨强度和H_t,P。

有很多省区将该省许多自记雨量记录，根据各历时t对应降雨量H_t，以lgH_t（取对数）为纵坐标，lgt（取对数）为横坐标点图，发现除在1.0h的地方有明显转折外，在6h附近也有明显转折，因此，采取逐段控制的方法求任一历时的设计雨量，如下图所示。即对设计地点，根据《暴雨径流查算图表》）中绘制的暴雨参数等值线图，查算出统计历时的流域设计雨量，求统计历时为10min、1h、6h、24h的设计雨量H_10min、, H₁、H₆、H₂₄，将对应点绘在双对数纸上（如下图所示），连成一条连续折线，从而可查取任一历时t的设计雨量H_t,P 。在已知H_24,P及折线各段n的情况下，可根据直线内插法原理，采用计算法推求任一历时t的设计雨量H_t,P ，读者可参考其他资料自行推导计算公式。

 

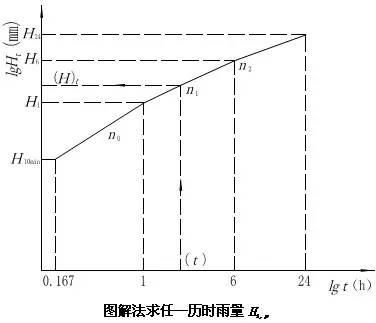
（3）设计面雨量计算

根据上述方法可求得设计流域中心点的各种历时的点暴雨量，应用时需要将点暴雨量转换成流域平均暴雨量，即面雨量。在各省区的水文手册中，刊有不同历时暴雨的点面关系图或点面关系表，可供查用。

（4）设计暴雨的时程分配

在用综合单位线推求小流域设计洪水中，需要计算设计暴雨过程。这时常采用分区概化时程分配雨型来推求。分区概化时程分配雨型就是对一个水文分区的实测暴雨过程，按暴雨特性，如设计历时中的雨峰个数、主雨峰位置、各时段雨量占总雨量的比例进行统计分析，所综合概括出的反映该区暴雨时程分配主要特征和满足工程设计基本要求的一种设想的用相对值表示的降雨分配过程。如下表就是某省第二水文分区的概化时程分配雨型。目前各省区的水文手册或水文图集中均载有此类概化雨型，供缺乏资料情况下推求设计暴雨过程时使用。

 

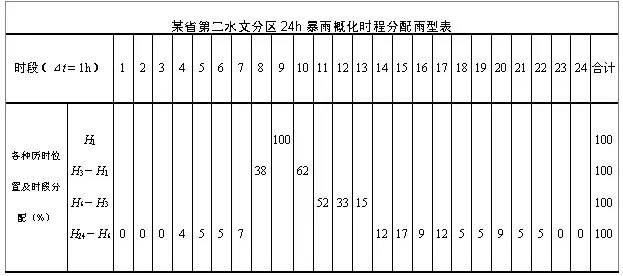
【实例5-9】 小流域设暴雨过程推求

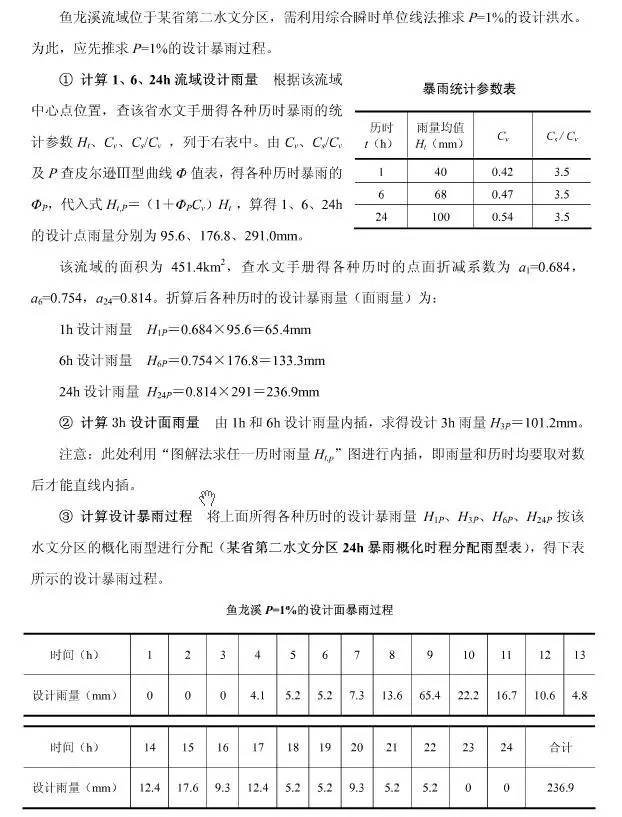
2．用推理公式法推求设计洪峰流量

 

推理公式法是由暴雨资料推求小流域设计洪水的一种简化方法。该法已有一百多年的历史，至今仍在国内外广泛应用。推理公式的形式多种多样，我们介绍在水利水电部门应用的公式。

（1）推理公式法的基本原理

由于流域上各点所形成的净雨距离出口断面的远近不同，加上坡面与河槽的调蓄作用，各净雨点汇集到流域出口断面的速度和时间都不一样。

把净雨从流域最远点A到出口断面B所经历的时间，称为流域最大汇流历时，简称流域汇流历时，以τ表示。

把净雨从流域最远点A到出口断面B所经历的流程长度称最大流程长度，以L表示。净雨在单位时间所通过的距离，叫做汇流速度，以v_τ表示。

在流域上把净雨汇流历时相等的点，连成一组等值线，叫做等流时线，如下图所示。图中单元汇流历时为Δτ。每条等流时线上的水质点，将在同一时间内到达出口断面。流域汇流历时τ＝mΔτ。于是第一条等流时线上的净雨，经一个Δτ时间到达出口断面；第二条等流时线上的净雨，则经2Δτ时间到达出口断面，依此类推。两条等流时线间所包围的面积称为共时径流面积，用f₁、f₂、f₃……表示。显然共时径流面积的总和为流域面积F。

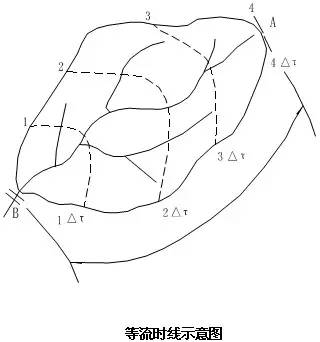
根据等流时线的汇流原理可知，在任意时刻t，出口断面的流量Q_t，显然是由第一块面积f₁上本时段净雨h_t，加上第二块面积f₂上前一时段的净雨h_t－1，再加上第三块面积f₃上前二时段净雨h_t－2……等项乘积之和组成。其各项通式为：

 （5.4-4）

 

由于是小流域面积小，流域汇流历时短，可假定净雨时空分布均匀，即时段Δt内h_t /Δt、h_t－1/Δt、h_t－2/Δt……相等，且等于流域平均净雨强度i，则上式可简化为：

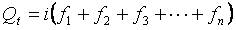（5.4-5）

 

当净雨历时t_c≥τ时，出口断面的洪峰流量Q_m由τ历时内最大净雨量h_τ在全流域面积F上所形成，称全面汇流造峰，洪峰流量为Q_m＝i·F，其中i＝h_τ／τ，即：

（5.4-6）

 

  式中：Q_m为流域出口断面的洪峰流量（m³/s）；

          τ为流域汇流历时（h）；

         h_τ为τ历时内的最大地面净雨深（mm）；

         0.278为单位换算系数；F为流域面积（km²）。

        式（5.4-6）中，历时为τ的地面净雨深h_τ，根据下图由下式计算：

 

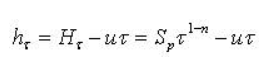（5.4-7）

 

式中H_τ为历时为τ的暴雨量（mm），u为产流参数（mm/h）。

 

当净雨历时t_c＜τ时，出口断面的洪峰流量Q_m由相当于产流历时t_c内的最大净雨量h_R在部分流域面积F₀（是指汇流历时相差t_c的两条等流时线在流域中包围的最大面积，又称最大等流时面积）上所形成，称部分汇流造峰，洪峰流量为Q_m＝i·F₀，其中i＝h_R／t_c，即：

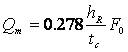（5.4-8）

 

  式中Q_m为流域出口断面的洪峰流量（m³/s）；

         t_c为净雨历时（h）；

         h_R为t_c历时内的最大地面净雨深（mm）；

         0.278为单位换算系数，F₀为部分面积（km²）。

 F₀与流域形状、汇流速度v_τ、净雨历时t_c等因素有关，详细计算比较复杂，生产实际中一般采用简化法，假定F₀随汇流时间的变化可概化为线性关系，即：

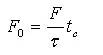（5.4-9）

 

将上式代入式（5?42），可得部分汇流情况下计算洪峰流量的简化公式为：

 

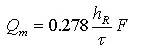(5.4-10)

 

式（5.4?10）中，历时为t_c的地面净雨深h_R，根据下图，可由下式计算：

（5.4-11）

 

式中Ht_c为历时为t_c的暴雨量（mm），u为产流参数。

 

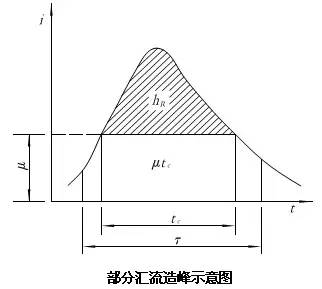
通过推导，净雨历时t_c可用下式计算：

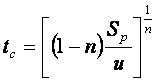（5.4-12）

 

引入水力学中计算流域平均汇流速度的半经验公式，即：

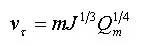（5.4-13）

 

  式中，v_τ为沿L的平均汇流速度（m/s）；

                      J为沿L的平均坡降，以小数计；

                       Q_m为流域出口断面的洪峰流量（m³/s）；

                   m为汇流参数，m与流域和河道情况等条件有关。

  那么流域汇流时间τ的计算公式为：

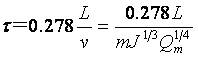（5.4-14）

 

     式中τ、L的单位分别为h及km，其它符号意义及单位同前。

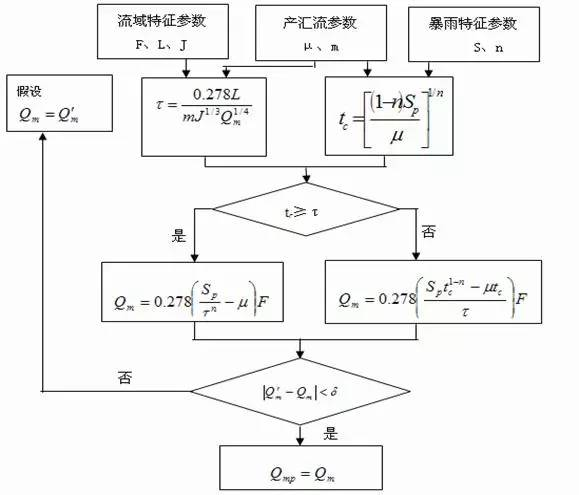
综合式（5.4?6）、式（5.4?7）、式（5.4?10）、式（5.4?11）和式（5.4?14），推理公式法计算设计洪峰流量就是要联解如下一组方程：

 

 

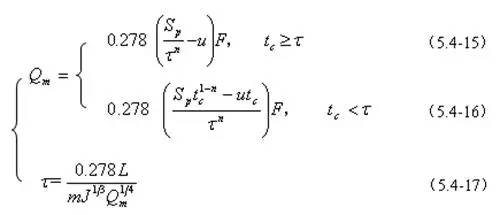
（2）参数的推求

 

由上述的方程组可知，要求解Q_m与τ，必须首先确定方程组中的各个参数，即流域特征参数F、L、J；暴雨参数S_p、n；产流参数u，汇流参数m。

流域特征参数的推求可参阅1.2的有关内容；暴雨参数的推求可参阅本节的有关内容，因此关键是推求产流参数u和汇流参数m。

产流参数u代表产流历时t_c内陆面平均入渗率，又称损失参数，以mm/h计。推理公式中假定流域各点的损失相同，把产流历时内的损失视为常数。u值的大小与所在地区的地表透水性能、地貌、植被、暴雨量的大小及分配、前期影响雨量等因素有关。

汇流参数m是汇流速度公式中一个经验性系数，用以说明洪水汇集的特性。m值与河槽及山坡的糙率、流域地形、地貌、植被、河网的调蓄作用、河道断面形状及暴雨的时空分布等因素有关。

各省区为了推求u、m值，分析了大量的暴雨洪水资料，提出了各自的方法。一般是根据实测暴雨洪水资料反算u、m值，然后进行地区综合，建立图（表）或经验公式，供无资料地区查算u、m值。在生产实践中，可以查各省区的水文手册（图集）。

例如福建省在进行综合时，由于全省各地的u值相差不大，因此建议设计条件下，全省采用u＝3.5mm/h；江西省在进行综合时，把全省分为4个区，设计条件下每区取一个相同的u值，全省的u值范围为1.0～2.0mm/h。

例如四川省综合单站分析m值，建立了m～f （θ）的经验关系，其中θ＝L/（J^1/3F^1/4）。当θ＝1～30时，m＝0.40θ^0.204；当θ＝30～300时，m＝0.092θ^0.636。

（3）设计洪峰流量的计算方法

应用推理公式计算设计洪峰流量的方法很多，常用的方法有：试算法和图解法。

1）试算法　该法是以试算方式联解式（5.4-15）、式（5.4-16）、式（5.4-17），步骤如下：

① 通过对设计流域调查了解，结合水文手册及流域地形图，确定流域的几何特征值F、L、J，设计暴雨的统计参数（均值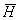及C_v、C_s / C_v）及暴雨公式中的参数n（或n₀、n₁、n₂），损失参数u及汇流参数m。

② 计算设计暴雨的S_p，并利用式（5.4-12）计算设计净雨历时t_c。

③ 将F、L、J、S_p、t_c、u、m代入式（5.4-15）、式（5.4-16）、式（5.4-17），其中仅剩下Q_m、τ未知，两个方程解两个未知量，故可求解。

④ 用试算法求解。先设一个Q_m，代入式（5?51）得到一个相应的τ，将它与t_c比较，判断属于何种汇流情况，再将该τ值代入式（5.4-17）或（5.4-16），又求得一个Q’_m，若Q’_m与假设Q_m的一致（误差不超过1%），则该Q_m及τ即为所求；否则，另设Q_m重复上述步骤试算，直到满足要求为止。

 

【实例5-10】 推理公式法推求洪峰流量

2）图解法

 

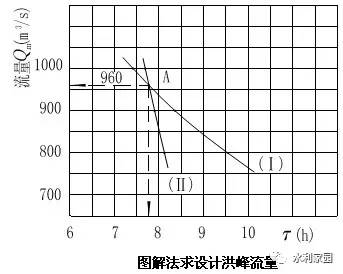
首先假定为全面汇流造峰，于是利用式（5.4-15）和式（5.4-17）联解推求洪峰流量。即假定一组洪峰流量Q_mi，代入式（5.4-15）求得一组相应的τ_i；再代入式（5.4-17）求得另一组相应的τ'_i；。将（Q_mi，τ_i）和（Q_{mi<, ub="">}，τ’_i）绘成关系曲线，如下图所示。两曲线的交点A的纵、横坐标即为所求的设计洪峰流量Q_mp及流域汇流历时τ。

 

计算完成后，由式（5.4-12）计算t_c，并与所求的值进行比较，若t_c≥τ，原假定为全面汇流条件成立；若t_c＜τ，则改由式（5.4-16）和式（5.4-17）联解推求洪峰流量，重复上述计算，并重新绘制下图推求设计洪峰流量Q_mp及流域汇流历时τ。

实例【5-11】

根据实例【5-10】所给的基本资料，用图解法求百年一遇设计洪峰流量

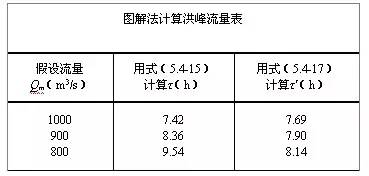
① 首先假定为全面汇流造峰，于是利用式式（5.4-15）和式（5.4-17）联解推求洪峰流量。全部计算列如下表中。

② 将下表中的数值点如上图，则两曲线的交点A的纵、横坐标为所求的设计洪峰流量Q_mp及流域汇流历时τ，即Q_mp=960m³/s，τ=7.77h。

③ 验算：由实例【5-10】可知t_c=16.2h，可见t_c＞τ，原假定为全面汇流条件成立。

       上述两种方法，侧重于阐明水科院推理公式法求解设计洪峰流量的基本原理和方法。各省区的具体做法不尽相同，有的省区还作了许多简化处理，应用推理公式法时，要注意参考本省区暴雨洪水图集或手册。

推理公式法假定降雨的时空分布及产流强度均匀，这在设计条件下的小流域是允许的，但实际的降雨产流不可能出现这种情况，因此推理公式法不适用于推求实际暴雨形成的洪水，而比较适用于推求设计暴雨所形成的设计洪峰流量。

3．由地区经验公式计算设计洪峰流量

       根据一个地区内的小流域实测和调查的暴雨洪水资料，直接建立主要影响因素与洪峰流量间的经验相关方程，即洪峰流量地区经验公式。把它应用于该地区无资料流域推求设计洪峰流量时，就是地区经验公式法。经验公式不着眼于流域的产汇流原理，只进行该地区资料的统计归纳，故地区性很强。一般地说，由哪个地区资料建立的公式，只适用于哪个地区，借用其他地区的经验公式，要格外小心，必须用本地区一定的资料进行检验。

地区经验公式比较简单，应用方便，如果公式能够考虑到影响洪峰的因素，且公式的研制采用了可靠的并具有一定代表性的资料，则计算成果可以有相当好的精度。许多省区的水文手册中都载有各自的公式及使用方法。

（1）以流域面积为参数的地区经验公式

       最简单的经验公式认为流域面积是影响洪峰流量的主要因素，而把其他因素用一些综合性的参数表达，公式的形式为

（5.4-18）

  式中：Q_mp为频率为p的设计洪峰流量（m³/s）；

                               F 为流域面积（km²）；

                               n、C_p为经验指数和系数。

上述公式使用简单方便。制作这种公式要求的资料条件较高，因为只有分区比较小，才有照顾到分区内除F之外的其他影响因素都比较一致。但分区小，又难以保证区内会有比较多的长系列水文站资料。所以，当资料不足时，应考虑多参数地区经验公式。

（2）包含降雨因素的多参数地区经验公式

多参数经验公式是以流域特征与设计暴雨等主要影响因素为参数建立的。它认为洪峰流量主要受流域面积、流域形状与设计暴雨等因素影响，而其它因素可用一些综合参数表达，公式的常见形式为

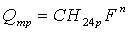（5.4-19） 

（5.4-20）

（5.4-21）

 

式中：H_24p、h_24p分别为频率为p的年最大24h暴雨量及净雨量（mm）；

                      J为河道干流平均坡度；

                      f为流域形状系数（f=F/L²）；

                     C为经验系数；α、β、γ、n为经验指数。

例如，安徽省山丘区中小河流洪峰流量经验公式为：

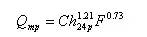（5.4-22）

 

该省把山丘区分为深山区、浅山区、高丘区、低丘区4种类型，其C值分别为0.0541、0.0285、0.0239、0.0194。24h设计暴雨H_24p按等值线图查算，并通过点面关系折算而得。设计净雨：深山区按h_24p =H_24p -30计算，浅山区、丘陵区按h_24p =H_24p -40计算。

4．设计洪水过程线的推求

       一些中小型水库工程，具有一定的调节能力。为了分析水库调洪能力、防洪效果及防洪建筑物的设计，除推求设计洪峰流量外，还要推求设计洪水过程线。用于计算小流域设计洪水过程线的方法有综合单位线法和概化过程线法。综合单位线法包括综合时段单位线（指经验单位线）和综合瞬时单位线。近年来，随着瞬时单位线的推广应用，我国大部分省区在分析大量暴雨洪水的基础上建立了瞬时单位线参数的地区综合公式，并载于水文手册或图集中。由于综合瞬时单位线具有一定的数学模型，综合和使用方便，我国大部分省区已经用综合瞬时单位线取代综合时段单位线来推求小流域的设计洪水过程。

        配合推理公式法或地区经验公式法所计算的设计洪峰流量，通常是拟定一条相应的概化设计洪水过程线，即可满足要求。所谓概化洪水过程线是指由地区上各流域的实测洪水过程线综合分析而得出的具有一定代表性的洪水过程线。概化的线

型有三角形、五点形、多峰形和标准概化过程线等。这里只介绍综合瞬时单位线法和三角形概化过程线法，其它方法请参考有关资料或各省区的水文手册。

（1）综合瞬时单位线法

      1）综合瞬时单位线法的基本概念

      纳希瞬时单位线完全由参数n、K决定。因此，瞬时单位线的综合，实质上就是参数n、K的综合。不过，在实际工作中并不直接去综合n、K，而是综合n、K有关的参数m₁和m₂，或综合m₁和n。由纳希瞬时单位线方程可导出m₁和m₂与n、K的关系为：

（5.4-23）

（5.4-24）

 

许多地区的经验表明，一个流域的n值比较稳定，可取为常数。瞬时单位线的一阶原点矩（习惯上称为单位线的滞时）m₁则与平均净雨强度i有比较好的非线性关系，即：

（5.4-25）

 

 式中：i为平均地面净雨强度（mm/h）；

          a、λ为反映流域特征的系数和非线性指数，对于固定流域均可取为常数，通过i与m₁的关系求得。

        对瞬时单位线的综合，一般分两步进行：首先，考虑净雨强度影响，在对m₁和m₂做地区综合之前，根据瞬时单位线非线性变化规律，求得统一标准净雨强度的m₁和m₂（或n）值，称标准化参数。这个标准一般定为净雨强度i=10mm/h，相应的m₁记为m_1,10，称标准化的m₁。同时还要对非线性影响指数λ做地区综

合。其次，是对各流域统一标准的m₁和m₂进行地区综合，建立这些标准化的m₁、m₂与流域特征间的关系。当这些关系建立起来之后，便可用以推求无资料流域的单位线了。

      2）m1、m2的标准化与λ的地区综合

    根据式（5-59），考虑净雨强度对瞬时单位线的影响，取i=10mm/h时，m₁= m_1,10，得m_1,10=a×10^-λ，则a=m_1,10×10^λ，将其代入式（5-59）得

 

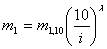（5.4-26）

 

上式一方面可用来使m₁标准化，即由m₁、i求m_1,10；另一方面，当已知m_1,10时，可由i计算相应的m₁，以便进一步推求净雨i形成的洪水过程。

实际资料表明，指数λ与流域面积F（km²），干流河道坡度J（千分率）、干流河道长度L（km）等流域特征有比较密切的关系，如四川省第一水文区的关系为

 

 

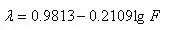（5.4-27）

 

必须注意，净雨强度增加到一定程度后，由于河水漫滩等水力条件的限制，m₁不会无限度地减小，因此，各省区都规定了使用式（5.4-26）的临界雨强i_临，即设计雨强超过i_临以后，不再进一步做非线性改正，使滞时维持在

 

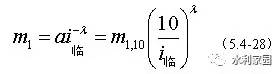
的水平。例如四川省规定的i_临=50mm/h。

     雨强对m₂（或n）的影响甚微，一般都不需要做非线性改正，而把m₂（或n）直接作为标准化的情况。

3）m1,10及n（或m2）的地区综合

   瞬时单位线的标准化参数m_1,10和n与流域特征之间存在着一定的关系，可以通过回归分析建立经验公式以定量地表达这种关系。例如四川省第一水文分区的公式为

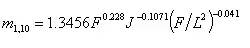（5.4-29）

 

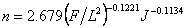（5.4-30）

 

以上诸式中m_1,10、F、L、J的单位分别为h、km²、km、千分率。这类公式都刊于各省区的暴雨径流查算图表等手册中，可供查用。

 

     4）综合瞬时单位线推求设计洪水过程

 

   对于无实测资料的中、小流域，用综合瞬时单位线法推求设计洪水过程的步骤如下：

 

   ① 根据产流计算方法，由流域的设计暴雨推求设计净雨过程。

 

   ② 将流域几何特征代入瞬时单位线参数地区综合公式求m_1,10及n（或m₂）。

 

   ③ 按设计净雨由m_1,10求出设计条件的m₁，并由上一步的n 求K， K= m₁/n。

 

   ④ 选择时段单位线的净雨时段Δt，按5.3.4 介绍的方法由n、K求时段单位线。Δt一般取为单位线涨洪历时t_r的1/2～1/3，即Δt＝（1/2～1/3）t_r，。初定Δt时可参考广东省建议的数据，如下表。

时段单位线适宜净雨时段与流域面积的关系
流域面积F（km2）	＜5	5～15	15～100	100～350	350～1000
适宜净雨时段Δt（h）	1/3	1/2	1	2	3

⑤ 由设计净雨过程及时段单位线求得设计地面径流过程。

⑥ 按各省区水文手册或有关设计单位建议的计算方法确定设计条件下的地下径流流量。

⑦地面、地下径流过程按相应时刻叠加，即得设计洪水过程。

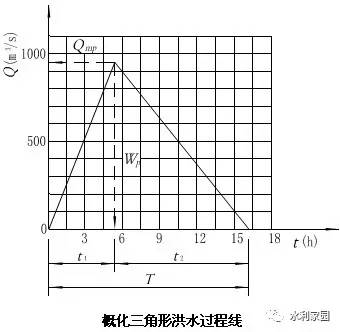
（2）三角形概化过程线法

三角形概化过程线是一种最简单的概化洪水过程线。当洪水陡涨陡落时，可假定流量为直线变化，如下图所示。三角形洪水过程线的设计洪峰流量Q_mp，可由前述推理公式法或地区经验公式法求得，设计洪量可用下式计算：

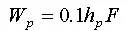（5.4-31）

 

  式中：                          W_p为设计洪水总量（10⁴m³）；

                                       F为流域面积（km²）；

                                       h_p为设计净雨总量（mm），可由最大24h设计暴雨量扣除损失后求得；

                                      0.1为单位换算系数。

 

设计洪水总历时为

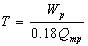（5.4-32）

 

式中：T为设计洪水总历时（h）； 

           Q_mp为设计洪峰流量（m³/s）；

           W_p为设计洪水总量（10⁴m³）；

          0.18为单位换算系数。

由上图可知，T=t₁+t₂。t₁为涨洪历时，t₂为退洪历时。一般情况下，t₂＞t₁，根据有些地区分析，t₂/t₁在1.5～3.0之间。当Q_mp、T、t₁确定之后，便可作出三角形过程线。如果小流域地下水补给丰富，还应加上基流，得到设计洪水过程线。

三角形洪水过程线虽然与实际洪水过程线的情况相差较大，但小型水利工程在调洪过程中起控制作用的是洪峰段，而起涨段与退水段的形状对调洪影响不大，所以仍有其实用价值。