博弈论 斯坦福game theory stanford week 5.0_
博弈论 斯坦福game theory stanford week 5-0
repeated Games 重复游戏
在实际的博弈中,很多的情况不止一次的发生,下面有很多的例子:
- 市场中的公司中的博弈
- 政治的博弈
- 朋友间的交换
- 工人们的相互竞争合作
我们讨论一个案例,那就是opec
他们的油价其实是一个很有趣的博弈:
- 1930年的油价是20,他们相互的竞争
- 1950年,他们开始合作,减少石油的产量,然后油价就开始上升
- 1982 变成来 90元
- 2002年,他们的合作渐渐的减少,油价也开始了下降
他们在这个过程中使用了合作行为。cartel,卡特尔是一种像囚徒困境的一种困局
- 这样的合作需要密切的观察自己的朋友,并且快速的惩罚不合作的博弈者
- 并且需要大多数的博弈者有长远的打算
- 战争并不能达到更大的利益
要衡量这些合作的最终的结果,我们使用一次一侧的进行博弈的方式。
infinitely repeated games: utility 无限重复的游戏,效益
我们要定义游戏的效益。
我们是不是能够把这种情况用拓展形式表现出来呢?
我们这样的博弈是一个无止境的博弈,我们是不是可以这样表示呢?
不过这种无限的形式写出来,我们基本上是无法计算博弈的结果的,因此我们上面学习的表达方式并没有帮助。

因为无限的序列让我们没有办法计算收益,我们可以将我们的收益写成极限形式,就像上面的公式。
那么我们的收入就会变成了平均收入或者稳定收入。
第二个定义是有关未来的利益的未来的尚未计算的收益,

这个收益描述了一种长期的收益,是有关未来的收益预期,他的计算方法是通过一个因此乘上未来的收益,然后求和。
比如我进行投资的时候,可能会先投入大量的前期投入,然后再逐渐的盈利,但是这样做的人有很多,他们主要考虑的就是未来的收入可以非常完美的覆盖现在的付出。
但是未来的收入会有一个贬值因子,因为这里的收入不是立刻马上兑现的,因此我们不能把他们当成100%的金钱看待。
stochastic games 随机博弈
如果我们不借用之前同步博弈的想法,我们说随机博弈是一种重复比赛的概念
在这种博弈中:
- 博弈者随机的从所有的行为集合中选择
- 博弈的进行取决于所有热的之前的选择和之后的选择。
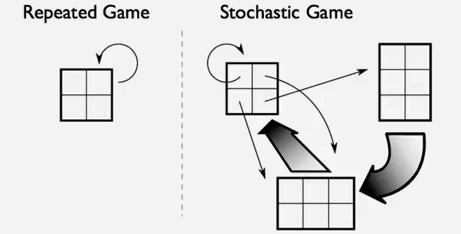
下面有一个示图来讨论这个问题。
再重复博弈中,我们的图形只能被博弈者的行为影响,一次又一次的旋转。但是再随机的博弈中,博弈者可以去选择其他的游戏,而不只是拘泥于单一的游戏中。

这是博弈的完整的定义。
我们,定义了
- 状态集Q
- 博弈者集N
- 行为集合A
- 转移概率函数P(q,a,q'),描述一个行为a下从一个状态q转移到另一个状态q'的概率。
- 真实收益函数R,描述博弈者的真实收益。
为了简化问题,我们常常假设策略空间再所有的游戏中都向图
可以形成马尔科夫简单代理随机博弈。
重复游戏中的学习
我们会学习到学习的两种形式,在重复游戏中的两种形式。
- fictitious play 虚构游戏
- No-regret learning 无悔学习
不过大体上,在博弈论中的学习是一个比较火热的领域,我们有很多的知识没有接触。
虚构游戏
从纳什均衡开始学习
每一个博弈者explicit对其他的博弈者的行为有一个明确的信念。
他们开始的信念是一种敌对的信念。
在每一回合后,每个博弈者都会评估其他人的策略。
观察对手的行为和结果。
下面我们进行刚刚说的策略的形式化的表述。
- 对于每一个行为a,让w(a)作为其他人使用行为a的次数
- 评估的方法就是他们的收益。
使用如下的公式:
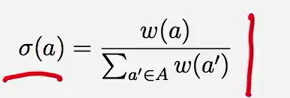
我们举个例子来说,比如说猜硬币游戏,他的博弈的图表是这样的:
| T | H | |
|---|---|---|
| T | 3 ,-3 | -2,2 |
| H | -2,2 | 1,-1 |
那么我们可以假设情况是这样的
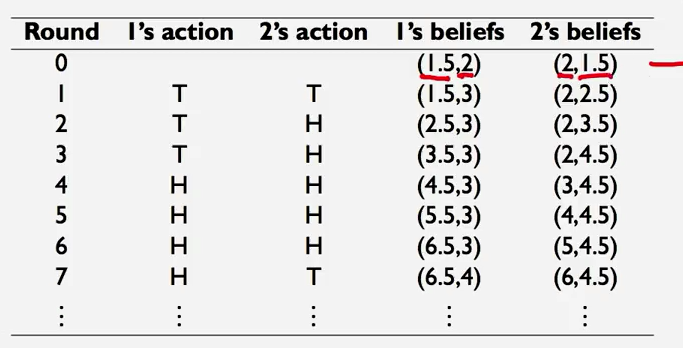
在这样的情况下,均衡的情况是会出现的,而且在这种请款下,最终会达到纳什均衡。
无悔学习
首先我们要定义什么是后悔

后悔的定义是这样的,


