斯坦福-随机图模型-week3.2_

斯坦福-随机图模型-week3.2

独立马尔科夫网络

分离的概念

分离的概念是这样的，如果我们有这样的定义：

如果再H中没有没有实际的连接线，我们认定Z呗H分离

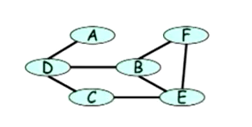
比如再这个图中，图A和E是被B和C分离的。

factorizes over

如果P再H下被分解，那我可以认为

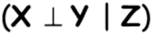
I-maps 和 完美图

我我们接下来讨论如何来使用一个适合图的结构的的分布。

因子∅：从Val(D)映射到实数域R的一个函数。除非另行说明，只关注非负的因子。

随机变量集合D。

变量集D称为因子的辖域。

∅越大，两个值的兼容性越好。

因子的运算：

马尔科夫网中将联合概率分布和CPD都用因子表示了：令表示那么

完备子图和极大团

团：团是一个两两之间有边的顶点集合。

最大（极大）团：一个团不被其他任何一个团包含则为最大团。

完备子图：最大团集合的子集。

主线概念——吉布斯分布和马尔科夫网

吉布斯分布总结起来就是：分布满足因子运算后归一化。

马尔科夫网是随机变量集的无向图模型，侧重表现变量之间的交互影响。马尔科夫网结构用表示。

马尔科夫网和吉布斯分布的关系：

参数化马尔科夫网的因子通常称为团位势。

马尔科夫网简化

这个定义的含义其实很简单：当U确定为u时，马尔科夫网的辖域简化为Y-U（也就是变量集U在马尔科夫网中可以去除掉），所有U不等于u的因子也可以不考虑了。

二． 独立性

基本独立性

马尔科夫网的基本独立性是可靠和完备的，可靠表现在从正向推导I-map完全成立，从反向推导，当P为正分布（所有变量的概率非0）时成立。

严格的完备性不成立，弱化的完备性成立：

独立性关系

马尔科夫三个性：全局独立性（）、成对对立性（）、局部独立性（）。

其中全局独立性上面已经提过了，而成对独立性和局部独立性如下：

三者的关系：

从分布到图

这其实就是根据局部独立性和成对独立性构造最小I-map。具体如下：