基本数据结构
1.线性数据结构
- 线性结构作为最常用的数据结构,其特点是数据元素之间存在一对一的线性关系。
- 线性结构拥有两种不同的存储结构,即顺序存储结构和链式存储结构。顺序存储的线性表称为顺序表,顺序表中的存储元素是连续的,链式存储的线性表称为链表,链表中的存储元素不一定是连续的,元素节点中存放数据元素以及相邻元素的地址信息。
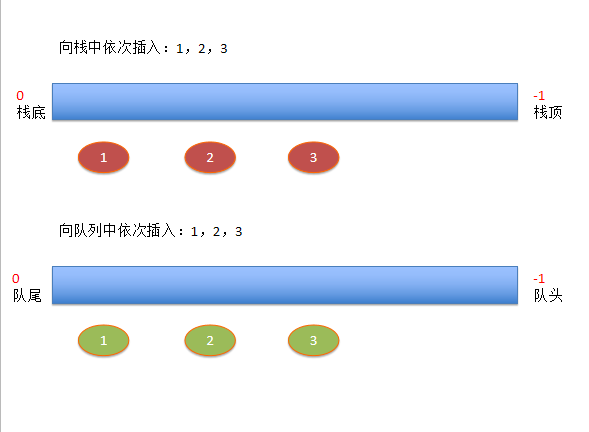
- 线性结构中存在两种操作受限的使用场景,即队列和栈。栈的操作只能在线性表的一端进行,就是我们常说的先进后出(FILO),队列的插入操作在线性表的一端进行而其他操作在线性表的另一端进行,先进先出(FIFO),由于线性结构存在两种存储结构,因 此队列和栈各存在两个实现方式。
2.栈
- 概念:栈(有时称为“后进先出栈”)是一个元素的有序集合,其中添加移除新元素总发生在同一端。这一端通常称为“顶部”。与顶部对应的端称为“底部”。栈的底部很重要,因为在栈中靠近底部的元素是存储时间最长的。最近添加的元素是最先会被移除的。这种排序原则有时被称为 LIFO,后进先出。它基于在集合内的时间长度做排序。较新的项靠近顶部,较旧的项靠近底
- 应用:每个 web 浏览器都有一个返回按钮。当你浏览网页时,这些网页被放置在一个栈中(实际是网页的网址)。你现在查看的网页在顶部,你第一个查看的网页在底部。如果按‘返回’按钮,将按相反的顺序浏览刚才的页面。
1.Python实现栈
- 栈的抽象数据类型定义:栈的抽象数据类型应该由以下结构和操作定义。栈操作如下:
- Stack() 创建一个空的新栈。他不需要参数,并返回一个空栈。
- push(item)将一个新项添加到栈的顶部,他需要item做参数,并不返回任何内容。
- pop() 从栈中删除顶部项,不需要参数并返回item,栈被修改。
- peek() 从栈返回顶部项,但不会删除它,不需要参数,不修改栈。
- isEmpty()测试栈是否为空,不需要参数,并返回布尔值。
- size() 返回栈中的item数量,不需要参数,并返回一个整数。
- 代码实现:Python中的列表类提供了有序集合机制和一组方法。例如,如果我们有列表 [2,5,3,6,7,4],我们只需要确定列表的哪一端将被认为是栈的顶部。一旦确定,可以使用诸如 append 和 pop 的列表方法来实现操作。
alist = [2, 5, 3, 6, 7, 4] class Stack(): def __init__(self): self.items = [] def push(self, item): self.items.append(item) def pop(self): return self.items.pop() def peek(self): return len(self.items) - 1 def isEmpty(self): return self.items == [] def size(self): return len(self.items)
- 应用
stack = Stack() for i in alist: stack.push(i) print('栈顶元素下标:', stack.peek()) print("检测栈是否为空",stack.isEmpty()) print('元素个数:', stack.size()) for i in range(len(alist)): print(stack.pop()) # 执行结果: 栈顶元素下标: 5 False 元素个数: 6 4 7 6 3 5 2
3.队列
- 概念:队列是项的有序结合,其中添加新项的一端称为队尾,移除项的一端称为队首。当一个元素从队尾进入队列时,一直向队首移动,直到它成为下一个需要移除的元素为止。最近添加的元素必须在队尾等待。集合中存活时间最长的元素在队首,这种排序成为 FIFO,先进先出,也被成为先到先得
- 应用:
- 我们的计算机实验室有 30 台计算机与一台打印机联网。当学生想要打印时,他们的打印任务与正在等待的所有其他打印任务“一致”。第一个进入的任务是先完成。如果你是最后一个,你必须等待你前面的所有其他任务打印
用Python实现队列
- 队列的抽象数据类型定义:队列的抽象数据类型应该由以下结构和操作定义。队列操作如下:
-
- Queue() 创建一个空的新队列。 它不需要参数,并返回一个空队列。
- enqueue(item) 将新项添加到队尾。 它需要 item 作为参数,并不返回任何内容。
- dequeue() 从队首移除项。它不需要参数并返回 item。 队列被修改。
- isEmpty() 查看队列是否为空。它不需要参数,并返回布尔值。
- size() 返回队列中的项数。它不需要参数,并返回一个整数。
class Queue(): def __init__(self): self.items = [] def enqueue(self,item): self.items.insert(0,item) def dequeue(self): return self.items.pop() def isEmpty(self): return self.items == [] def size(self): return len(self.items)
- 应用;
queue = Queue() alist = [2, 5, 3, 6, 7, 4] for i in alist: queue.enqueue(i) print("查看队列是否为空", queue.isEmpty()) print("队列中的项数", queue.size()) for i in range(len(alist)): print(queue.dequeue()) # 输出结果: 查看队列是否为空 False 队列中的项数 6 2 5 3 6 7 4
队列的案例: 烫手的山芋
- 烫手山芋游戏介绍:6个孩子围城一个圈,排列顺序孩子们自己指定。第一个孩子手里有一个烫手的山芋,需要在计时器计时1秒后将山芋传递给下一个孩子,依次类推。规则是,在计时器每计时7秒时,手里有山芋的孩子退出游戏。该游戏直到剩下一个孩子时结束,最后剩下的孩子获胜。请使用队列实现该游戏策略,排在第几个位置最终会获胜。
- 准则:手里有山芋的孩子永远排在队列的头部
分析过程:
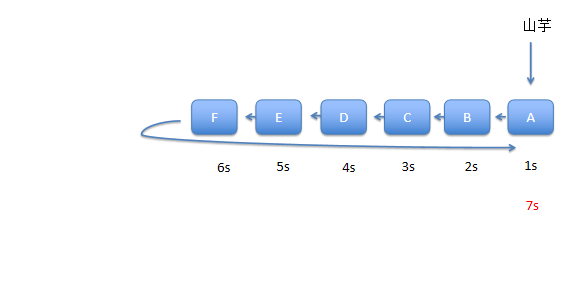

用Python代码实现:
class Queue(): def __init__(self): self.items = [] def enqueue(self, item): self.items.insert(0, item) def dequeue(self): return self.items.pop() def size(self): return len(self.items) queue = Queue() kids = ['A', 'B', 'C', 'D', 'E', 'F'] for kid in kids: queue.enqueue(kid) # A队头,F队尾 while queue.size() > 1: for i in range(len(kids)): # 每循环一次,山芋传递一次,手里有山芋的孩子永远在对头位置 kid = queue.dequeue() queue.enqueue(kid) queue.dequeue() print('获胜的选手是:' + ueue.dequeue()) # 输出结果为; 获胜的选手是: E
- 面试题:如何实现两个队列生成一个栈
class Queue(): def __init__(self): self.items = [] def enqueue(self, item): self.items.insert(0, item) def dequeue(self): return self.items.pop() def size(self): return len(self.items) q1 = Queue() q2 = Queue() alist = [1, 2, 3, 4, 5] # 将数据加入队列 for i in alist: q1.enqueue(i) """ 思路: 1.首先了解:栈先进后出,队列先进先出 2.取值时,将q1前n-1项取出存在q2中,将最后一个值打印出来 """ while True: # 取出前q1的前n - 1项, 放置在q2中 while q1.size() > 1: item = q1.dequeue() q2.enqueue(item) print(q1.dequeue()) # 此时q1位空,q2为原q1的前n-1项,将q1,q2互换,然后进行下次循环 q1, q2 = q2, q1 if q1.size() == 0: break
4.双端队列
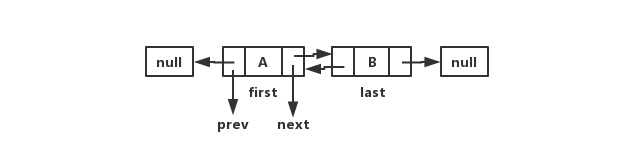
- 概念:deque 即双端队列。(deque,全名double-ended queue)是一种具有队列和栈的性质的数据结构。双端队列中的元素可以从两端弹出,其限定插入和删除操作在表的两端进行。
- 特性:deque 特殊之处在于添加和删除项是非限制性的。可以在前面或后面添加新项。同样,可以从任一端移除现有项。在某种意义上,这种混合线性结构提供了单个数据结构中的栈和队列的所有能力。
- 注意:即使 deque 可以拥有栈和队列的许多特性,它不需要由那些数据结构强制的 LIFO 和 FIFO 排序。这取决于你如何持续添加和删除操作。

- 优缺点:尽管双端队列看起来似乎比栈和队列更灵活,但实际上在应用程序中远不及栈和队列有用。
用Python实现deque
-deque 的抽象数据类型定义:deque的抽象数据类型应该由以下结构和操作定义。其中元素可以从首部或尾部的任一端添加和移除。deque操作如下:
-
- Deque() 创建一个空的新 deque。它不需要参数,并返回空的 deque。
- addFront(item) 将一个新项添加到 deque 的首部。它需要 item 参数 并不返回任何内容。
- addRear(item) 将一个新项添加到 deque 的尾部。它需要 item 参数并不返回任何内容。
- removeFront() 从 deque 中删除首项。它不需要参数并返回 item。deque 被修改。
- removeRear() 从 deque 中删除尾项。它不需要参数并返回 item。deque 被修改。
- isEmpty() 测试 deque 是否为空。它不需要参数,并返回布尔值。
- size() 返回 deque 中的项数。它不需要参数,并返回一个整数。
class Deque(): def __init__(self): self.items = [] def addFront(self,item): self.items.insert(0,item) def addRear(self,item): self.items.append(item) def removeFront(self): return self.items.pop() def removeRear(self): return self.items.pop(0) def isEmpty(self): return self.items == [] def size(self): return len(self.items)
deque 的应用案例- 回文检测
- 回文检测:设计程序,检测一个字符串是否为回文。
- 回文: 回文是一个字符串,读取首尾相同的字符串,例如,radar toot madam。
- 分析:该问题的解决方案将使用 deque 来存储字符串的字符。我们从左到右处理字符串,并将每个字符添加到 deque 的尾部。在这一点上,deque 像一个普通的队列。然而,我们现在可以利用 deque 的双重功能。 deque 的首部保存字符串的第一个字符,deque 的尾部保存最后一个字符。我们可以直接删除并比较首尾字符,只有当它们匹配时才继续。如果可以持续匹配首尾字符,我们最终要么用完字符,要么留出大小为 1 的deque,取决于原始字符串的长度是偶数还是奇数。在任一情况下,字符串都是回文。

class Deque(): def __init__(self): self.items = [] def addFront(self,item): self.items.insert(0,item) def addRear(self,item): self.items.append(item) def removeFront(self): return self.items.pop() def removeRear(self): return self.items.pop(0) def size(self): return len(self.items) def isHuiWen(s): ex = True q = Deque()
# 循环添加元素至双端队列中 for ch in s: q.addFront(ch) while q.size() > 1:
# 判断从后面删除的的元素是否等于从前方删除的元素 if q.removeFront() != q.removeRear(): ex = False break return ex print(isHuiWen('heireh'))
5.顺序表
6.链表
4,待续


 ヾ(≧O≦)〃嗷~
ヾ(≧O≦)〃嗷~