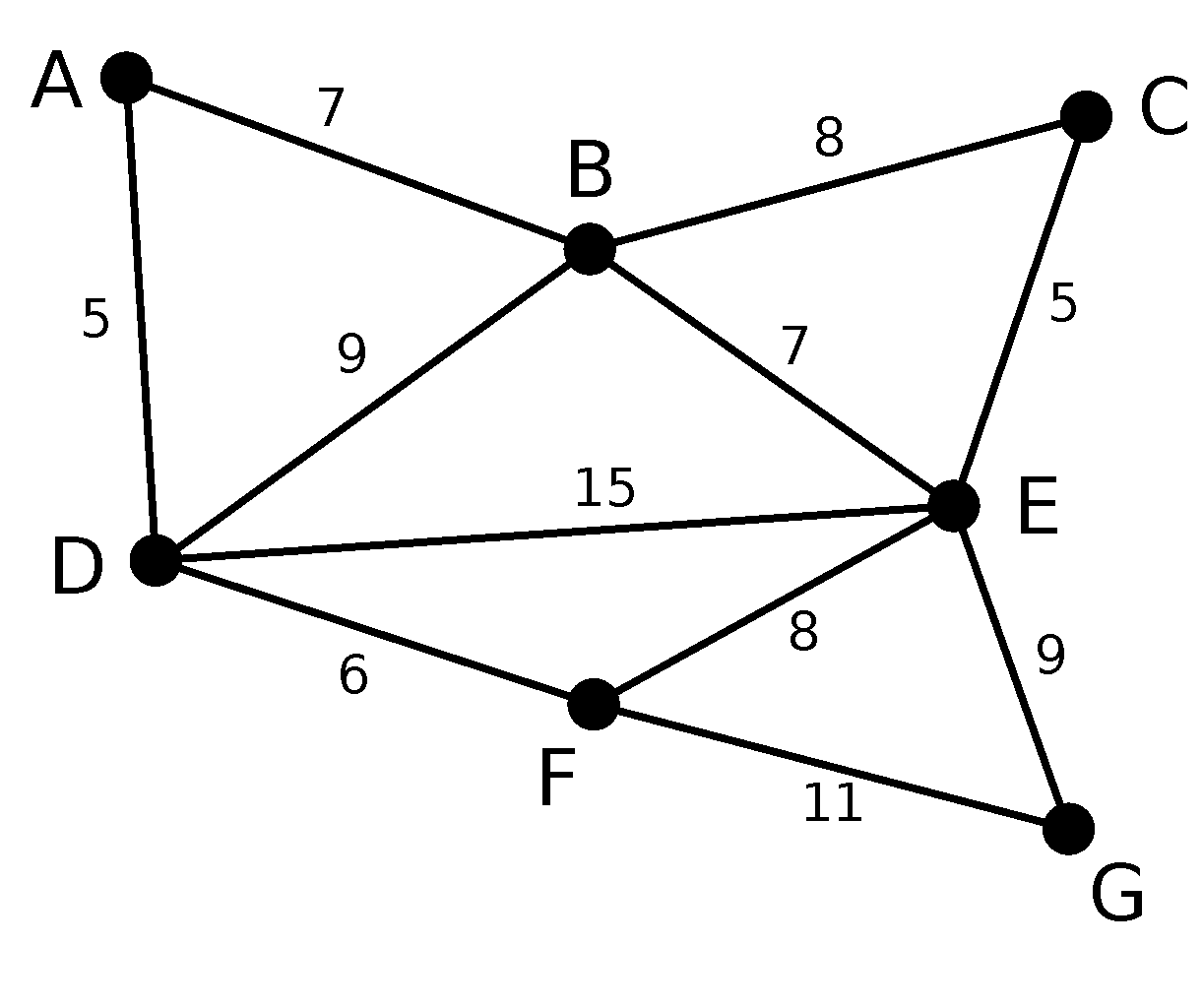
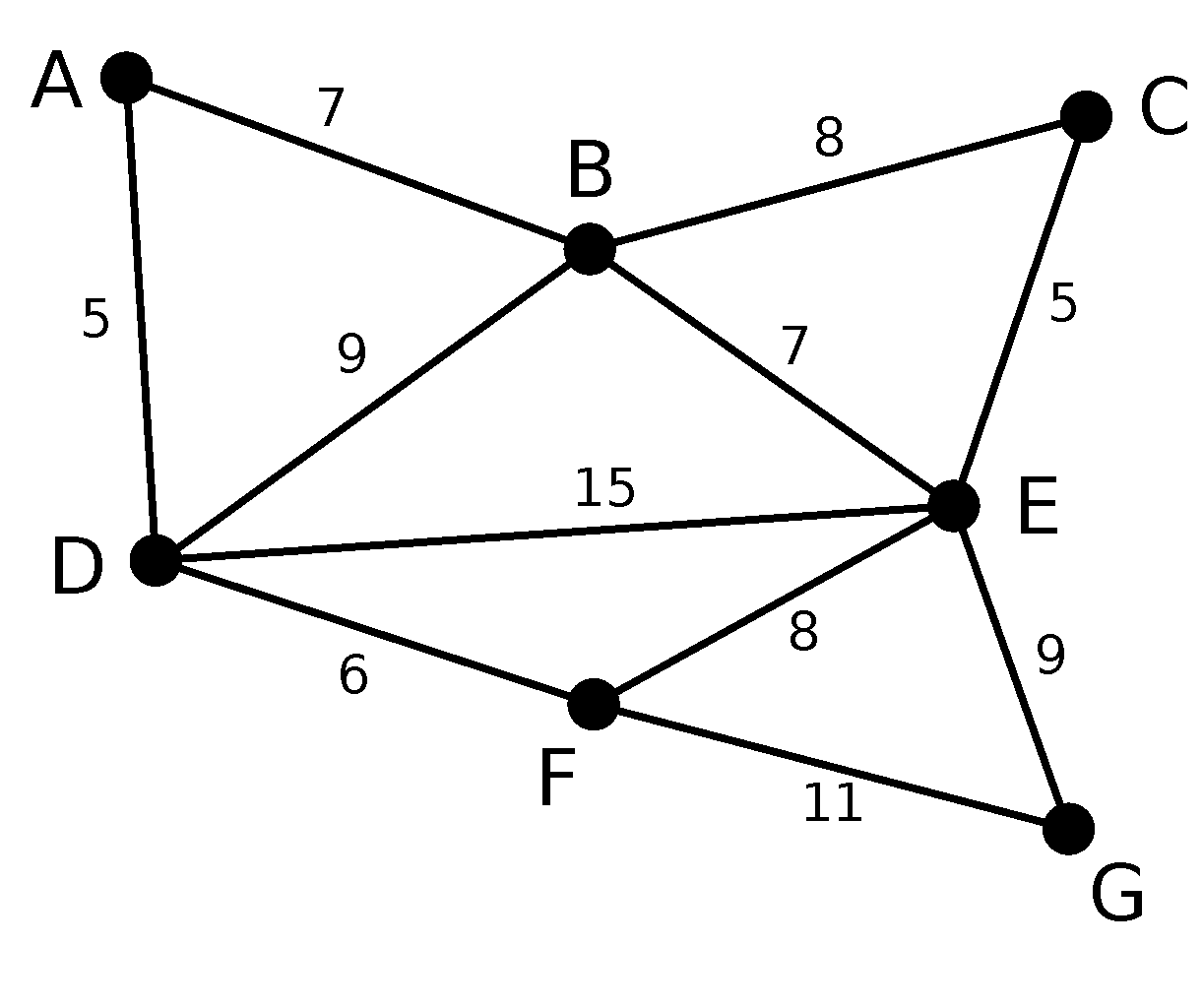
最小生成树

不知不觉，已经是博客园的牢用户了（回归了QAQ）
oi-wiki是个好东西

Kruskal

思路

首先把动图扒下来

一目了然
将边排序，依次加边，看是否已经连接（有点像dij）
排序略，并查集维护集合

实现

//马上写

复杂度

O(m log m),适用于稀疏图

Prim

思路

其实oi-wiki已经讲的很清楚了

跟 Dijkstra 算法一样，每次找到距离最小的一个点，可以暴力找也可以用堆维护。
堆优化的方式类似 Dijkstra 的堆优化，但如果使用二叉堆等不支持 O(1) decrease-key 的堆，复杂度就不优于 Kruskal，常数也比 Kruskal 大。所以，一般情况下都使用 Kruskal 算法，在稠密图尤其是完全图上，暴力 Prim 的复杂度比 Kruskal 优，但 不一定 实际跑得更快。
原来学了dij后世界如此简单

实现

暴力

//马上写

二叉堆

//我懒，把oi-wiki上的扒下来了
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
constexpr int N = 5050, M = 2e5 + 10;

struct E {
  int v, w, x;
} e[M * 2];

int n, m, h[N], cnte;

void adde(int u, int v, int w) { e[++cnte] = E{v, w, h[u]}, h[u] = cnte; }

struct S {
  int u, d;
};

bool operator<(const S &x, const S &y) { return x.d > y.d; }

priority_queue<S> q;
int dis[N];
bool vis[N];

int res = 0, cnt = 0;

void Prim() {
  memset(dis, 0x3f, sizeof(dis));
  dis[1] = 0;
  q.push({1, 0});
  while (!q.empty()) {
    if (cnt >= n) break;
    int u = q.top().u, d = q.top().d;
    q.pop();
    if (vis[u]) continue;
    vis[u] = true;
    ++cnt;
    res += d;
    for (int i = h[u]; i; i = e[i].x) {
      int v = e[i].v, w = e[i].w;
      if (w < dis[v]) {
        dis[v] = w, q.push({v, w});
      }
    }
  }
}

int main() {
  cin >> n >> m;
  for (int i = 1, u, v, w; i <= m; ++i) {
    cin >> u >> v >> w, adde(u, v, w), adde(v, u, w);
  }
  Prim();
  if (cnt == n)
    cout << res;
  else
    cout << "No MST.";
  return 0;
}

Fib堆？

还是算了吧

复杂度

暴力：O(n²+m)。
二叉堆：O((n+m) log n)。
Fib 堆：O(n log n + m)。
一句话：稠密跑Prim，稀疏跑Kruskal

Boruvka

比前面两个难但有优势，所以自己看

次小生成树就不写了