最小费用最大流

终于把自己搞蒙了
简而言之，最小费用最大流就是这样：
图论中的一种理论与方法，研究网络上的一类最优化问题 。很多系统中涉及流量问题，例如公路系统中车流量，网络中的数据信息流，供油管道的油流量等。我们可以将有向图进一步理解为“流网络”(flow network)，并利用这样的抽象模型求解有关流量的问题。
显然我是完全没看懂的，那么，比如我们有一个交通网络如下图。
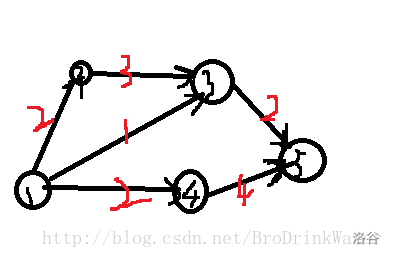边上标的是可以通过的人。
现在我们要从1到5，最多有几个人？
如图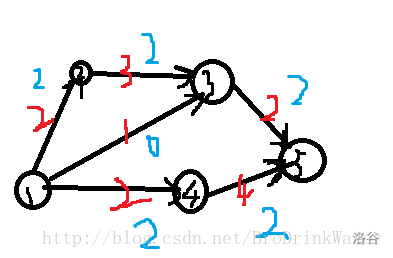：得出最多4人
这就是最大流。
那么，怎么求最大流呢？
求解网络流的基本思想就是每次寻找增广路(就是源点到汇点的一条可行路)然后ans+=增广路能流过的流量，更新剩余网络，然后再做增广路，直到做不出增广路。关于网络流入门最难理解的地方就是剩余网络了....为什么在找到一条增广路后...不仅要将每条边的可行流量减去增广路能流过的流量...还要将每条边的反向弧加上增广路能流过的流量.?..原因是在做增广路时可能会阻塞后面的增广路...或者说做增广路本来是有个顺序才能找完最大流的.....但我们是任意找的...为了修正...就每次将流量加在了反向弧上...让后面的流能够进行自我调整...剩余网络的更新(就在原图上更新就可以了)
（what？speak earth language！）反正我是没看懂的……..若有大神围观勿喷。
接下来蒟蒻给你们讲讲网络流最大流最简单也是最慢的一种EK算法：
我们设刚刚那个啥交通网络为图G，这个图是个有向图，不然做不了,记住这句话，后面有题目。
定义c函数为管道容量大小，就是火车上最多坐多少个人，f函数为管道的流量，就是火车身上现在做了几个人。
显然c函数要大于等于f函数的大小（不多说，水流多了管子会爆，其次，这是中国，不是印度，还是不能坐火车顶上的）。
这是图G的三个性质之一：容量限制，然后有个反对称性，就是流过去的f = 流回来的-f，
现在不懂没事，一会讲反向边的时候细讲，
第三个就是流守恒性，就是从源点出发的总流量等于到汇点的总流量，就是从1出发的人不能在火车上失踪了。
明白了这些，我现在来讲网络流中最难理解的东西：反向边
来个经典的图：

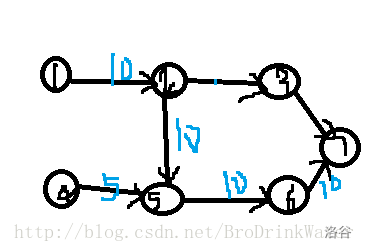
嗯，有向图吧，不多说了，初始是0号节点流向一号节点和四号节点（未画出）1->2->5->6->7
流量都是10，我们假设这条路径上都是满流，就是c = f 就是不能再流其他的流了，然后我们设定其他边上也是c = 10,4->5也有5的流量，如果按照EK算法中的bfs来说，为了找到一个最大流，2->3这条边都不会走，可能一开始找瓶颈把4,5入队，但是后面不断调整流量时，流量回被调成10，毕竟程序是为了寻找最大流，
所以说如果不把流过的边加上一个反向边4->5这个流量都不会被加入增广路，可能你还是没怎么理解，我先来介绍下残量网络，这样你会理解的更深。

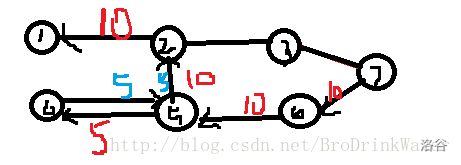
红色的数字代表回流的量，2->3那条边我先暂时不标，在残留网络的中如果那么就给它连一条回去的边，先别问我为什么，慢慢来。连回去的边大小为增广路上流量的大小，原来的边为c-f，流量为0的边不在残量网络中出现。现在我们再来讲讲反相边到底是用来干嘛的，你看，如果给2->5加一条反相边，是不是4可以通过反相边到达汇点7，而原来的图是不行的因为5,6这条边已经满流，所以说，如果不加反相边，会有一条路都找不到，那不就很尴尬了，^_。换句话说，加条反相边那就是给程序一个反悔的机会，现实中，反相边是不存在的，只是在程序中出现，实际上，这就相当于4->5的流量转给2->3，第一条路变成1,2,3,7，第二条路变成4,5,6,7，所以，是不是更好理解了呢？接下来，我来讲讲EK的代码。

//不要太在意代码风格啦。
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<iostream>
#include<cstdio>
#define For(a,b,c) for(a=b;a<=c;a++)
#include<queue>
#define inf 999999999
using namespace std;
const int maxn = 1010;
int rong[510][510],liu[510][510];
int p[maxn];
int m,n;
int pre[maxn];
int sum;
void internet() {
	queue<int> q;
	while(1) { //不断通过bfs来找增光路，然后ans+=增光路上的流量。
		int i,j;
		memset(p,0,sizeof(p));
		p[1]=inf;//这里的p数组有两个作用，一是用来标记是非访问过，其次是用来记增广路上的瓶颈。
		q.push(1);
		while(!q.empty()) {
			int ans=q.front();
			q.pop();
			For(i,1,n) {
				if(!p[i]&&liu[ans][i]<rong[ans][i]) {
					p[i]=min(p[ans],rong[ans][i]-liu[ans][i]);
					pre[i]=ans;//记录增广路。
					q.push(i);
				}
			}
		}
		if(!p[n]) {
			break;//如果n点找不到增光路，说明已经没增广路到汇点了。
		}
		sum+=p[n];
		int tmp=n;
		while(pre[tmp]) { //不断调整流量大小。
			liu[pre[tmp]][tmp]+=p[n];
			liu[tmp][pre[tmp]]-=p[n];
			tmp=pre[tmp];
		}
	}
}
int main() {
	int i,j,k;
	int x,y,z;
	while(scanf("%d%d",&m,&n)!=EOF) {
		sum=0;
		memset(pre,0,sizeof(pre));
		memset(rong,0,sizeof(rong));
		memset(liu,0,sizeof(liu));
		For(i,1,m) {
			scanf("%d%d%d",&x,&y,&z);
			rong[x][y]+=z;
		}
		internet();
		printf("%d\n",sum);
	}
	return 0;
}

嗯，EK，还是很简单的，接下来我们讲讲dinic。dinik是啥捏，就是比EK快的算法，跟二分图匹配里的hk算法很像。显然我还是不知道！！！dinic用到了一个深度标号，是bfs求得的，根据bfs的性质，标号大小是按距离远近严格递增的，搜索树中同一层的为同一标号，如图，蓝色数字为深度标号

很形象是吧，bfs都不会的话，那还是先别碰网络流，然后我们按照深度标号严格递增或递减（看是从源点还是汇点出发）用dfs搜索，然后就好了。那为什么？因为之前讲反向边的时候我将讲过，实际上1到5的路径中，我们现实中肉眼观察只有1,2,5，和1,3,5这两条边中间的边是不会流的，因为时加入的反向边，时间上不存在，如是我们就可以按照标号严格递增或递减来进行搜素，然后松弛即可。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
#define REP(i,a,b) for(register int i = (a), i##_end_ = (b); i <= i##_end_; ++i)inline int read() {
register int c = getchar(), fg = 1, sum = 0;
while(c > '9' || c < '0' ) {
	if(c == '-')fg = -1;
	c = getchar();
}
while(c <= '9' && c >= '0') {
	sum = sum *10 + c - '0';
	c = getchar();
}
return fg * sum;
}
const int maxn = 1010;
int n,m;
int be[maxn], ne[maxn], to[maxn], e = 0, w[maxn];
int d[maxn];
void add(int x,int y,int z) {
	to[e] = y;
	ne[e] = be[x];
	be[x] = e;
	w[e] = z;
	e++;
}
int bfs() {
	memset(d,-1,sizeof(d));
	queue<int>q;
	q.push(n),d[n] = 0;
	while(!q.empty()) {
		int u = q.front();
		q.pop();//这里为什么是i！=-1呢？因为，标号是从0开始的
		for(int i = be[u]; i!=-1; i = ne[i]) {
			int v = to[i];//这里的^是很常用的，因为前向星加边是两条一起加的，只是反向边一开始是为零的，所以^1一下可以得到另一条边，比如0^1 = 1,1 ^ 1 = 0, 2^1 = 3,3 ^1 = 2;
			if(w[i ^ 1] && d[v] == -1) {
				d[v] = d[u] + 1;
				q.push(v);
			}
		}
	}
	return d[1] != -1 ;
}
int dfs(int x,int low) {
	if(x == n)return low;//low为瓶颈。
	int k;
	for(int i = be[x]; i!=-1 ; i = ne[i]) {
		int v = to[i];
		if(w[i] && d[v] == d[x] - 1 ) {
			k = dfs(v,min(low,w[i]));
			if(k>0) {
				w[i] -= k;
				w[i^1] += k;
				return k;
			}
		}
	}
	return 0;
}
int main() {
	while(scanf("%d%d",&m,&n)!=EOF) {
		e = 0;
		memset(be,-1,sizeof(be));
		REP(i,1,m) {
			int x,y,z;
			x = read(), y = read(), z = read();
			add(x,y,z);
			add(y,x,0);
		}
		int ans = 0,k;
		while(bfs()) {
			k = dfs(1,1e7);
			ans += k;
		}
		printf("%d\n",ans);
	}
}

三：费用流
这里只讲最小费用流，只是讲EK中的bfs换成了spfa，因为网络中的每条边有了个费用。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
#define REP(i, a, b) for(register int i = (a), i##_end_ = (b); i <= i##_end_; ++ i)#define DREP(i, a, b) for(register int i = (a), i##_end_ = (b); i >= i##_end_; -- i)#define mem(a, b) memset((a), b, sizeof(a))#define inf 999999999int read() {
int sum = 0, fg = 1;
char c = getchar();
while(c < '0' || c > '9') {
	if (c == '-') fg = -1;
	c = getchar();
}
while(c >= '0' && c <= '9') {
	sum = sum * 10 + c - '0';
	c = getchar();
}
return sum * fg;
}
int n,m,num1 = 0,num2 = 0;
int be[100010], ne[100010], to[100010], c[100010], w[100010], e;
char s[200];
int pre[20010],id[20010],p[20010],d[20010];
struct T {
	int x,y;
} H[10010],hm[10010];
void add(int x,int y,int ci,int wi) {
	to[e] = y;
	ne[e] = be[x];
	be[x] = e;
	c[e] = ci;
	w[e] = wi;
	e++;
	to[e] = x;
	ne[e] = be[y];
	be[y] = e;
	c[e] = 0;
	w[e] = -wi;
	e++;
}
bool spfa() {
	queue<int>q;
	REP(i,0,num1+num2+1)d[i] = inf;
	memset(pre,-1,sizeof(pre));
	memset(id,-1,sizeof(id));
	memset(p,0,sizeof(p));
	q.push(0),d[0] = 0, p[0] = 1;
	while(!q.empty()) {
		int u = q.front();
		q.pop();
		p[u] = 0;
		for(int i = be[u]; i != -1 ; i = ne[i]) {
			int v = to[i];
			if(c[i]) {
				if(d[v] > d[u] + w[i]) {
					d[v] = d[u] + w[i];
					pre[v] = u;
					id[v] = i;
					if(!p[v]) {
						q.push(v);
						p[v] = 1;
					}
				}
			}
		}
	}
	return d[num1+num2+1] < inf;
}
int calc() {
	int sum = 0, flow = inf;
	for(int i = num1+num2+1; pre[i]!= -1; i = pre[i])flow = min(flow, c[id[i]]);
	for(int i = num1+num2+1; pre[i]!= -1; i = pre[i]) {
		sum+=w[id[i]] * flow;
		c[id[i]] -= flow;
		c[id[i] ^ 1] += flow;
	}
	return sum;
}
int main() {
	while(1) {
		n = read(), m = read();
		if(n == 0 && m == 0)break;
		memset(H,0,sizeof(H));
		memset(hm,0,sizeof(hm));
		memset(be,-1,sizeof(be));
		e = 0;
		num1 = num2 =0;
		REP(i,1,n) {
			scanf("%s",s);
			REP(j, 0, strlen(s) - 1) {
				if(s[j] == 'H')H[++num1].x = i, H[num1].y = j+1;
				if(s[j] == 'm')hm[++num2].x = i,hm[num2].y = j+1;
			}
		}
		REP(i, 1, num1)REP(j,1,num2) {
			int k = abs(H[i].x-hm[j].x)+abs(H[i].y-hm[j].y);
			add(i,j+num1,1,k);
		}
		REP(i, 1, num1)add(0,i,1,0);
		int k = num1 + num2 + 1;
		REP(i,num1+1,num1+num2)add(i,k,1,0);
		int ans = 0;
		while(spfa())ans += calc();
		printf("%d\n",ans);
	}
	return 0;
}

一个模板，提供借鉴。今后几天我会发几篇网络流好题的blog，希望大家看了有所收获。
yuan