NLP与深度学习（二）循环神经网络

1. 循环神经网络

在介绍循环神经网络之前，我们先考虑一个大家阅读文章的场景。一般在阅读一个句子时，我们是一个字或是一个词的阅读，而在阅读的同时，我们能够记住前几个词或是前几句的内容。这样我们便能理解整个句子或是段落所表达的内容。循环神经网络便是采用的与此同样的原理。

循环神经网络（RNN，Recurrent Neural Network）与其他如全连接神经网络、卷积神经网络相比，最大的特点在于：它的内部保存了一个状态，其中包含了与已经查看过的内容的相关信息。

下面便先以SimpleRNN为例，介绍这一特点。

2. SimpleRNN

SimpleRNN的结构图如下所示：

Fig. 1. ShusenWang. Simple RNN 模型^[2]

可以看到，SimpleRNN的模型比较简单，在t时刻的输出，等于t-1 时刻的状态h_t-1与t时刻的输入X_t的集成。

用公式表示为：

output_t = tanh( (W * X_t) + (U * h_t-1) + bias )

其中W为输入数据X的参数矩阵，U为上一状态 h_t-1的参数矩阵。且这2个参数矩阵全局共享（也就是说，每个时间步t的W与U矩阵都相同）。

举个例子，如图中的文本序列：the cat sat on the mat。假设输入只有这单个序列，则输入SimpleRNN时，输入维度为(1, 6, 32)。这里1对应的是batch_size（RN也和其他神经网络一样，可以接收batch数据），6对应的是timesteps（也可以理解为序列长度）；32对应的是词向量维度（这里假设词嵌入维度为32维）。所以SimpleRNN的输入参数shape为(batch_size, timesteps, input_features)。

在第一个单词the进入RNN后，会进行第一个状态和输出h₀ 的计算。假设单词the的向量为 X_the，初始化的状态为 h_first（最初始的h_first取全0），则：

h₀ = tanh( (W * X_the) + (U * h_first) + bias)

到输出最后一个状态 h₅ 时（此时输入单词为mat），即为：

h₅ = tanh( (W * X_mat) + (U * h₄) + bias)

最终输出的状态 h₅ 即包含了前面输入的所有状态（也就是整个序列的信息），此输出即可输入到例如Dense层中用于各类序列任务，如情感分析，文本生成等NLP任务中。

在tensorflow中调用SimpleRNN非常简单，下面是一个简单的单个SimpleRNN的例子：

from tensorflow.keras import Sequential
from tensorflow.keras.layers import Embedding, SimpleRNN

model = Sequential()
model.add(Embedding(10000, 64))
model.add(SimpleRNN(32))
model.summary()


Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding (Embedding)        (None, None, 64)          640000    
_________________________________________________________________
simple_rnn (SimpleRNN)       (None, 32)                3104      
=================================================================
Total params: 643,104
Trainable params: 643,104
Non-trainable params: 0
_________________________________________________________________

其中可以看到SimpleRNN层的输出仅为最终状态h_t的维度。

需要注意的是，给SimpleRNN的参数，我们给的是32。这里可能刚接触SimpleRNN时容易弄混的一点是：参数32并非是时间步长数，而是SimpleRNN的输出维度，也就是h_t的维度。

还有之前遇到过的一个问题是：在SimpleRNN中，第一层Embedding的输出为64，第二层的输出为32 是如何计算得出的？

对于这个问题，我们看一下这个例子中SimpleRNN层的参数shape：

for w in model.layers[1].get_weights():
    print(w.shape)

(64, 32)
(32, 32)
(32,)

从输出可以看到，这层SimpleRNN有3个参数，分别对应的就是前面提到的公式W，U与bias。在Embedding层的输出经过了与第一个参数W的矩阵运算后，输出即转换为了32维度。

3. RNN

上面提到的SimpleRNN之所以叫SimpleRNN，是因为它相对于普通RNN做了部分简化。实际上SimpleRNN并非是原始RNN。为了避免读者对这2个模型产生混淆，下面简单介绍RNN。

RNN与SimpleRNN的最大区别在于：SimpleRNN少了一个输出计算步骤。下面是2者的对比：

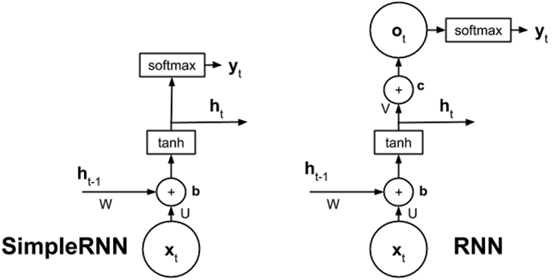
Fig. 2. Rowel Atienza. Introucing Advanced Deep Learning with Keras^[3]

可以看到在，在计算得到timestep t时刻的状态h_t后，相对于SimpleRNN立即将h_t输出到softmax（此处的softmax层并非属于RNN/SimpleRNN里的结构），RNN还对输出进行了进一步处理 o_t = V*ht + c，然后再输出到下一步的softmax中。

4. SimpleRNN的局限性

前面我们介绍了SimpleRNN可以用于处理序列（或是时序数据），其中每个timestep t 的输出状态h_t包含了t时刻前的所有输入信息。

但是，SimpleRNN有它的局限性：管理长序列的能力有限。对于长序列，使用SimpleRNN时会带来2个问题：

梯度爆炸&消失问题：随着序列的长度增长，在反向传播更新参数的过程中，越靠近顶层的梯度会越来越小。这样便会导致网络的训练速度变慢，甚至时无法学习。本质上是由于网络层数增加后，反向传播中梯度连乘效应导致；
忘记最早的输入信息：同样，随着序列长度的增加，在最终输出时，越靠近顶部的单词对最终输出状态h_t的占比会越来越小。此原因也是由于参数U的连乘导致的。

由于SimpleRNN对处理长序列的局限性，后续又提出了更高级的循环层：LSTM与GRU。这2个层都是为了解决SimpleRNN所存在的问题而提出。

5. LSTM

LSTM（Long short-term memory）称为长短记忆，由Hochreiter和Schmidhuber在1997年提出。当今仍在被使用在各类NLP任务中。下面是LSTM的结构图：

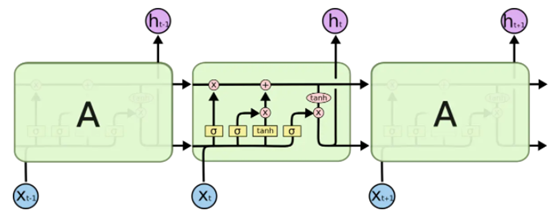
Fig. 3. colah. Understanding LSTM Networks^[4]

LSTM也属于RNN中的一种，所以它的输入数据也是时序或序列数据。同样，它在t时间步的输入也是X_t，输出为状态h_t。但是它的结果比SimpleRNN要复杂的多，有4个参数矩阵。它最重要的设计是一个传输带向量C（也称为Cell或Carry）：

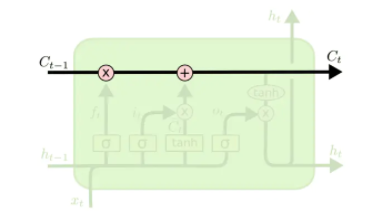
过去的信息可以通过传输带向量C送到下一个时刻，并且不会发生太大的变化（仅有上图中的乘法与加法2种线性变换）。LSTM就是通过传输带来避免梯度消失的问题。

在LSTM中，有几种类型的门（Gate），用于控制传输带向量C的状态。下面分别介绍这几个Gate，以及输出状态的计算方式。

5.1. Forget Gate

Forget Gate 称为遗忘门，结构如下：

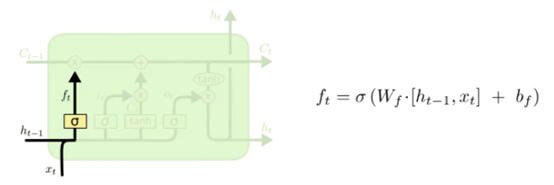
从上图可以看出，遗忘门是将输入x_t与上一个状态h_t-1 进行concatenate合并后，与Forget Gate参数矩阵W_f进行矩阵乘法，加上偏移量b_f。经过激活函数sigmoid函数进行处理，得出f_t。

由于f_t为sigmoid函数的结果，所以它的每个元素范围均为(0,1)。举个例子，假设a = W_f * [h_t-1, x_t] + b_f，且a的结果为[1, 3, 0, -2]，则经过softmax后，f_t为：

import tensorflow as tf
import numpy as np

a = np.array([[1., 3., 0., -2.]])
a = tf.convert_to_tensor(x)

f_t = tf.keras.activations.softmax(x)
f_t.numpy()

array([[0.73105858, 0.95257413, 0.5, 0.11920292]])

然后f_t会与传输带向量C_t-1做元素级乘法。举个例子，假设C_t-1向量为[0.9, 0.2, -0.5, -0.1]，f_t向量为[0.5, 0, 1, 0.8]，则它们的乘积为：

Output = [ (0.9 * 0.5), (0.2 * 0), (-0.5 * 1), (-0.1 * 0.8) ] = [0.45, 0, -0.5, -0.08]

很明显可以看出，遗忘门f_t向量对传输带向量Ct的信息进行了过滤：

对于f_t中数值为1的元素，可以让对应C_t-1位置上的元素通过（如Output中的第3个元素，其值与C_t-1中的值一致）
对于f_t中数值为0的元素，可以让对应C_t-1位置上的元素不能通过（如Output中的第2个元素，其值为0）
对于f_t中数值为 (0, 1) 范围的元素，可以让对应C_t-1位置上的元素部分通过（如Output中的第1个元素与第4个元素，其值分别为C_t-1中值的50%与80%）

这样Forget Gate便对传输带向量C进行了信息过滤，也可以说决定了传输带向量C需要遗忘的信息。

5.2. Input Gate

下一步需要决定的是：什么样的新信息被存放在传输带向量C中。这里引入了另一个门，称为输入门（Input Gate）。

这一步的过程图如下：

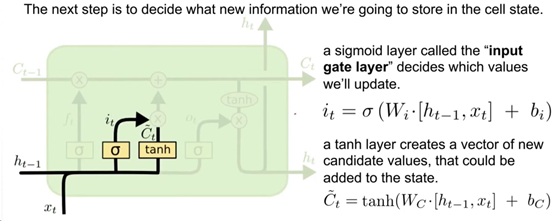
可以看到这里出现了2个新的向量i_t与C^~_t。需要注意的是，Input gate仅代表i_t。

Input Gate 的输出i_t 与前面的Forget Gate中f_t的计算方法一模一样，可以理解为最终也是起到一个过滤的作用。

C^~_t的计算也与i_t基本一样，不同的是，激活函数由sigmoid替换为了tanh。由于使用了tanh，所以C^~_t向量中所有元素都位于(-1, 1) 之间。

5.3. 更新传输带向量C

在计算得出了f_t，i_t与C^~_t后，便可更新传输带向量C_t的值。更新过程如下图所示：

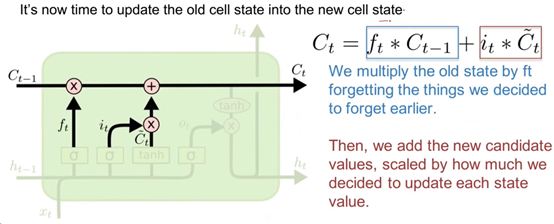
更新过程分为2部分，第1部分是遗忘门f_t部分，前面在介绍Forget Gate的作用时已经进行了描述，在此不再阐述。

第2部分为i_t * C^~_t，前面Input Gate中提到的作用i_t也类似与对信息进行过滤，而C^~_t也是输入信息x_t与上一状态h_t-1的另一种整合方法。这2个向量进行矩阵点乘后，将结果数据通过矩阵加法的运算，添加到第1部分的输出中，便得到了t时刻的传输带向量C_t的值。

简单地说，C_t就是先通过遗忘门f_t忘记了C_t-1中的部分信息，然后又添加了来自Input Gate中部分新的信息。

5.4. Output Gate

在更新完传输带向量C_t后，下一步便是计算t时刻的状态h_t，这个过程中引入了最后一个门，称为输出门（Output Gate）。

最后输出h_t的计算过程如下图所示：

从图中我们可以看到，Output Gate的输出o_t的计算方式与Forget Gate、Input Gate的计算方式完全一样。

输出门o_t向量由于经过了sigmoid函数，所以其所有元素的范围均在(0, 1) 之间。

最后在计算h_t时，先对传输带向量C_t做tanh变换，这样其结果中每个元素的范围便均在(-1, 1) 之间。然后使用输出门o_t向量与此结果做矩阵点乘，便得到t时刻的状态输出h_t。

h_t会有2个副本，1个副本用于输出，另1个副本用于输入到下一个时间步t+1中，作为输入。

5.5. LSTM总结

LSTM与SimpleRNN最大的区别在于：LSTM使用了一个“传输带“，可以让过去的信息更容易地传输到下一时刻，这样便使得LSTM对序列的记忆更长。从实际使用上来看，LSTM的效果基本都是优于SimpleRNN。

对于LSTM中3个门的进一步理解，在《Deep Learning with Python》^[1]这本书中，作者Francois Chollet提到了非常好的一点：对于这些门的解释，例如遗忘门用于遗忘传输带向量C中的部分信息，输入门用于决定多少信息输入到传输带向量C中等。对于这些门的功能解释并没有多大意义。因为这些运算的实际效果，是由参数权重决定的。而参数权重矩阵每次都是以训练的方式，从端到端中学习而来，每次训练都需要从头开始，所以不可能为某个运算赋予特定的目的。所以，对RNN中的各类运算组合，最好是将其解释为对参数搜索的一组约束，而非是出于工程意义上的一种设计。

前面介绍过，在解决SimpleRNN的问题时，除了LSTM，还有另一种模型称为GRUs（Gated recurrent units）。GRUs也是引入了Gate的概念，不过相对与LSTM来说更简单，门也更少。

在实际应用中，大部分场景还是会使用LSTM，而非GRUs。所以本文不会再具体介绍GRUs。

6. Stacked RNN

与其他常规神经网络层一样，RNN的网络也可以进行堆叠。前面我们介绍SimpleRNN时，提到它的输出仅为最终的h_t向量，但是RNN的输入是一个序列，无法直接将单个 h_t向量输入到RNN中。

在这种情况下，对RNN进行堆叠，就需要每个时间步t的输出，如[h₀, h₁, h₂, …, h_t]，然后将这些状态h，作为下一层RNN的输入即可。如下图所示：

Fig. 5. Deep RecurrentNeuralNetworks^[5]

在keras中实现的方式也非常简单，指定RNN的return_sequences=True参数即可（最后一层RNN不指定），如下所示：

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Embedding, Dense

vocabulary = 10000
embedding_dim = 32
word_num = 500
state_dim = 32

model = Sequential([
    Embedding(vocabulary, embedding_dim, input_length=word_num),
    LSTM(state_dim, return_sequences=True, dropout=0.2),
    LSTM(state_dim, return_sequences=True, dropout=0.2),
    LSTM(state_dim, return_sequences=False, dropout=0.2),
    Dense(1, activation='sigmoid')
])

7. 双向RNN网络

前面我们看到的SimpleRNN，LSTM都是从左往右，单向地处理序列。在NLP任务中，还常常用到双向RNN。双向RNN是RNN的一个变体，在某些任务上比单向RNN性能更好。

在机器学习中，如果一种数据的表示方式不同，但是数据是有价值的话，则是非常值得探索不同的表示方式。若是这种表示方式的差异越大则越好，因为它们提供了其他查看数据的角度，从而获取数据数据中被其他方法所忽略的信息。这个便是集成（ensembling）方法背后的直觉。在图像识别任务中，数据增强的方法也是基于这一理念。

双向RNN的示例图如下所示：

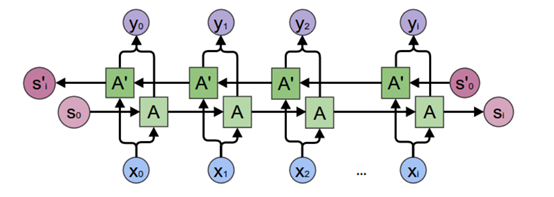
Fig. 6. Colah, Neural Networks, Types, and Functional Programming^[6]

从上图中，我们可以看到，双向神经网络是分别从2个方向（从左到右，从右到左），独立地训练了2个神经网络。输入数据均为X。在得到2个神经网络的输出状态h_left, h_right后，再将2个向量进行拼接（concatenate）操作，即得到了输出向量y。这个输出向量y [y₀, y₁, y₂,… y_i] 即可输入到下一层RNN中。

若是仅需要类似SimpleRNN中h_t的单个输出，则将y向量丢弃，仅将s_i 与s’_I 做拼接后输出即可。

在keras中，实现双向RNN的网络也非常简单，仅需要将layer用Bidirectional() 方法进行包装即可。例如：

# Bidirectional LSTM

vocabulary = 10000
embedding_dim = 32
word_num = 500
state_dim = 32

from tensorflow.keras.layers import Bidirectional

model_blstm = Sequential([
    Embedding(vocabulary, embedding_dim, input_length=word_num),
    Bidirectional(LSTM(state_dim, return_sequences=False, dropout=0.2)),
    Dense(1, activation='sigmoid')
])

model_blstm.summary()

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_1 (Embedding)      (None, 500, 32)           320000    
_________________________________________________________________
bidirectional (Bidirectional (None, 64)                16640     
_________________________________________________________________
dense_1 (Dense)              (None, 1)                 65        
=================================================================
Total params: 336,705
Trainable params: 336,705
Non-trainable params: 0