降维(三)LLE与其他降维技术
LLE
局部线性嵌入,Locally Linear Embedding(LLE)是另一个功能强大的非线性降维(nonlinear dimensional reduction,NLDR)技术。它是一个流形学习技术,并不基于投影。简单地说,LLE工作的方式是:首先衡量每个训练实例与它最近的邻居们(closest neighbors,c.n.)的线性相关程度,然后在这些局部关系可以得到最好地保存的情况下,寻找一个低维的表示训练集的方式。这个方法在展开弯曲的流形时非常有用,特别是数据集中没有太多的噪点时。
下面的代码使用sk-learn的LocallyLinearEmbedding类将一个瑞士卷展开:
from sklearn.manifold import LocallyLinearEmbedding lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10) X_reduced = lle.fit_transform(X)
生成的2D数据集结果如下图所示:
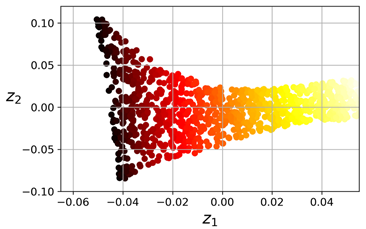
我们可以看到,瑞士卷被完全地展开了,并且实例之间的距离非常好地在局部保持了。不过,在更大的规模层面上,距离并没有保持好:左边部分的瑞士卷是伸展的,而右边的部分是紧缩的。尽管如此,LLE在流形建模中仍表现的非常好。
LLE的具体工作方式为:对于每条训练实例x(i),算法识别它的k个最邻近邻居(在上面的代码中k=10),然后尝试用它的这些邻居以一个线性函数的方式重构x(i)。更具体地说,它会找到一组权重wi,j使得x(i)与∑wi,jx(j)(其中j 初始为1,累加到第m)之间的平方距离尽可能的小,如果x(j)并不是x(i)的最近k个邻居之一,则假设wi,j = 0。所以LLE的第一步是下面的带约束优化问题,这里W是权重矩阵,包含所有的权重wi,j。第二个约束是对每个训练实例x(i)的权重们一个简单的标准化约束:

在这个步骤完成后,权重矩阵Wˆ(包含权重wˆi,j)便对训练实例之间的局部线性关系进行了编码。第二个步骤就是将训练实例映射到一个d维的空间中(d < n),同时尽可能地保留这些局部关系。如果z(i)是x(i)在这个d维空间里的像(image),则我们会想要z(i)与∑wˆi,jz(j) (其中j初始为1,累加到第m)之间的平方距离尽可能的小。这个想法便产生了下一个带约束的优化问题(如下公式所示)。它与第一个步骤非常像,但是并不是固定实例然后找到最优的权重,而是做相反的事情:保持权重固定,在低维空间中找到实例的image的最优位置。需要主要的是,这里Z是包含了所有z(i)的矩阵。
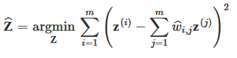
sk-learn的LLE实现,它的计算复杂度,找到k个最近邻居的复杂度是O(m log(m)n log(k)),优化权重的复杂度是O(mnk3),以及构造低维空间表示的复杂度是O(dm2)。可惜的是,在最后一个公式中m2的会让这个算法对超大数据集的扩展十分糟糕。
其他降维技术
还有很多种其他的降维技术,其中部分有在sk-learn中提供,下面是最热门的几个:
- 随机投影
- 如它名称所示,使用一个随机的线性投影,将数据投影到一个低维空间中。这个听起来很奇怪,不过结果证明,这种随机投影实际上几乎可以很好的保留距离。它的降维质量取决于数据的条目以及目标label的维度,而却不是初始的维度。可以查看sklearn.random_projection 包获取更多信息
- 多维缩放(Multidimensional Scaling,MDS)
- 在尽量保持实例之间距离的情况下减少维度
- Isomap
- 通过将每个实例与它的最近邻居连接起来,而创建一个图。然后在尽量保持实例之间测地距离(geodesic distances)的情况下减少维度
- t-分布式随机邻居嵌入(t-Distributed Stochastic Neighbor Embedding(t-SNE)
- 在保持相似实例接近而非相似实例远离的情况下减少维度。它大部分用于数据可视化,特别是在可视化高维空间中的实例簇(clusters of instances)时(例如,将MNIST图片在2D上进行可视化)。
- 线性判别分析(Linear Discriminant Analysi,LDA)
- 它是一个分类算法,不过在训练时,它会学习最能分辨不同类别的判别轴(discriminative axes),然后这些轴可以被用于定义一个超平面,数据之后便可以投影到这个超平面上。这个方法的好处是投影会保持不同类别尽可能的远离,所以LDA是一个很好的降维技术,它可以用于在执行另外的分类算法(如SVM)前进行降维。
下图展示了其中几种技术:






