降维（二）PCA

PCA

主成成分分析（Principal Component Analysis，PCA）在目前是非常热门的降维算法。首先它找到一个最接近数据的超平面，然后将数据投影到这个平面上。

 

保持方差（Preserving the Variance）

在将训练集投影到一个低维超平面之前，我们首先要选择正确的超平面。例如，下图左图是一个简单的2D数据集，伴随有3个不同的轴（也就是1D超平面）。右边是数据集在每个轴上投影后的结果。我们可以看到，在实线上的投影保有最大的方差，而投影到点状线上的结果保有非常低的方差，在虚线上的结果保有中等的方差：

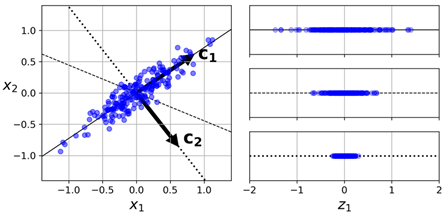
看起来选择那条保有最大方差的轴会比较合理，因为它相对其他轴来说，是最可能丢失更少信息办法。另一个方法是：证明这个选择是使得投影到轴前后的点之间均方误差最小的。这也就是PCA背后的简单思想。

 

主成成分（Principle Components）

PCA会在训练集中找出让方差最大的那些轴，也就是上图中的那条实线。它同时也会找第二个轴，与第一个轴正交的轴。在上面的2D例子中，毫无疑问，它是那个点状线。如果它是一个更高维的数据集，PCA还会找第三个轴，与前两个轴均正交的轴，然后第4个、第5个，依此类推，直到找到与数据集维度相等的轴个数。

第i^th轴称为数据的第i^th主成成分（principal component）。在上图的2D例子中，第一个PC是向量c1 所在的那个轴上，第二个PC是向量c2所在的那个轴。

需要注意的是，对每个主成成分，PCA会找到一个零中心单位向量（zero-centered unit vector）指向PC的方向。由于两个相反的单位向量在同一个轴上，所以PCA返回的单位向量并不是稳定的：如果我们轻微干扰训练集然后再次运行PCA，单位向量可能与原始向量指向的方向相反。不过，它们一般会仍在同样的轴上。在某些情况下，一对单位向量甚至可能旋转或交换（如果与这两个轴对应的方差很接近的话），不过它们定义的平面一般会保持一样。

那，我们如何找到训练集的主成成分呢？幸运的是，有一个标准矩阵分解技术，奇异值分解（Singular Value Decomposition，SVD）可以将训练集X分解为3个矩阵的乘积：U Σ V^⊺。V包含的是我们要找的那些定义了所有主成成分的单位向量，如下公式所示：

下面的Python 代码使用NumPy的svd() 方法，可以获取训练集的所有主成成分，然后提取出两个单位向量，它们定义了前两个PC：

X_centered = X - X.mean(axis=0)

U, s, Vt = np.linalg.svd(X_centered)

c1 = Vt.T[:, 0]

c2 = Vt.T[:, 1]

 

需要注意的是，PCA假设数据集是以原点为中心的。在sk-learn中的PCA类会为我们处理好数据中心化的操作。如果我们自行实现PCA的话（例如上面的例子），或者我们使用其他库的话，千万不要忘了先将数据中心化。

 

投影到d维

在我们找到所有主成成分后，若是我们需要将数据集的维度降到d维，则可以将它投影到前d个主成成分定义的超平面上即可。选择这个超平面可以确保投影保有尽可能大的方差（variance）。

将训练集投影到超平面，并获取数据集降到d维后的X_d-proj数据集时，需要计算训练集矩阵X与矩阵W_d的乘积，W_d代表的是V矩阵中前d列的矩阵。如下公式所示：

Xd-proj=XWd

 

下面的python代码将训练集投影到由两个主成成分定义的平面上：

W2 = Vt.T[:, :2]

X2D = X_centered.dot(W2)

 

使用sk-learn

Sk-learn的PCA类使用SVD分解实现 PCA，与我们前面提到的类似。下面的代码应用PCA对数据及降维到2维（需要注意的是，它自动处理了数据中心化）：

from sklearn.decomposition import PCA

 

pca = PCA(n_components=2)

X2D = pca.fit_transform(X)

 

在将PCA transformer 应用到数据集后，它的components_ 属性会包含的W_d转置（例如，定义了第一个主成成分的单位向量等同于pca.components_.T[:, 0]）。

 

Explained Variance Ratio

另一个非常有用的信息是每个主成成分的解释方差比（explained variance ratio），可以通过explained_variance_ratio_ 变量获取。这个比率表示的是数据集的方差沿着每个主成成分上的占比。例如，我们以一个3D数据集为例，它的前两个主成成分的explained variance ratio 为：

pca.explained_variance_ratio_

array([0.84248607, 0.14631839])

 

这个结果告诉我们，84.2% 的数据集方差（variance）落在第一个PC，14.6% 落在第二个PC。这个还给第三个PC留下了少于1.2% 的方差，所以我们可以很合理地假设第3个PC可能并没有携带多少信息。

 

选择正确的维度数

在选择维度数时，不是随便选，而是选择使得explained variance ratio总和足够大（例如95%）的维度数。除非我们是要做数据可视化，这种情况下，我们会将维度降维到2或3。

下面的代码执行PCA，但不进行降维，然后计算最小维度数，使得它能保留训练集方差的95%以上：

pca = PCA()

pca.fit(X_train)

cumsum = np.cumsum(pca.explained_variance_ratio_)

d = np.argmax(cumsum >= 0.95) + 1

 

然后我们可以设置 n_components=d，并再次执行PCA。不过有一个更好的选项：不设置保留的主成成分数，而是设置n_components 为一个0.0到1.0之间的float值，表示的是我们希望保留的variance ratio量：

pca = PCA(n_components=0.95)

X_reduced = pca.fit_transform(X_train)

 

还有另一个选项是画出explained variance对维度数的图（直接画出cumsum即可，如下图所示）。一般它都是一个弓形图，explained variance会先快速增长，之后便停止快速增长，我们选择停止快速增长的那个点即可。在这个例子中，我们可以看到将维度降到100时，不会损失太多的explained variance。

 

PCA 与压缩

在执行降维后，训练集会占据更少的空间。例如，如果对MNIST数据集应用PCA，且保留95%的方差。则我们会看到每个实例将会仅有150个特征，而不是之前的784个特征。所以，在保留有大部分的方差的情况下，数据集现在仅有低于20%原有数据集的大小。这个是一个非常好的压缩比，并且我们也可以看到这种数量的减少极大地增加了分类算法的速度（例如SVM分类器）。

当然我们也可以将减少后的数据集解压缩回原来的784维，通过PCA投影逆变换即可。这个操作不会归还原有的数据，因为投影的操作损失了一小部分的信息（5% 以内的variance 被丢弃），但是它会与原数据非常近似。原数据与重建数据（也就是压缩后再解压缩）之间的均方距离称为重建误差（reconstruction error）。

下面的代码将MNIST 数据集压缩到154维，然后使用 inverse_transform() 方法将它解压回784维：

pca = PCA(n_components = 154)

X_reduced = pca.fit_transform(X_train)

X_recovered = pca.inverse_transform(X_reduced)

 

下图展示了原始训练集的几个手写数字（左图），以及对应压缩与解压缩后的数字。我们可以看到仅有小部分的画质丢失，但是数字仍基本完整。

 逆转换的公式如下所示

 

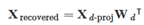
随机化PCA

如果我们设置svd_solver 超参数为“randomized”，则sk-learn会使用一个随机算法，称为Randomized PCA，它会非常快速地找到前d个主成成分的近似值。它的计算复杂度为O(m × d²) + O(d³)，而原始的full SVD计算复杂度为O(m × n²) + O(n³) 。所以这个方法比full SVD要快得多，特别是在d远小于n的情况下。

rnd_pca = PCA(n_components=154, svd_solver="randomized")

X_reduced = rnd_pca.fit_transform(X_train)

 

默认情况下，svd_solver 设置为“auto”：如果m或者n大于500，且d小于m或 n 的80%，则sk-learn会自动使用PCA算法，否则使用full SVD。如果希望强制sk-learn使用full SVD，则我们可以设置 svd_solver 超参数为“full”。

 

增量PCA

前面实现PCA的方法有一个问题，它需要将整个训练集放入内存，才能保证算法运行。不过幸运的是，增量PCA（Incremental PCA，IPCA）算法已被开发。它允许我们将训练集分割成多个小的batch，每次向IPCA算法输入一个batch数据集。这个在大型训练集和在线PCA（也就是一直有新数据实例过来）中非常有帮助。

下面的代码将MNIST数据集分割成100个mini-batch（使用Numpy的array_split() 方法），并将它们输入到sk-learn 的IncrementalPCA类中，将MNIST数据集的维度减少到154维。需要注意的是，我们必须要为每个mini-batch调用一次partial_fit() 方法，而不是在整个训练集上调用fit() 方法：

from sklearn.decomposition import IncrementalPCA

n_batches = 100
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_train, n_batches):
    inc_pca.partial_fit(X_batch)

X_reduced = inc_pca.transform(X_train)

 

或者，我们也可以使用NumPy的memmap类，它可以让我们在一个位于磁盘上的二进制文件中操作一个非常大的数组，看起来就像它全部在内存里一样。这个类仅载入它需要的数据到内存。由于IncrementalPCA类每次仅适用一小部分数组数据，所以内存的使用是可以控制的。这样可以让我们直接调用fit() 方法称为可能，如下代码所示：

X_mm = np.memmap(filename, dtype="float32", mode="readonly", shape=(m, n))

batch_size = m // n_batches
inc_pca = IncrementalPCA(n_components=154, batch_size=batch_size)
inc_pca.fit(X_mm)

 

核化PCA

在SVM中我们介绍过核方法，一个数学技巧，用于将数据实例映射到一个非常高维的空间（称为特征空间），以让SVM处理非线性分类与回归问题。而在高维特征空间中的一个线性决策边界，对应的是一个在原空间里复杂非线性的决策边界。

同样的方法也可以应用在PCA中，可以让PCA执行一个复杂的非线性投影，以实现降维。这个称为核化PCA（Kernel PCA，kPCA）。它一般可以在投影后仍很好地保留原数据的簇（clusters），或者有时候甚至展开一个接近弯曲的流形数据集。

下面的代码使用sk-learn的KernelPCA类执行kPCA，使用RBF核：

from sklearn.decomposition import KernelPCA

rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.04)
X_reduced = rbf_pca.fit_transform(X)

 

下图展示的瑞士卷分别使用线性核（等同于仅使用PCA类），RBF核和sigmoid核进行降维到2维空间后的图：

 

选择核并调优超参数

由于kPCA是一个非监督学习，所以没有一个很明显的性能衡量方式来帮助我们选择一个最好的核以及超参数的值。也就是说，降维一般是监督学习任务（如分类）中的一个准备阶段，所以我们可以使用网格搜索，用于选择使得任务表现最好的核以及超参数，。

下面的代码创建了一个pipeline，包含两个步骤。第一个使用kPCA将维度降为2，然后使用逻辑回归做分类。第二个步骤使用GridSearchCV为kPCA找到最佳的核以及gama值，以使得分类准确性最高。

 

from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline

clf = Pipeline([
        ("kpca", KernelPCA(n_components=2)),
        ("log_reg", LogisticRegression())
    ])

param_grid = [{
        "kpca__gamma": np.linspace(0.03, 0.05, 10),
        "kpca__kernel": ["rbf", "sigmoid"]
    }]

grid_search = GridSearchCV(clf, param_grid, cv=3)
grid_search.fit(X, y)

最佳的核以及超参数之后可以通过best_params_ 变量获取：

print(grid_search.best_params_)

{'kpca__gamma': 0.043333333333333335, 'kpca__kernel': 'rbf'}

 

还有另一个方法，这次是完全非监督的，是选择令重建误差（reconstruction error）最小的核与超参数。需要注意的是，重建并不像线性PCA那样简单。下图展示了原始的瑞士卷3D数据集（左上图）以及在执行kPCA（使用RBF核）后的2D数据集（右上图）。归因于核方法，这个转换在数学上等同于使用特征映射φ将训练集映射到了一个无线维特征空间中（右下图），然后使用线性PCA将转换后的训练集投影到一个2D空间。

 

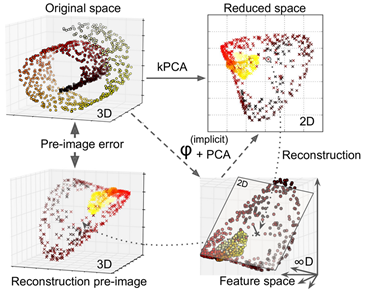
需要注意的是，对于给定一个在已降维空间里的数据实例来说，如果我们可以对它进行反转线性PCA的步骤，那这个重建后的点会位于一个特征空间中，但不是原空间中（例如图中由X表示的那个点）。因为特征空间是无限维的，我们无法计算重建后的点，并因此无法计算出真正的重建误差。不过幸运的是，我们可以在原始空间中找到一个点，它对应于重构后的点（不是完全对应，而是接近）。这个点称为重构原相（reconstruction pre-image）。一旦我们有了这个原像后，我们就可以衡量它到原始数据的平方距离。我们接着就可以选择使得重构原像误差最小的核与超参数。

那如何执行这个重建呢？一个解决方法是训练一个监督回归模型，使用投影后的实例作为训练集，原始实例为labels。sk-learn中，如果设置了fit_inverse_transform=True，则sk-learn会自动做这个步骤，如下所示：

rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.0433,
                    fit_inverse_transform=True)
X_reduced = rbf_pca.fit_transform(X)
X_preimage = rbf_pca.inverse_transform(X_reduced)

 

需要注意的是，默认情况下，fit_inverse_transform=False与KernalPCA没有inverse_transform()方法。这个方法仅在设置fit_inverse_transform=True后才会被创建。

接着可以计算重构原像误差：

from sklearn.metrics import mean_squared_error
mean_squared_error(X, X_preimage)

 

现在我们就可以使用网格搜索与交叉验证用于找到使得这个误差最小的核与超参数。