降维（一）维度灾难与降维主要方法

降维

在很多机器学习问题中，训练集中的每条数据经常伴随着上千、甚至上万个特征。要处理这所有的特征的话，不仅会让训练非常缓慢，还会极大增加搜寻良好解决方案的困难。这个问题就是我们常说的维度灾难。

不过值得庆幸的是，在实际问题中，经常可以极大地减少特征的数目，将棘手的问题转变为容易处理的问题。例如，以MNIST图片数据集为例：在图片边框附近的像素点基本都是白色，所以我们完全可以从训练集中剔除掉这些像素点，并且不损失任何信息。并且，两个相邻像素点之间一般都是高度相关的：如果我们将它们合并成单个像素点（例如，取两个像素点强度的平均值），我们也不会丢失太多信息。

需要注意的是，减少维度实际是会让一些信息丢失（与压缩图片为JPEG会降低它的画质同理）。所以即使它能加速训练，它也可能会让我们系统的表现稍差。同时它也会让我们的管道稍些复杂而因此维护更难。所以如果训练并不是特别慢，则我们应该优先尝试使用原数据集进行训练，而不是考虑用降维。在某些情况下，减少训练数据的维度可能会过滤掉一些不必要的细节，并因此获取更高的性能。但是，一般情况下并不会，它仅是加速训练。

除了加速训练，降维也对数据可视化非常有用。将维度的数量减少到2（或3）个，可以让我们给高维训练集画出一个精简的图，并且一般可以提供我们一些重要的信息（例如可以直接看到一些模式，如簇）。除此之外，数据可视化也可以在与其他非数据科学家人员沟通时非常重要。

在这章我们会讨论维度灾难，并看一下高维空间内具体会发生些什么。接着我们会引入两个主要的降维方法（projection与Manifold Learning），并最后介绍3个最流行的降维技术：PCA，核PCA以及LLE。

 

维度灾难

由于我们生活在并且习惯于3维世界，所以当我们尝试想象高维空间时，一般很难有个直观的感受。即使是一个4D的超立方体，在我们脑海中也很难进行想象，更不用说200-维的椭球体在1000-维空间的弯曲的样子了。下图是0D（0维）到4D超平面的一个示例：

 

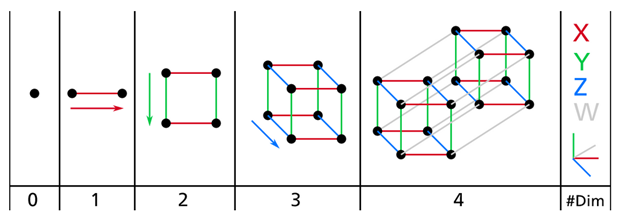
在高维空间中，很多事情的行为都会非常不一样。例如，假设我们在一个单元正方形（1x1正方形）中选择一个随机点，则此点仅有40%的概率与边框的距离小于0.001（也就是说，一个随机点不太可能非常靠近某个维度）。但是在一个10000维的单元超立方体中，这个概率要高于99.999999%。大部分在高维超平面中的点都非常接近于边界。

还有一个更麻烦的差异：假设我们在一个单元正方形中随机选取两个点，这两个点的平均距离约为0.52。如果我们在一个3D立方体中随机选择两个点，则平均距离大约为0.66。但是如果我们在1000000维超立方体中随机选择两个点的话，它们的平均距离大约为408.25（约为1000000/6的平方根 ） 。这是一个很反直觉的现象：为什么两个点都在同样的单元超平面中，但是距离可以离的这么远？当然这是由于在高维中有足够多的空间导致了。所以这样导致的结果就是：高维数据集中的数据点可能会非常稀疏（或离散）。大多数训练实例可能相互之间离的都非常远，导致预测性能相对于低维数据集来说会更不可靠，因为它们基于的是更大的外推法（extrapolations）。简单地说，训练集的维度越高，过拟合的风险越大。

理论上来说，一个解决维度灾难的办法是增加训练集的大小，以达到一个足够训练数据条目的量。但遗憾的是，实际上所需增长的训练数据条目量是根据维度数呈指数级别增长的。对于仅仅100个特征来说（这已经远小于MINST问题的维度了），我们需要的训练数据条目数都已经超过我们平常的认知数了。

 

降维的主要方法

在我们深入了解特定降维算法之前，我们先看一下两个主要的降维方法：投影（projecting）与流形学习（Manifold Learning）。

 

Projection

在大多数是实际问题中，训练数据并不会跨所有维度均匀分布。很多特征几乎是不变的，而其他特征是高度相关的（例如之前提到过的MNIST）。在这些情况下，数据集中所有的训练实例都可以放在（或者接近于）一个更低维的子空间中。举个例子，下图中我们可以看到一个3维数据集，在投影后可以由圆环表示：

 

 

可以注意到所有训练实例都接近于一个平面：这个是3D空间中的一个2D子空间。如果我们将所有训练实例垂直投影到这个子空间，则可以得到一个新的2D数据集，如下所示：

 

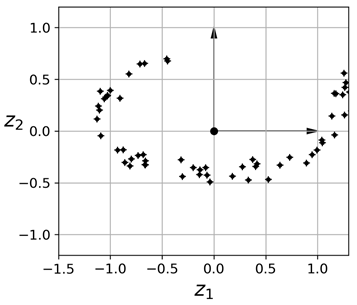
需要注意的是，坐标轴对应的是两个新特征z1和z2（投影在这个平面上的坐标）。

不过，投影并不总是最好的降维方法。在很多情况下，子空间可能弯曲和旋转，例如著名的瑞士卷数据集：

 

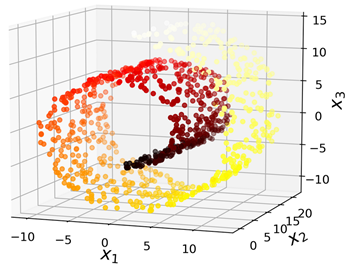
如果简单的将它们投影到一个平面（例如，直接丢弃x3）则会将不同层的数据挤压到一起，如下左图所示。不过我们真正希望的是将这个瑞士卷展开，而获取一个2D数据集，如右图所示：

 

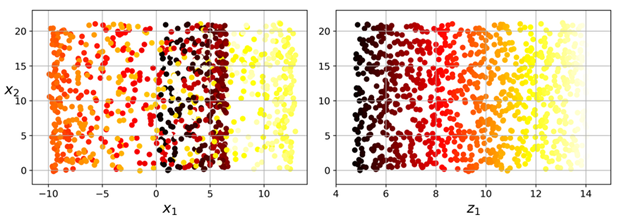
流形学习（Manifold Learning）

瑞士卷数据集是一个2D流形的例子。简单地说，一个2D流形是一个2D的形状，可以弯曲并旋转到一个更高的空间中。更普遍地说，一个d-维的流形是一个n-维空间里的一部分（d < n），在本地类似于一个d-维的超平面。在这个瑞士卷例子中，d=2，n=3：它在本地类似一个2D平面，但是是在3维里卷成。

许多降维算法的方式是在训练实例上做流形建模，这个称为流形学习（Manifold Learning）。它基于的是流形假设（manifold assumption），也成为流形假说（manifold hypothesis）。它假设真实世界中大多数的高维数据集接近于一个非常低维的流形。从经验来看，经常可以观察到这个现象。

再看一下MNIST数据集：所有的手写数字图片都有一些相似的地方。它们由连接的线构成、边框是白色、并且它们或多或少都处于中心。如果我们随机产生一张图片，仅仅使用它们其中的一小部分也会让它看起来像一个手写数字。换句话说，我们若是想要生成一张手写图，所需的维度远小于原图的维度。

流形假说经常伴随着另一个假说：如果目标任务（例如分类或是回归）以低维空间的流形表示的话，会使得任务更简单。例如，在下图第一行中，瑞士卷被分成两个类：在3D空间中（左图），决策边界会有些复杂，但是在2D展开后的流形空间中（右图），决策边界非常简答，就是一条直线。

 

不过，这种隐形假说并不总是成立的。例如在上图的下半部分，决策边界在x1=5。这个决策边界在原3D空间内非常简单（就是一个垂直平面），但是在展开后的流形中看起来更复杂一些（包含四条独立的线段）。

简而言之，在训练模型之间对训练集进行降维通常可以加速训练，但它可能并不是一直都引入到一个更好、或更简单的解决方案；它全部取决于数据集。

现在我们已经了解了维度灾难，并且可以使用什么样的降维算法来对抗此问题。之后我们会介绍一些最常见的算法。