决策树（二）决策树回归

回归

决策树也可以用于执行回归任务。我们首先用sk-learn的DecisionTreeRegressor类构造一颗回归决策树，并在一个带噪声的二次方数据集上进行训练，指定max_depth=2：

import numpy as np

# Quadratic training set + noise
np.random.seed(42)
m = 200

X = np.random.rand(m, 1)
y = 4 * (X - 0.5) ** 2
y = y + np.random.randn(m, 1) / 10

from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg.fit(X, y)

 

下图是这棵树的结果：

 

 

这棵树看起来与之前构造的分类树类似。主要的区别是：在每个节点中，预测的不是一个类别，而是一个值。例如，假设我们想为一个新的实例x1=0.6做预测。我们会先从根节点遍历树，最终到达预测value=0.111的叶子节点。这个预测值是与这个叶子节点关联的110条训练数据的平均值，并且它在这110条数据上的均方误差等于0.015。

这个模型的预测在如下左图中进行表示。如果设置max_depth=3，则得到如下右图。需要注意的是：每个区域的预测值，都是当前区域中所有目标值的平均值。算法在分割区域时，会以一种让大部分训练数据尽可能地靠近预测的值的方式进行分割。

 

CART算法在这与之前提到的原理基本类似，除了在分割训练集时，之前是找到一种分割让不纯度最小；现在是找到一种分割让MSE最小。下面是算法要最小化的损失函数：

 

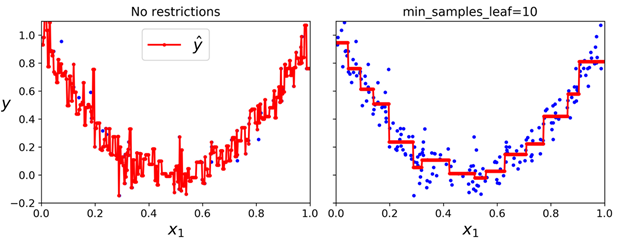
与分类任务一样，在处理回归任务时，决策树也会倾向于过拟合。如果没有任何的正则（例如使用的是默认的参数），则我们会得到下面左图的（在训练集上）预测的结果。很明显这些预测在训练集上是过拟合的。在仅设置min_samples_leaf=10 后，我们可以得到一个更合理的模型，如下右图所示：

 

不稳定性

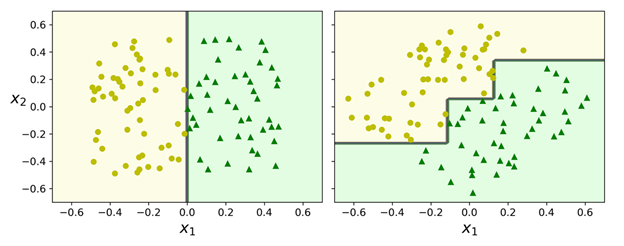
到目前为止，我们已经了解了决策树的基本特点：易于理解与表示、上手简单并且功能强大。不过，它们仍有一些局限性。首先，大家可能已经注意到过，决策树喜欢直角的决策边界（所有的分割都是与一个轴垂直的），这个会让决策树对训练数据的旋转非常敏感。例如，下图是一个简单的线性可分数据集：在左边，一个决策树可以很容易地将它们分割；但是对于右边的图，在数据集旋转了45°之后，决策边界看起来复杂了一些（但是这种复杂很没有必要）。尽管两个决策树都能完美地拟合训练集，但是很大可能右边的模型的泛化性能不会太好。其中一个缓解这个问题的办法是使用主成成分分析（Principal Component Analysis），使用它后，基本可以让训练数据有一个更好的方向（角度）。

 

不过在决策树中最常见也最主要的问题是：它们对训练集中的微小变化都非常敏感。例如，假设我们仅仅是从iris训练集中移除掉最宽的Iris versicolor（这条数据的length=4.8 cm，width=1.8cm） ，然后重新训练一个新的决策树，我们可能会得到下面的模型：

 

从这模型里我们可以看到，它与之前训练的决策树模型差别非常大。不过实际上由于sk-learn是随机的（它会随机选择一组特征，在每个节点中进行评估），所以即使是在同样的训练数据上，每次训练出来的模型可能都是差别比较大的（除非设置了random_state 超参数）。

随机森林可以限制这种不稳定性，通过在多个树上取平均预测，我们之后会介绍。